Სარჩევი
ამ გაკვეთილზე ჩვენ განვიხილავთ, თუ როგორ უნდა გავაკეთოთ დისპერსიული ანალიზი Excel-ში და რა ფორმულები გამოვიყენოთ ნიმუშისა და პოპულაციის დისპერსიის მოსაძებნად.
ვარიაცია ერთ-ერთი ყველაზე სასარგებლოა. ინსტრუმენტები ალბათობის თეორიასა და სტატისტიკაში. მეცნიერებაში ის აღწერს, თუ რამდენად დაშორებულია მონაცემთა ნაკრების თითოეული რიცხვი საშუალოდან. პრაქტიკაში, ის ხშირად აჩვენებს, თუ რამდენად იცვლება რაღაც. მაგალითად, ეკვატორთან ახლოს ტემპერატურას ნაკლები განსხვავება აქვს, ვიდრე სხვა კლიმატურ ზონებში. ამ სტატიაში ჩვენ გავაანალიზებთ Excel-ში დისპერსიის გამოთვლის სხვადასხვა მეთოდს.
რა არის ვარიაცია?
ვარიანსი არის ცვალებადობის საზომი მონაცემთა ნაკრები, რომელიც მიუთითებს, თუ რამდენად შორს არის გავრცელებული სხვადასხვა მნიშვნელობები. მათემატიკურად, ის განისაზღვრება, როგორც საშუალოდან კვადრატული სხვაობების საშუალო.
იმისათვის, რომ უკეთ გავიგოთ, რას ითვლით რეალურად დისპერსიით, გთხოვთ, გაითვალისწინოთ ეს მარტივი მაგალითი.
დავუშვათ, რომ არის 5. ვეფხვები თქვენს ადგილობრივ ზოოპარკში, რომლებიც არიან 14, 10, 8, 6 და 2 წლის.
სხვაობების საპოვნელად მიჰყევით ამ მარტივ ნაბიჯებს:
- გამოთვალეთ საშუალო (მარტივი საშუალო) ხუთი რიცხვიდან:
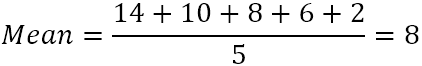
- თითოეულ რიცხვს გამოაკლეთ საშუალო განსხვავებების საპოვნელად. ამის ვიზუალიზაციისთვის, მოდით გამოვსახოთ განსხვავებები დიაგრამაზე:
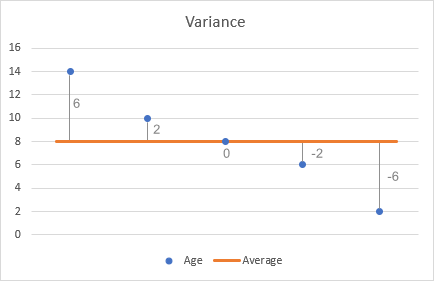
- თითოეული სხვაობის კვადრატში.
- დაამუშავეთ კვადრატული სხვაობების საშუალო მნიშვნელობა.
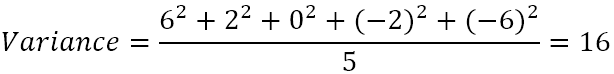
მაშ ასე, განსხვავება არის 16. მაგრამ რას ნიშნავს ეს რიცხვირეალურად ნიშნავს?
სინამდვილეში, დისპერსიას მხოლოდ ძალიან ზოგად წარმოდგენას გაძლევთ მონაცემთა ნაკრების დისპერსიის შესახებ. მნიშვნელობა 0 ნიშნავს, რომ არ არსებობს ცვალებადობა, ანუ მონაცემთა ნაკრების ყველა რიცხვი ერთნაირია. რაც უფრო დიდია რიცხვი, მით უფრო გავრცელებულია მონაცემები.
ეს მაგალითი არის პოპულაციის ცვალებადობისთვის (ანუ 5 ვეფხვი არის მთელი ჯგუფი, რომელიც თქვენ გაინტერესებთ). თუ თქვენი მონაცემები შერჩეულია უფრო დიდი პოპულაციისგან, მაშინ თქვენ უნდა გამოთვალოთ ნიმუშის ვარიაცია ოდნავ განსხვავებული ფორმულის გამოყენებით.
როგორ გამოვთვალოთ დისპერსია Excel-ში
არსებობს 6 ჩაშენებული ფუნქცია დისპერსიის გასაკეთებლად Excel-ში: VAR, VAR.S, VARP, VAR.P, VARA და VARPA.
დისპერსიის ფორმულის თქვენი არჩევანი განისაზღვრება შემდეგი ფაქტორებით:
- Excel-ის ვერსია, რომელსაც იყენებთ.
- მიხედავთ თუ არა ნიმუშის ან პოპულაციის დისპერსიას.
- გსურთ შეაფასოთ თუ უგულებელყოთ ტექსტი და ლოგიკური მნიშვნელობები.
Excel ვარიაციის ფუნქციები
ქვემოთ მოცემული ცხრილი გთავაზობთ Excel-ში არსებული ვარიაციის ფუნქციების მიმოხილვას, რათა დაგეხმაროთ აირჩიოთ ფორმულა, რომელიც საუკეთესოდ შეეფერება თქვენს საჭიროებებს.
| სახელი | Excel-ის ვერსია | მონაცემთა ტიპი | ტექსტი და ლოგიკა |
| VAR | 2000 - 2019 | ნიმუში | იგნორირებული |
| VAR.S | 2010 - 2019 | ნიმუში | იგნორირებული |
| VARA | 2000 -2019 | ნიმუში | შეფასებული |
| VARP | 2000 - 2019 | მოსახლეობა | იგნორირებული |
| VAR.P | 2010 - 2019 | მოსახლეობა | იგნორირებული |
| VARPA | 2000 - 2019 | მოსახლეობა | შეფასებული |
VAR.S vs. VARA და VAR.P VARPA-ს წინააღმდეგ
VARA და VARPA განსხვავდებიან სხვა დისპერსიული ფუნქციებისგან მხოლოდ იმით, რომ ამუშავებენ ლოგიკურ და ტექსტურ მნიშვნელობებს მითითებებში. შემდეგი ცხრილი ასახავს შეჯამებას, თუ როგორ ფასდება რიცხვებისა და ლოგიკური მნიშვნელობების ტექსტური წარმოდგენები.
| არგუმენტის ტიპი | VAR, VAR.S, VARP, VAR.P | VARA & amp; VARPA |
| ლოგიკური მნიშვნელობები მასივებში და მითითებებში | იგნორირებულია | შეფასებული (TRUE=1, FALSE=0) |
| ციფრების ტექსტური წარმოდგენები მასივებში და მითითებებში | იგნორირებულია | შეფასებულია როგორც ნული |
| ლოგიკური პირდაპირ არგუმენტებში აკრეფილი რიცხვების მნიშვნელობები და ტექსტური წარმოდგენები | შეფასებული (TRUE=1, FALSE=0) | |
| ცარიელი უჯრედები | იგნორირებული | |
როგორ გამოვთვალოთ ნიმუშის განსხვავება Excel-ში
A ნიმუში არის მთელი პოპულაციისგან ამოღებული მონაცემების ნაკრები. და ნიმუშიდან გამოთვლილ დისპერსიას ეწოდება მაგალითის ვარიაცია .
მაგალითად, თუ გსურთ იცოდეთ როგორ იცვლება ადამიანების სიმაღლეები, თქვენთვის ტექნიკურად შეუძლებელი იქნება თითოეული ადამიანის გაზომვა დედამიწა.გამოსავალი არის აიღოთ პოპულაციის ნიმუში, ვთქვათ 1000 ადამიანი და შეაფასოთ მთლიანი პოპულაციის სიმაღლეები ამ ნიმუშის საფუძველზე.
საარჩევნო ვარიაცია გამოითვლება ამ ფორმულით:
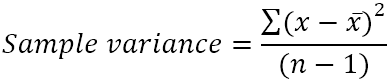
სად:
- x̄ არის ნიმუშის მნიშვნელობების საშუალო (მარტივი საშუალო).
- n არის ნიმუშის ზომა, ანუ მნიშვნელობების რაოდენობა ნიმუში.
Excel-ში ნიმუშის დისპერსიის საპოვნელად არის 3 ფუნქცია: VAR, VAR.S და VARA.
VAR ფუნქცია Excel-ში
ეს არის უძველესი Excel ფუნქცია ნიმუშის საფუძველზე დისპერსიის შესაფასებლად. VAR ფუნქცია ხელმისაწვდომია Excel 2000-დან 2019 წლამდე ყველა ვერსიაში.
VAR(number1, [number2],…)შენიშვნა. Excel 2010-ში VAR ფუნქცია შეიცვალა VAR.S-ით, რომელიც უზრუნველყოფს გაუმჯობესებულ სიზუსტეს. მიუხედავად იმისა, რომ VAR კვლავ ხელმისაწვდომია უკანა თავსებადობისთვის, რეკომენდებულია VAR.S-ის გამოყენება Excel-ის მიმდინარე ვერსიებში.
VAR.S ფუნქცია Excel-ში
ეს არის Excel-ის თანამედროვე ანალოგი. VAR ფუნქცია. გამოიყენეთ VAR.S ფუნქცია Excel 2010-ში და შემდეგში ნიმუშის დისპერსიის საპოვნელად.
VAR.S(number1, [number2], …)VARA ფუნქცია Excel-ში
Excel VARA ფუნქცია აბრუნებს დისპერსიის ნიმუში დაფუძნებულია რიცხვების, ტექსტისა და ლოგიკური მნიშვნელობების ერთობლიობაზე, როგორც ეს ნაჩვენებია ამ ცხრილში.
VARA(მნიშვნელობა1, [მნიშვნელობა2],…)დისპერსიის ნიმუშის ფორმულა Excel-ში
როდესაც მუშაობთ მონაცემთა რიცხვითი ნაკრები, რომელიც შეგიძლიათ გამოიყენოთ ნებისმიერი ზემოაღნიშნული ფუნქცია ნიმუშის დისპერსიის გამოსათვლელადExcel-ში.
მაგალითად ვიპოვოთ 6 ელემენტისგან შემდგარი ნიმუშის (B2:B7) განსხვავება. ამისთვის შეგიძლიათ გამოიყენოთ ქვემოთ მოყვანილი ერთ-ერთი ფორმულა:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
როგორც ნაჩვენებია ეკრანის სურათზე, ყველა ფორმულა აბრუნებს იგივე შედეგი (დამრგვალებულია 2 ათწილადამდე):
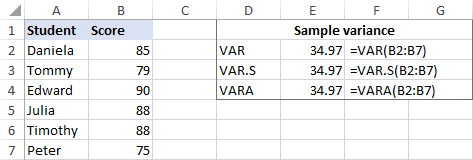
შედეგის შესამოწმებლად, მოდით ხელით გავაკეთოთ var-ის გამოთვლა:
- იპოვეთ საშუალო გამოყენებით AVERAGE ფუნქცია:
=AVERAGE(B2:B7)საშუალო მიდის ნებისმიერ ცარიელ უჯრედზე, ვთქვათ B8.
- გამოაკლეთ საშუალო ნიმუშში თითოეულ რიცხვს:
=B2-$B$8განსხვავებები მიდის C სვეტში, დაწყებული C2-დან.
Იხილეთ ასევე: Excel SORTBY ფუნქცია - მორგებული დალაგება ფორმულით - თითო სხვაობა გამოყავით კვადრატში და ჩადეთ შედეგები D სვეტში, დაწყებული D2-დან:
=C2^2 - დააკრიფეთ კვადრატული განსხვავებები და შედეგი გაყავით რიცხვზე ელემენტი ნიმუშში მინუს 1:
=SUM(D2:D7)/(6-1)
როგორც ხედავთ, ჩვენი ხელით var გაანგარიშების შედეგი ზუსტად იგივეა, რაც Excel-ის ჩაშენებული ფუნქციებით დაბრუნებული რიცხვი:
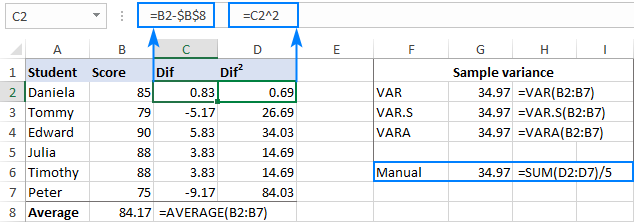
თუ თქვენი მონაცემთა ნაკრები შეიცავს Boolean და/ან text მნიშვნელობებს, VARA ფუნქცია დააბრუნებს განსხვავებულ შედეგს. მიზეზი არის ის, რომ VAR და VAR.S იგნორირებას უკეთებენ სხვა მნიშვნელობებს, გარდა რიცხვებისა, მითითებებში, ხოლო VARA აფასებს ტექსტის მნიშვნელობებს ნულებად, TRUE-ად 1-ად და FALSE-ად, როგორც 0-ად. ამიტომ, გთხოვთ, ყურადღებით აირჩიოთ დისპერსიის ფუნქცია თქვენი გამოთვლებისთვის, იმისდა მიხედვით, თუ რამდენად გსურთ ტექსტის და ლოგიკის დამუშავება ან იგნორირება.
როგორგამოთვალეთ პოპულაციის ცვალებადობა Excel-ში
პოპულაცია არის მოცემული ჯგუფის ყველა წევრი, ანუ ყველა დაკვირვება კვლევის სფეროში. პოპულაციის ვარიაცია აღწერს, თუ როგორ მიუთითებს მონაცემები მთელში პოპულაცია განაწილებულია.
პოპულაციის დისპერსიის ნახვა შეგიძლიათ ამ ფორმულით:
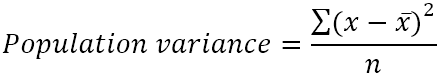
სად:
- x̄ არის პოპულაციის საშუალო.
- n არის პოპულაციის ზომა, ანუ მნიშვნელობების საერთო რაოდენობა პოპულაციაში.
Excel-ში პოპულაციის დისპერსიის გამოსათვლელად 3 ფუნქციაა: VARP, VAR .P და VARPA.
VARP ფუნქცია Excel-ში
Excel VARP ფუნქცია აბრუნებს პოპულაციის დისპერსიას რიცხვების მთელი ნაკრების საფუძველზე. ის ხელმისაწვდომია Excel 2000-დან 2019 წლამდე ყველა ვერსიაში.
VARP(number1, [number2],…)შენიშვნა. Excel 2010-ში VARP შეიცვალა VAR.P-ით, მაგრამ მაინც ინახება უკანა თავსებადობისთვის. რეკომენდებულია VAR.P-ის გამოყენება Excel-ის მიმდინარე ვერსიებში, რადგან არ არსებობს გარანტია, რომ VARP ფუნქცია ხელმისაწვდომი იქნება Excel-ის მომავალ ვერსიებში.
VAR.P ფუნქცია Excel-ში
ეს არის VARP ფუნქციის გაუმჯობესებული ვერსია, რომელიც ხელმისაწვდომია Excel 2010-ში და შემდეგში.
VAR.P(number1, [number2], …)VARPA ფუნქცია Excel-ში
VARPA ფუნქცია ითვლის დისპერსიას პოპულაცია, რომელიც დაფუძნებულია რიცხვების, ტექსტისა და ლოგიკური მნიშვნელობების მთელ კომპლექტზე. ის ხელმისაწვდომია Excel 2000-ის ყველა ვერსიაში 2019 წლამდე.
VARA(მნიშვნელობა1,[მნიშვნელობა2], …)პოპულაციის დისპერსიის ფორმულა Excel-ში
ვარის გამოთვლის ნიმუშის მაგალითში, ჩვენ ვიპოვეთ 5 გამოცდის ქულის დისპერსიას, თუ ვივარაუდებთ, რომ ეს ქულები შერჩეული იყო სტუდენტების უფრო დიდი ჯგუფიდან. თუ თქვენ შეაგროვებთ მონაცემებს ჯგუფის ყველა სტუდენტის შესახებ, ეს მონაცემები წარმოადგენს მთელ პოპულაციას და თქვენ გამოთვლით პოპულაციის ვარიაციას ზემოაღნიშნული ფუნქციების გამოყენებით.
ვთქვათ, გვაქვს ჯგუფის გამოცდის ქულები. 10 სტუდენტი (B2:B11). ქულები შეადგენს მთელ პოპულაციას, ამიტომ ჩვენ გავაკეთებთ ვარიაციას ამ ფორმულებით:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
და ყველა ფორმულა დააბრუნებს იდენტური შედეგი:
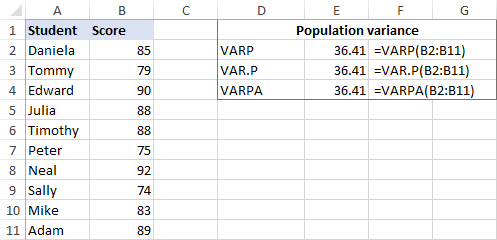
იმისათვის, რომ დარწმუნდეთ, რომ Excel-მა სწორად შეასრულა ვარიაცია, შეგიძლიათ შეამოწმოთ ის ხელით var-ის გამოთვლის ფორმულით, რომელიც ნაჩვენებია ქვემოთ მოცემულ ეკრანის სურათზე:

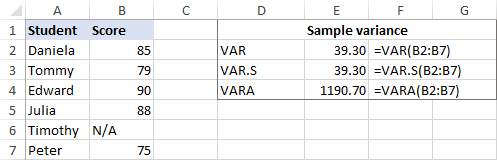
თუ ზოგიერთი სტუდენტი არ გავიდა გამოცდაზე და ქულის ნომრის ნაცვლად აქვს N/A, VARPA ფუნქცია სხვა შედეგს დააბრუნებს. მიზეზი ის არის, რომ VARPA აფასებს ტექსტის მნიშვნელობებს ნულებად, ხოლო VARP და VAR.P უგულებელყოფენ ტექსტს და ლოგიკურ მნიშვნელობებს მითითებებში. იხილეთ VAR.P vs. VARPA სრული დეტალებისთვის.

ვარიანტობის ფორმულა Excel-ში - გამოყენების შენიშვნები
Excel-ში დისპერსიული ანალიზის სწორად გასაკეთებლად, გთხოვთ, მიჰყვეთ ეს მარტივი წესები:
- მოაწოდეთ არგუმენტები მნიშვნელობების, მასივების ან უჯრედების მითითების სახით.
- Excel 2007-ში და შემდეგში, შეგიძლიათ მიაწოდოთ 255-მდე არგუმენტი, რომელიც შეესაბამებანიმუში ან პოპულაცია; Excel 2003 და უფრო ძველი - 30-მდე არგუმენტი.
- მინიშნებებში მხოლოდ ნომრების შესაფასებლად, ცარიელი უჯრედების, ტექსტისა და ლოგიკური მნიშვნელობების იგნორირება, გამოიყენეთ VAR ან VAR.S ფუნქცია გამოთვალეთ ნიმუშის ვარიაცია და VARP ან VAR.P პოპულაციის დისპერსიის საპოვნელად.
- ლოგიკური და ტექსტის მნიშვნელობების შესაფასებლად მითითებებში გამოიყენეთ VARA ან VARPA ფუნქცია.
- მიაწოდეთ მინიმუმ ორი რიცხვითი მნიშვნელობა ნიმუშის დისპერსიის ფორმულას და მინიმუმ ერთი რიცხვითი მნიშვნელობა პოპულაციის დისპერსიის ფორმულას Excel-ში, წინააღმდეგ შემთხვევაში #DIV/0! ჩნდება შეცდომა.
- არგუმენტები, რომლებიც შეიცავს ტექსტს, რომლის ინტერპრეტაცია შეუძლებელია რიცხვებად, იწვევს #VALUE! შეცდომები.
ვარიანსი Excel-ში სტანდარტული გადახრის წინააღმდეგ
ვარიანტობა უდავოდ სასარგებლო კონცეფციაა მეცნიერებაში, მაგრამ ის იძლევა ძალიან მცირე პრაქტიკულ ინფორმაციას. მაგალითად, ჩვენ ვიპოვეთ ვეფხვების პოპულაციის ასაკი ადგილობრივ ზოოპარკში და გამოვთვალეთ განსხვავება, რომელიც უდრის 16-ს. საკითხავია - როგორ შეგვიძლია რეალურად გამოვიყენოთ ეს რიცხვი? სტანდარტული გადახრა, რომელიც ბევრად უკეთესი საზომია მონაცემთა ნაკრების ცვალებადობის ოდენობის.
სტანდარტული გადახრა გამოითვლება, როგორც ვარიაციის კვადრატული ფესვი. მაშ ასე, ვიღებთ 16-ის კვადრატულ ფესვს და ვიღებთ 4-ის სტანდარტულ გადახრას.
საშუალოსთან ერთად, სტანდარტული გადახრა შეიძლება გითხრათ რამდენი წლისაა ვეფხვების უმეტესობა. მაგალითად, თუსაშუალო არის 8 და სტანდარტული გადახრა არის 4, ზოოპარკში ვეფხვების უმრავლესობა 4 წლამდე (8 - 4) და 12 წლამდე (8 + 4).
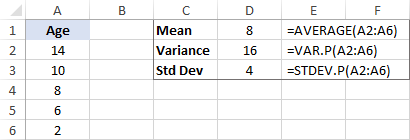
Microsoft Excel-ს აქვს სპეციალური ფუნქციები ნიმუშისა და პოპულაციის სტანდარტული გადახრის გამოსათვლელად. ყველა ფუნქციის დეტალური ახსნა შეგიძლიათ იხილოთ ამ სახელმძღვანელოში: როგორ გამოვთვალოთ სტანდარტული გადახრა Excel-ში.
აი, როგორ გავაკეთოთ ვარიაცია Excel-ში. ამ სახელმძღვანელოში განხილული ფორმულების უფრო დეტალურად დასათვალიერებლად, შეგიძლიათ ჩამოტვირთოთ ჩვენი სამუშაო წიგნის ნიმუში ამ პოსტის ბოლოს. მადლობას გიხდით წაკითხვისთვის და იმედი მაქვს, რომ მომავალ კვირას გნახავთ ჩვენს ბლოგზე!
სავარჯიშო სამუშაო წიგნი
გამოთვალეთ ვარიაცია Excel-ში - მაგალითები (ფაილი .xlsx)

