Съдържание
В този урок ще разгледаме как да направим дисперсионен анализ в Excel и какви формули да използваме, за да намерим дисперсията на извадка и популация.
Дисперсията е един от най-полезните инструменти в теорията на вероятностите и статистиката. В науката тя описва колко далеч е всяко число в набора от данни от средната стойност. В практиката тя често показва колко се променя нещо. Например температурата в близост до екватора има по-малка дисперсия, отколкото в други климатични зони. В тази статия ще анализираме различни методи за изчисляване на дисперсията в Excel.
Какво е дисперсия?
Отклонение е мярка за променливост на набор от данни, която показва колко далеч са разпръснати различните стойности. Математически тя се определя като средната стойност на квадратичните разлики от средната стойност.
За да разберете по-добре какво всъщност изчислявате с дисперсията, разгледайте този прост пример.
Да предположим, че в местната зоологическа градина има 5 тигъра, които са на 14, 10, 8, 6 и 2 години.
За да откриете отклонение, следвайте тези прости стъпки:
- Изчислете средната стойност (проста средна стойност) на петте числа:
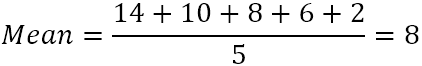
- От всяко число извадете средната стойност, за да откриете разликите. За да визуализираме това, нека нанесем разликите на графиката:
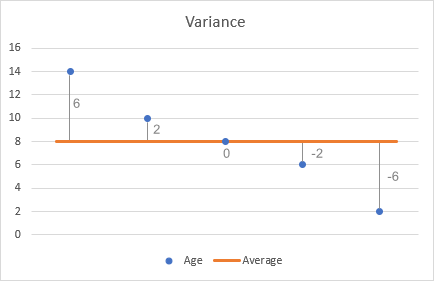
- Изравнете всяка разлика.
- Изчислете средната стойност на квадратните разлики.
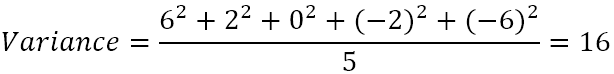
И така, дисперсията е 16. Но какво всъщност означава това число?
Всъщност дисперсията ви дава само много обща представа за разсейването на набора от данни. Стойност 0 означава, че няма дисперсия, т.е. всички числа в набора от данни са еднакви. Колкото по-голямо е числото, толкова по-разпръснати са данните.
Този пример е за дисперсия на популацията (т.е. 5 тигъра са цялата група, която ви интересува). Ако данните ви са подбор от по-голяма популация, трябва да изчислите дисперсията на извадката, като използвате малко по-различна формула.
Как да изчислим дисперсията в Excel
В Excel има 6 вградени функции за дисперсия: VAR, VAR.S, VARP, VAR.P, VARA и VARPA.
Изборът на формулата за дисперсия се определя от следните фактори:
- Версията на Excel, която използвате.
- Дали се изчислява дисперсията на извадката или на популацията.
- Дали искате да оценявате или игнорирате текстови и логически стойности.
Функции за дисперсия на Excel
В таблицата по-долу е представен преглед на наличните в Excel функции за вариране, за да ви помогне да изберете най-подходящата за вашите нужди формула.
| Име | Версия за Excel | Тип данни | Текст и логики |
| VAR | 2000 - 2019 | Образец | Игнориран |
| VAR.S | 2010 - 2019 | Образец | Игнориран |
| VARA | 2000 - 2019 | Образец | Оценен |
| VARP | 2000 - 2019 | Население | Игнориран |
| VAR.P | 2010 - 2019 | Население | Игнориран |
| VARPA | 2000 - 2019 | Население | Оценен |
VAR.S срещу VARA и VAR.P срещу VARPA
VARA и VARPA се различават от другите функции за вариации само по начина, по който обработват логическите и текстовите стойности в препратките. В следващата таблица е представено обобщение на начина, по който се оценяват текстовите представяния на числата и логическите стойности.
| Тип на аргумента | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Логически стойности в масиви и препратки | Игнориран | Оценен (TRUE=1, FALSE=0) |
| Текстово представяне на числа в масиви и препратки | Игнориран | Оценява се като нула |
| Логически стойности и текстови представяния на числа, въведени директно в аргументите | Оценен (TRUE=1, FALSE=0) | |
| Празни клетки | Игнориран | |
Как да изчислим дисперсията на извадката в Excel
A образец е съвкупност от данни, извлечени от цялата популация. А дисперсията, изчислена от извадка, се нарича дисперсия на извадката .
Например, ако искате да разберете как варира височината на хората, би било технически невъзможно да измерите всеки човек на земята. Решението е да вземете извадка от населението, например 1000 души, и да оцените височината на цялото население въз основа на тази извадка.
Дисперсията на извадката се изчислява по тази формула:
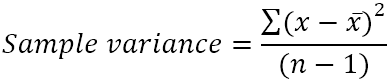
Къде:
- x̄ е средната стойност (проста средна стойност) на стойностите на извадката.
- n е размерът на извадката, т.е. броят на стойностите в извадката.
В Excel има 3 функции за намиране на извадковата дисперсия: VAR, VAR.S и VARA.
Функция VAR в Excel
Това е най-старата функция на Excel за оценка на дисперсията въз основа на извадка. Функцията VAR е налична във всички версии на Excel от 2000 до 2019 г.
VAR(number1, [number2], ...)Забележка: В Excel 2010 функцията VAR беше заменена с VAR.S, която осигурява подобрена точност. Въпреки че VAR все още е налична за обратна съвместимост, се препоръчва да се използва VAR.S в настоящите версии на Excel.
Функция VAR.S в Excel
Това е съвременният аналог на функцията VAR на Excel. Използвайте функцията VAR.S за намиране на дисперсията на извадката в Excel 2010 и по-нови версии.
VAR.S(number1, [number2], ...)Функция VARA в Excel
Функцията VARA на Excel връща примерна дисперсия въз основа на набор от числа, текст и логически стойности, както е показано в тази таблица.
VARA(стойност1, [стойност2], ...)Примерна формула за дисперсия в Excel
Когато работите с цифров набор от данни, можете да използвате някоя от горепосочените функции за изчисляване на извадковата дисперсия в Excel.
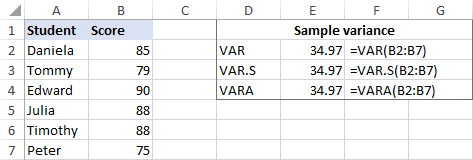
Като пример, нека намерим дисперсията на извадка, състояща се от 6 елемента (B2:B7). За тази цел можете да използвате една от следните формули:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Както е показано на снимката на екрана, всички формули дават един и същ резултат (закръглен до 2 знака след десетичната запетая):
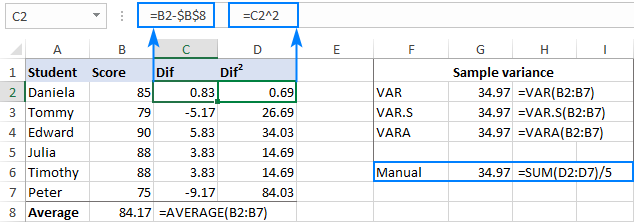
За да проверим резултата, нека направим ръчно изчисление на вар:
- Намерете средната стойност, като използвате функцията AVERAGE:
=СРЕДНА СТОЙНОСТ(B2:B7)Средната стойност отива във всяка празна клетка, например B8.
- Извадете средната стойност от всяко число в извадката:
=B2-$B$8Разликите се пренасят в колона C, като се започва от C2.
- Направете квадрат на всяка разлика и запишете резултатите в колона D, като започнете от D2:
=C2^2 - Съберете квадратните разлики и разделете резултата на броя на елементите в извадката минус 1:
=SUM(D2:D7)/(6-1)
Както можете да видите, резултатът от ръчното изчисление на var е точно същият като числото, върнато от вградените функции на Excel:
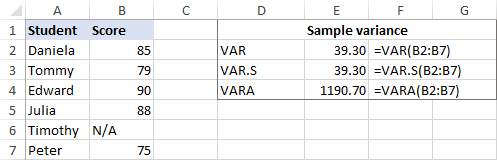
Ако вашият набор от данни съдържа Булеви и/или текст Причината е, че VAR и VAR.S игнорират всякакви стойности, различни от числа, в препратките, докато VARA оценява текстовите стойности като нули, TRUE като 1, а FALSE като 0. Затова внимателно изберете функцията за вариране за вашите изчисления в зависимост от това дали искате да обработвате или игнорирате текст и логически стойности.
Как да изчислим дисперсията на популацията в Excel
Население са всички членове на дадена група, т.е. всички наблюдения в областта на изследването. Дисперсия на населението описва как са разпределени точките с данни в цялата популация.
Дисперсията на популацията може да се намери по тази формула:
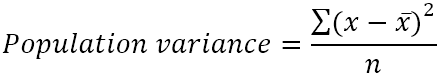
Къде:
- x̄ е средната стойност на популацията.
- n е размерът на популацията, т.е. общият брой стойности в популацията.
В Excel има 3 функции за изчисляване на дисперсията на популацията: VARP, VAR.P и VARPA.
Функция VARP в Excel
Функцията VARP на Excel връща дисперсията на дадена популация въз основа на целия набор от числа. Тя е налична във всички версии на Excel от 2000 до 2019 г.
VARP(number1, [number2], ...)Забележка: В Excel 2010 функцията VARP беше заменена с VAR.P, но все още се запазва за обратна съвместимост. Препоръчва се използването на VAR.P в настоящите версии на Excel, тъй като няма гаранция, че функцията VARP ще бъде налична в бъдещите версии на Excel.
Функция VAR.P в Excel
Това е подобрена версия на функцията VARP, налична в Excel 2010 и по-нови версии.
VAR.P(число1, [число2], ...)Функция VARPA в Excel
Функцията VARPA изчислява дисперсията на дадена популация въз основа на целия набор от числа, текст и логически стойности. Тя е налична във всички версии на Excel от 2000 до 2019 г.
VARA(стойност1, [стойност2], ...)Формула за дисперсия на популацията в Excel
В примерното изчисление на вариацията намерихме дисперсията на 5 изпитни резултата, като предположихме, че тези резултати са подбор от по-голяма група ученици. Ако съберете данни за всички ученици в групата, тези данни ще представляват цялата популация и ще изчислите дисперсията на популацията, като използвате горните функции.
Да кажем, че разполагаме с резултатите от изпитите на група от 10 ученици (B2:B11). Резултатите представляват цялата популация, така че ще направим вариация с тези формули:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
И всички формули ще дадат идентичен резултат:
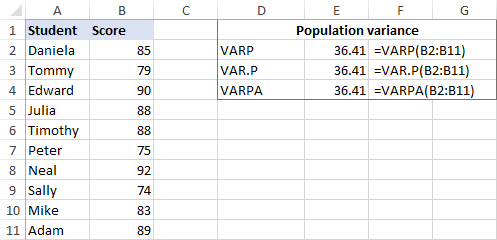
За да се уверите, че Excel е направил правилно вариацията, можете да я проверите с формулата за ръчно изчисляване на вариацията, показана на снимката по-долу:

Ако някои от учениците не са се явили на изпита и вместо номер на резултата имат N/A, функцията VARPA ще върне различен резултат. Причината е, че VARPA оценява текстовите стойности като нули, докато VARP и VAR.P игнорират текстовите и логическите стойности в препратките. За повече подробности вижте VAR.P срещу VARPA.

Формула за отклонение в Excel - бележки за употреба
За да направите правилно анализ на дисперсията в Excel, следвайте тези прости правила:
- Предоставяйте аргументи като стойности, масиви или препратки към клетки.
- В Excel 2007 и по-нови версии можете да предоставите до 255 аргумента, съответстващи на извадка или популация; в Excel 2003 и по-стари версии - до 30 аргумента.
- Оценяване само на номера в препратките, като се игнорират празните клетки, текстът и логическите стойности, използвайте функцията VAR или VAR.S, за да изчислите дисперсията на извадката, и VARP или VAR.P, за да намерите дисперсията на популацията.
- Да се оцени логически и текст стойности в препратки, използвайте функцията VARA или VARPA.
- Осигурете поне две числови стойности по формулата за дисперсия на извадката и най-малко една числова стойност към формулата за дисперсия на популацията в Excel, в противен случай се появява грешка #DIV/0!.
- Аргументи, съдържащи текст, който не може да бъде интерпретиран като числа, причиняват грешки #VALUE!.
Вариация срещу стандартно отклонение в Excel
Дисперсията несъмнено е полезно понятие в науката, но дава много малко практическа информация. Например, намерихме възрастта на популацията на тигрите в местната зоологическа градина и изчислихме дисперсията, която е равна на 16. Въпросът е - как всъщност можем да използваме това число?
Можете да използвате дисперсията, за да изчислите стандартното отклонение, което е много по-добър показател за размера на вариациите в набора от данни.
Стандартно отклонение се изчислява като корен квадратен от дисперсията. Така че вземаме корен квадратен от 16 и получаваме стандартно отклонение 4.
В комбинация със средната стойност стандартното отклонение може да ви покаже на каква възраст са повечето тигри. Например, ако средната стойност е 8, а стандартното отклонение е 4, повечето тигри в зоопарка са на възраст между 4 години (8 - 4) и 12 години (8 + 4).
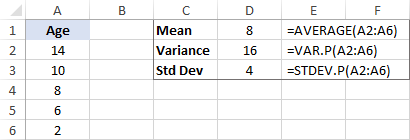
Microsoft Excel разполага със специални функции за изчисляване на стандартното отклонение на извадка и популация. Подробно обяснение на всички функции можете да намерите в това ръководство: Как да изчислим стандартното отклонение в Excel.
Това е начинът да се направи вариация в Excel. За да разгледате по-отблизо формулите, разгледани в този урок, можете да изтеглите нашата примерна работна книга в края на тази публикация. Благодаря ви, че прочетохте, и се надявам да се видим в нашия блог следващата седмица!
Практическа работна тетрадка
Изчисляване на вариация в Excel - примери (.xlsx файл)

