Оглавление
В этом учебном пособии мы рассмотрим, как проводить дисперсионный анализ Excel и какие формулы использовать для нахождения дисперсии выборки и популяции.
Дисперсия - один из самых полезных инструментов в теории вероятностей и статистике. В науке она описывает, насколько далеко каждое число в наборе данных от среднего значения. На практике она часто показывает, насколько сильно что-то меняется. Например, температура вблизи экватора имеет меньшую дисперсию, чем в других климатических зонах. В этой статье мы проанализируем различные методы расчета дисперсии в Excel.
Что такое дисперсия?
Отклонение это мера изменчивости набора данных, которая показывает, насколько сильно разбросаны различные значения. Математически она определяется как среднее квадратичное отклонение от среднего значения.
Чтобы лучше понять, что вы на самом деле вычисляете с помощью дисперсии, пожалуйста, рассмотрите этот простой пример.
Предположим, что в вашем местном зоопарке есть 5 тигров, которым 14, 10, 8, 6 и 2 года.
Чтобы найти дисперсию, выполните следующие простые действия:
- Вычислите среднее значение (простое среднее) пяти чисел:
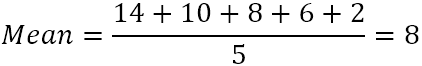
- Из каждого числа вычтите среднее, чтобы найти разницу. Чтобы представить это наглядно, давайте нанесем разницу на график:
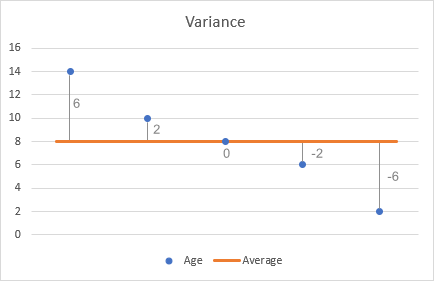
- Возведите в квадрат каждую разницу.
- Вычислите среднее значение разности квадратов.
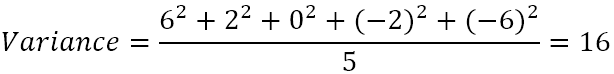
Итак, дисперсия равна 16. Но что на самом деле означает это число?
В действительности дисперсия дает лишь общее представление о дисперсии набора данных. Значение 0 означает отсутствие изменчивости, т.е. все числа в наборе данных одинаковы. Чем больше число, тем больше разброс данных.
Этот пример относится к дисперсии популяции (т.е. 5 тигров - это вся интересующая вас группа). Если ваши данные - это выборка из большей популяции, то вам нужно рассчитать дисперсию выборки, используя немного другую формулу.
Как рассчитать дисперсию в Excel
В Excel существует 6 встроенных функций для расчета дисперсии: VAR, VAR.S, VARP, VAR.P, VARA и VARPA.
Ваш выбор формулы дисперсии определяется следующими факторами:
- Версия Excel, которую вы используете.
- Рассчитываете ли вы выборочную или популяционную дисперсию.
- Нужно ли оценивать или игнорировать текстовые и логические значения.
Функции дисперсии в Excel
В приведенной ниже таблице представлен обзор вариативных функций, доступных в Excel, чтобы помочь вам выбрать формулу, наиболее подходящую для ваших нужд.
| Имя | Версия Excel | Тип данных | Текст и логика |
| VAR | 2000 - 2019 | Образец | Игнорируется |
| VAR.S | 2010 - 2019 | Образец | Игнорируется |
| VARA | 2000 - 2019 | Образец | Оценено |
| VARP | 2000 - 2019 | Население | Игнорируется |
| VAR.P | 2010 - 2019 | Население | Игнорируется |
| VARPA | 2000 - 2019 | Население | Оценено |
VAR.S против VARA и VAR.P против VARPA
VARA и VARPA отличаются от других функций дисперсии только тем, как они обрабатывают логические и текстовые значения в ссылках. В следующей таблице приведена сводка того, как оцениваются текстовые представления чисел и логических значений.
| Тип аргумента | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Логические значения в массивах и ссылках | Игнорируется | Оценено (TRUE=1, FALSE=0) |
| Текстовые представления чисел в массивах и ссылках | Игнорируется | Оценивается как ноль |
| Логические значения и текстовые представления чисел, вводимых непосредственно в аргументы | Оценено (TRUE=1, FALSE=0) | |
| Пустые клетки | Игнорируется | |
Как рассчитать выборочную дисперсию в Excel
A образец это набор данных, взятых из всей совокупности. А дисперсия, рассчитанная по выборке, называется дисперсия выборки .
Например, если вы хотите узнать, как варьируется рост людей, то измерить каждого человека на Земле будет технически невыполнимо. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и оценить рост всего населения на основе этой выборки.
Выборочная дисперсия рассчитывается по этой формуле:
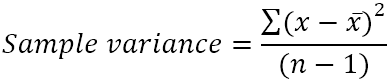
Где:
- x̄ - среднее значение (простое среднее) значений выборки.
- n - размер выборки, т.е. количество значений в выборке.
В Excel существует 3 функции для нахождения выборочной дисперсии: VAR, VAR.S и VARA.
Функция VAR в Excel
Это самая старая функция Excel для оценки дисперсии на основе выборки. Функция VAR доступна во всех версиях Excel с 2000 по 2019 год.
VAR(number1, [number2], ...)Примечание. В Excel 2010 функция VAR была заменена на VAR.S, которая обеспечивает повышенную точность. Хотя функция VAR все еще доступна для обратной совместимости, рекомендуется использовать VAR.S в текущих версиях Excel.
Функция VAR.S в Excel
Это современный аналог функции VAR в Excel. Используйте функцию VAR.S для нахождения выборочной дисперсии в Excel 2010 и более поздних версиях.
VAR.S(number1, [number2], ...)Функция VARA в Excel
Функция Excel VARA возвращает выборочную дисперсию на основе набора чисел, текста и логических значений, как показано в этой таблице.
VARA(значение1, [значение2], ...)Формула выборочной дисперсии в Excel
При работе с числовым набором данных вы можете использовать любую из перечисленных выше функций для расчета выборочной дисперсии в Excel.
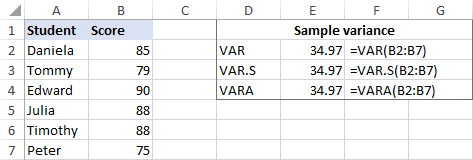
В качестве примера найдем дисперсию выборки, состоящей из 6 предметов (B2:B7). Для этого можно воспользоваться одной из приведенных ниже формул:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Как показано на скриншоте, все формулы возвращают один и тот же результат (округленный до 2 знаков после запятой):
Чтобы проверить результат, выполним расчет var вручную:
- Найдите среднее значение с помощью функции AVERAGE:
= СРЕДНЕЕ(B2:B7)Среднее значение попадает в любую пустую ячейку, скажем, B8.
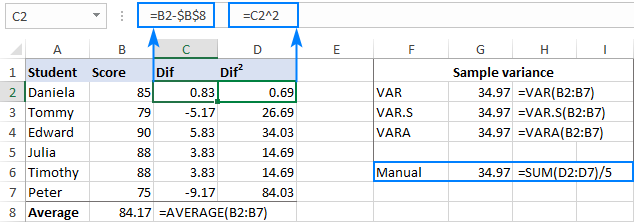
- Вычтите среднее значение из каждого числа в выборке:
=B2-$B$8Различия переходят в колонку C, начиная с C2.
- Возведите в квадрат каждую разность и запишите результаты в столбец D, начиная с D2:
=C2^2 - Сложите квадраты разностей и разделите результат на количество предметов в выборке минус 1:
=SUM(D2:D7)/(6-1)
Как вы можете видеть, результат нашего ручного вычисления var в точности совпадает с числом, возвращаемым встроенными функциями Excel:
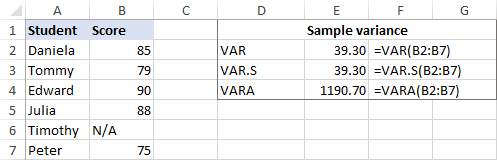
Если ваш набор данных содержит Булево и/или текст Причина в том, что VAR и VAR.S игнорируют любые значения, кроме чисел в ссылках, в то время как VARA оценивает текстовые значения как нули, TRUE как 1, а FALSE как 0. Поэтому, пожалуйста, тщательно выбирайте функцию дисперсии для своих вычислений в зависимости от того, хотите ли вы обрабатывать или игнорировать текстовые и логические значения.
Как рассчитать дисперсию населения в Excel
Население это все члены данной группы, т.е. все наблюдения в изучаемой области. Дисперсия населения описывает, как распределяются точки данных во всей совокупности.
Дисперсию популяции можно найти с помощью этой формулы:
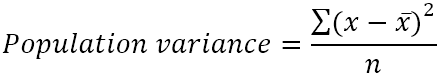
Где:
- x̄ - среднее значение популяции.
- n - размер популяции, т.е. общее количество значений в популяции.
В Excel существует 3 функции для расчета дисперсии популяции: VARP, VAR.P и VARPA.
Функция VARP в Excel
Функция Excel VARP возвращает дисперсию совокупности на основе всего набора чисел. Она доступна во всех версиях Excel с 2000 по 2019 год.
VARP(number1, [number2], ...)Примечание. В Excel 2010 функция VARP была заменена на VAR.P, но она по-прежнему сохраняется для обратной совместимости. Рекомендуется использовать VAR.P в текущих версиях Excel, поскольку нет гарантии, что функция VARP будет доступна в будущих версиях Excel.
Функция VAR.P в Excel
Это улучшенная версия функции VARP, доступная в Excel 2010 и более поздних версиях.
VAR.P(number1, [number2], ...)Функция VARPA в Excel
Функция VARPA вычисляет дисперсию совокупности на основе всего набора чисел, текста и логических значений. Она доступна во всех версиях Excel с 2000 по 2019 год.
VARA(значение1, [значение2], ...)Формула дисперсии популяции в Excel
В примере расчета дисперсии мы нашли дисперсию 5 экзаменационных оценок, предполагая, что эти оценки были выборкой из большей группы студентов. Если вы соберете данные обо всех студентах в группе, эти данные будут представлять всю популяцию, и вы рассчитаете дисперсию популяции, используя вышеуказанные функции.
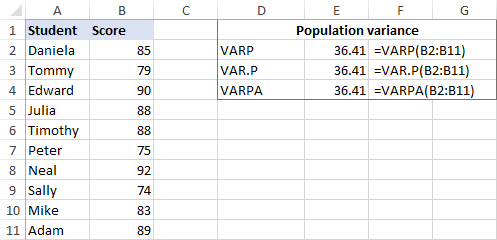
Допустим, у нас есть экзаменационные баллы группы из 10 студентов (B2:B11). Эти баллы составляют всю совокупность, поэтому мы будем проводить дисперсию с помощью этих формул:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
И все формулы будут возвращать одинаковый результат:
Чтобы убедиться, что Excel выполнил дисперсию правильно, вы можете проверить ее с помощью формулы ручного расчета var, показанной на скриншоте ниже:

Если некоторые студенты не сдавали экзамен и вместо номера балла у них стоит N/A, функция VARPA вернет другой результат. Причина в том, что VARPA оценивает текстовые значения как нули, а VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Подробную информацию смотрите в разделе VAR.P против VARPA.

Формула отклонения в Excel - советы по использованию
Чтобы правильно выполнить дисперсионный анализ в Excel, следуйте этим простым правилам:
- Предоставьте аргументы в виде значений, массивов или ссылок на ячейки.
- В Excel 2007 и более поздних версиях вы можете предоставить до 255 аргументов, соответствующих выборке или совокупности; в Excel 2003 и старше - до 30 аргументов.
- Оценивать только номера в ссылках, игнорируя пустые ячейки, текст и логические значения, используйте функцию VAR или VAR.S для расчета дисперсии выборки и VARP или VAR.P для нахождения дисперсии популяции.
- Оценить логический и текст значения в ссылках, используйте функцию VARA или VARPA.
- Обеспечить по меньшей мере два числовых значения формуле выборочной дисперсии и по крайней мере одно числовое значение в формулу дисперсии населения в Excel, иначе возникнет ошибка #DIV/0!
- Аргументы, содержащие текст, который не может быть интерпретирован как число, вызывают ошибку #VALUE!
Дисперсия в сравнении со стандартным отклонением в Excel
Дисперсия, несомненно, полезное понятие в науке, но она дает очень мало практической информации. Например, мы нашли возраст популяции тигров в местном зоопарке и рассчитали дисперсию, которая равна 16. Вопрос в том, как мы можем реально использовать это число?
Вы можете использовать дисперсию для вычисления стандартного отклонения, которое является гораздо более точной мерой количества вариаций в наборе данных.
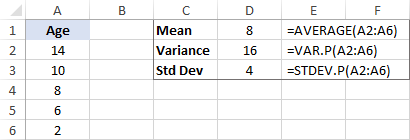
Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Итак, мы берем квадратный корень из 16 и получаем стандартное отклонение 4.
Например, если среднее значение равно 8, а стандартное отклонение равно 4, то большинство тигров в зоопарке имеют возраст от 4 лет (8 - 4) до 12 лет (8 + 4).
В Microsoft Excel есть специальные функции для расчета стандартного отклонения выборки и совокупности. Подробное объяснение всех функций можно найти в этом учебнике: Как рассчитать стандартное отклонение в Excel.
Вот как сделать дисперсию в Excel. Чтобы поближе познакомиться с формулами, рассмотренными в этом учебнике, вы можете скачать наш образец рабочей книги в конце этой заметки. Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая тетрадь
Вычисление дисперсии в Excel - примеры (файл.xlsx)

