如何在Excel中计算方差--样本&；群体方差公式

Michael Brown

26-06-2023 ǞǞǞ
  • Share This
Michael Brown

在本教程中，我们将了解如何对Excel进行方差分析，以及用什么公式来寻找样本和群体的方差。

方差是概率论和统计学中最有用的工具之一。 在科学上，它描述了数据集中的每个数字离平均值有多远。 在实践中，它经常显示某些东西的变化程度。 例如，赤道附近的温度比其他气候区的差异小。 在这篇文章中，我们将分析Excel中计算方差的不同方法。

    什么是差异性？

    差异 在数学上，它被定义为与平均值的平方差的平均值。

    为了更好地理解你实际上在用方差计算什么，请考虑这个简单的例子。

    假设在你当地的动物园里有5只老虎，分别是14岁、10岁、8岁、6岁和2岁。

    要找到差异，请遵循以下简单步骤。

    1. 计算这五个数字的平均值（简单平均数）。

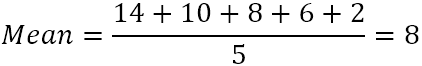
    2. 从每个数字中，减去平均数，就可以找到差异。 为了直观地看到这一点，让我们在图表上绘制差异。

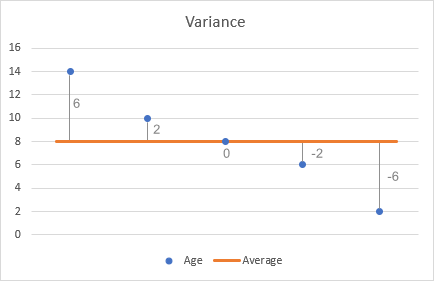
    3. 每一个差值的平方。
    4. 计算出平方差的平均值。

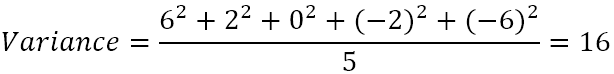
    因此，方差是16。 但这个数字实际上意味着什么呢？

    事实上，方差只是让你对数据集的分散性有一个非常笼统的概念。 数值为0意味着没有变化，也就是说，数据集中的所有数字都是一样的。 数值越大，数据就越分散。

    这个例子是针对群体方差的（即5只老虎是你感兴趣的整个群体）。 如果你的数据是从一个更大的群体中挑选出来的，那么你需要用一个稍微不同的公式来计算样本方差。

    如何在Excel中计算方差

    在Excel中，有6个内置函数可以做方差：VAR、VAR.S、VARP、VAR.P、VARA和VARPA。

    你对方差公式的选择是由以下因素决定的。

    • 你所使用的Excel的版本。
    • 无论你计算的是样本还是群体方差。
    • 你是否要评估或忽略文本和逻辑值。

    Excel方差函数

    下表提供了Excel中可用的变化函数的概述，以帮助你选择最适合你需求的公式。

    命名 Excel版本 数据类型 文本和逻辑
    VAR 2000 - 2019 样品 被忽视的
    VAR.S 2010 - 2019 样品 被忽视的
    VARA 2000 - 2019 样品 已评估
    VARP 2000 - 2019 人口 被忽视的
    VAR.P 2010 - 2019 人口 被忽视的
    VARPA 2000 - 2019 人口 已评估

    VAR.S对VARA，VAR.P对VARPA

    VARA和VARPA与其他变量函数的区别仅在于它们处理引用中的逻辑值和文本值的方式。 下表提供了数字和逻辑值的文本表示的评估方式的摘要。

    论据类型 var, var.s, varp, var.p VARA & VARPA
    数组和引用中的逻辑值 被忽视的 已评估

    (true=1, false=0)

    在数组和引用中的数字的文本表示法 被忽视的 被评估为零
    直接输入参数的逻辑值和数字的文本表示法 已评估

    (true=1, false=0)

    空的细胞 被忽视的

    如何在Excel中计算样本方差

    A 样本 是一组从整个人口中提取的数据。 而从一个样本中计算出来的方差被称为 样本方差 .

    例如，如果你想知道人们的身高是如何变化的，从技术上讲，你要测量地球上的每一个人是不可行的。 解决办法是在人口中抽取一个样本，例如1000人，然后根据这个样本来估计整个人口的身高。

    样本方差是用这个公式计算的。

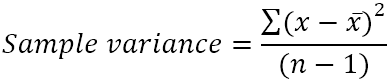
    在哪里？

    • x̄是样本值的平均值（简单平均）。
    • n是样本大小，即样本中的数值数量。

    在Excel中，有3个函数可以找到样本方差：VAR、VAR.S和VARA。

    Excel中的VAR函数

    它是最古老的Excel函数，用于估计基于样本的方差。 VAR函数在Excel 2000至2019年的所有版本中都可用。

    VAR(number1, [number2], ...)

    注意：在Excel 2010中，VAR函数被VAR.S取代，它提供了更好的准确性。 虽然VAR仍然可以向后兼容，但建议在当前版本的Excel中使用VAR.S。

    Excel中的VAR.S函数

    它是Excel VAR函数的现代对应函数。 在Excel 2010及以后的版本中，使用VAR.S函数来查找样本方差。

    VAR.S(number1, [number2], ...)

    Excel中的VARA函数

    Excel VARA函数根据一组数字、文本和逻辑值返回样本方差，如本表所示。

    VARA(value1, [value2], ...)

    Excel中的样本方差公式

    当处理一组数字数据时，你可以使用上述任何一个函数来计算Excel中的样本差异。

    作为一个例子，让我们找出由6个项目组成的样本的方差（B2:B7）。 为此，你可以使用以下公式之一。

    =VAR(B2:B7)

    =VAR.S(B2:B7)

    =VARA(B2:B7)

    如截图所示，所有的公式都返回相同的结果（四舍五入到小数点后2位）。

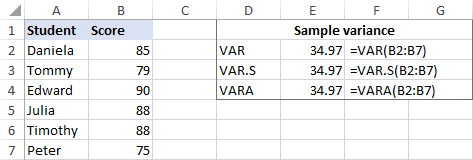
    为了检查结果，让我们手动进行var计算。

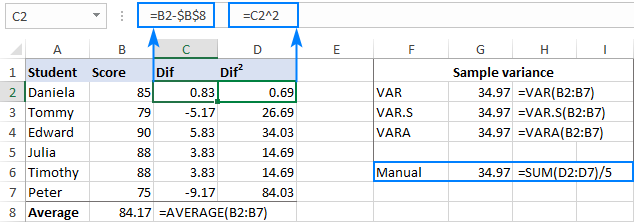
    1. 通过使用AVERAGE函数找到平均值。

      =average(b2:b7)

      平均到任何一个空单元，例如B8。

    2. 从样本中的每个数字中减去平均数。

      =B2-$B$8

      差异进入C列，从C2开始。

    3. 将每个差值平方，并将结果放到D列，从D2开始。

      =C2^2

    4. 将差异的平方相加，然后将结果除以样本中的项目数减去1。

      =sum(d2:d7)/(6-1)

    正如你所看到的，我们手动计算var的结果与Excel的内置函数返回的数字完全相同。

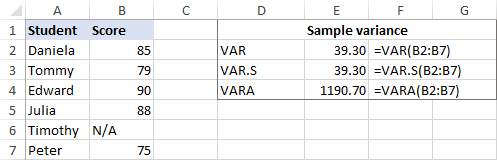
    如果你的数据集包含 布尔型 和/或 文本 原因是VAR和VAR.S忽略了引用中除数字以外的任何值，而VARA将文本值评估为零，TRUE评估为1，FALSE评估为0。 所以，请根据你是否要处理或忽略文本和逻辑，仔细选择计算的变量函数。

    如何在Excel中计算人口差异

    人口 是某一群体的所有成员，即研究领域中的所有观察。 人口变异 描述了整个人口中的数据点是如何分布的。

    群体方差可以通过这个公式找到。

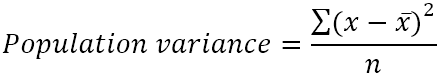
    在哪里？

    • x̄是人口的平均值。
    • n是人口规模，即人口中的数值总数。

    在Excel中，有3个计算人口方差的函数：VARP、VAR.P和VARPA。

    Excel中的VARP函数

    Excel VARP函数返回基于整个数字集的人口方差。 它在Excel 2000至2019年的所有版本中都可用。

    VARP(number1, [number2], ...)

    注意：在Excel 2010中，VARP被VAR.P取代，但为了向后兼容，仍然保留了VAR.P。 建议在当前版本的Excel中使用VAR.P，因为不能保证VARP函数在未来版本的Excel中可用。

    Excel中的VAR.P函数

    它是Excel 2010及以后版本中的VARP函数的改进版。

    VAR.P(number1, [number2], ...)

    Excel中的VARPA函数

    VARPA函数根据整个数字、文本和逻辑值的集合来计算一个群体的方差。 它在Excel 2000到2019的所有版本中都可用。

    VARA(value1, [value2], ...)

    Excel中的人口方差公式

    在var计算的例子中，我们发现5个考试分数的方差，假设这些分数是从一个更大的学生群体中挑选出来的。 如果你收集了这个群体中所有学生的数据，这些数据将代表整个群体，你将通过使用上述函数计算出一个群体方差。

    比方说，我们有一组10名学生（B2:B11）的考试分数。 这些分数构成了整个人口，所以我们将用这些公式做变异。

    =VARP(B2:B11)

    =VAR.P(B2:B11)

    =VARPA(B2:B11)

    而且所有的公式都会返回相同的结果。

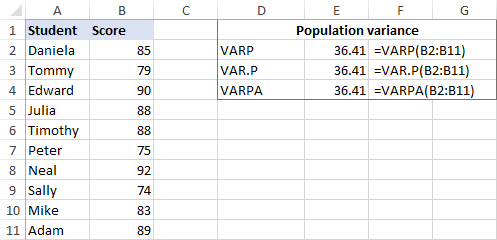
    为了确保Excel已经完成了方差的计算，你可以用下面截图中的手动方差计算公式来检查。

    如果有些学生没有参加考试，并且有N/A而不是分数数字，VARPA函数将返回不同的结果。 原因是VARPA将文本值评估为零，而VARP和VAR.P在引用中忽略了文本和逻辑值。 请参阅VAR.P与VARPA的完整细节。

    Excel中的差异公式--使用说明

    要想在Excel中正确进行差异分析，请遵循以下简单规则。

    • 提供参数为值、数组或单元格引用。
    • 在Excel 2007及以后的版本中，你最多可以提供255个参数，对应于一个样本或群体；在Excel 2003及以前的版本中，最多可以提供30个参数。
    • 只评价 数字 在参考文献中，忽略空单元格、文本和逻辑值，使用VAR或VAR.S函数来计算样本方差，使用VARP或VAR.P来寻找群体方差。
    • 评估 合理 和 文本 的值，使用VARA或VARPA函数。
    • 至少提供 两个数字值 到一个样本方差公式，并且至少有 一个数字值 到Excel中的人口方差公式，否则会出现#DIV/0！的错误。
    • 含有不能被解释为数字的文本的参数会导致#VALUE！错误。

    Excel中的方差与标准差

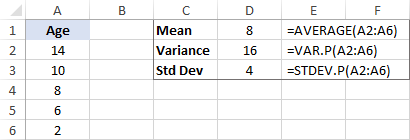
    方差无疑是科学中一个有用的概念，但它提供的实际信息很少。 例如，我们找到了当地动物园里老虎种群的年龄，并计算出方差，等于16。 问题是--我们如何才能真正使用这个数字？

    你可以用方差来计算标准差，这是对数据集变化量的一个更好的衡量。

    标准偏差 因此，我们取16的平方根，得到标准差为4。

    结合平均值，标准差可以告诉你大多数老虎的年龄。 例如，如果平均值是8，标准差是4，那么动物园里的大多数老虎在4岁（8-4）和12岁（8+4）之间。

    Microsoft Excel有专门的函数来计算样本和人群的标准差。 所有函数的详细解释可以在本教程中找到：如何在Excel中计算标准差。

    这就是如何在Excel中进行变量计算的方法。 如果想仔细看看本教程中讨论的公式，欢迎下载本文章末尾的样本工作簿。 感谢你的阅读，希望下周在我们的博客上见到你

    实践工作手册

    在Excel中计算差异 - 示例 (.xlsx文件)

    Previous post 如何删除Excel中的每隔一行或第N行
    Next post 根据列值将谷歌表格中的单元格从多行合并为一行

    Michael Brown is a dedicated technology enthusiast with a passion for simplifying complex processes using software tools. With more than a decade of experience in the tech industry, he has honed his skills in Microsoft Excel and Outlook, as well as Google Sheets and Docs. Michael's blog is dedicated to sharing his knowledge and expertise with others, providing easy-to-follow tips and tutorials for improving productivity and efficiency. Whether you're a seasoned professional or a beginner, Michael's blog offers valuable insights and practical advice for getting the most out of these essential software tools.