Indholdsfortegnelse
I denne vejledning vil vi se på, hvordan man laver variansanalyse i Excel, og hvilke formler man skal bruge til at finde variansen for en prøve og en population.
Varians er et af de mest nyttige værktøjer i sandsynlighedsteori og statistik. I videnskaben beskriver den, hvor langt hvert tal i datasættet er fra gennemsnittet. I praksis viser den ofte, hvor meget noget ændrer sig. F.eks. har temperaturen nær ækvator mindre varians end i andre klimazoner. I denne artikel vil vi analysere forskellige metoder til at beregne varians i Excel.
Hvad er varians?
Afvigelse er et mål for variabiliteten i et datasæt, der angiver, hvor meget forskellige værdier er spredt. Matematisk set defineres det som gennemsnittet af de kvadrerede forskelle fra gennemsnittet.
For bedre at forstå, hvad du rent faktisk beregner med variansen, kan du se på dette enkle eksempel.
Lad os antage, at der er 5 tigre i din lokale zoologiske have, som er 14, 10, 8, 6 og 2 år gamle.
Du kan finde varians ved at følge disse enkle trin:
- Beregn gennemsnittet (det simple gennemsnit) af de fem tal:
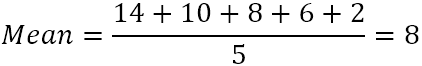
- Fra hvert tal trækkes gennemsnittet for at finde forskellene. For at visualisere dette kan vi plotte forskellene på diagrammet:
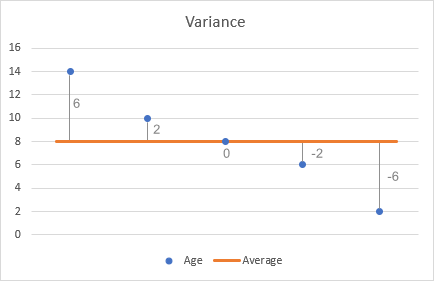
- Kvadrat hver forskel.
- Beregn gennemsnittet af de kvadrerede forskelle.
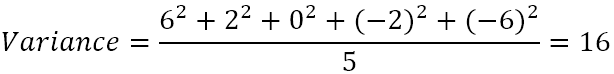
Variansen er altså 16. Men hvad betyder dette tal egentlig?
Variansen giver dig i virkeligheden blot en meget generel idé om spredningen af datasættet. En værdi på 0 betyder, at der ikke er nogen variabilitet, dvs. at alle tallene i datasættet er ens. Jo større tallet er, jo mere spredt er dataene.
Dette eksempel er for populationsvarians (dvs. 5 tigre er hele den gruppe, som du er interesseret i). Hvis dine data er et udvalg fra en større population, skal du beregne stikprøvevariansen ved hjælp af en lidt anden formel.
Hvordan man beregner varians i Excel
Der er 6 indbyggede funktioner til at beregne varians i Excel: VAR, VAR.S, VARP, VAR.P, VARA og VARPA.
Dit valg af variansformel bestemmes af følgende faktorer:
- Den version af Excel, du bruger.
- Om du beregner stikprøve- eller populationsvariansen.
- Om du vil evaluere eller ignorere tekst og logiske værdier.
Excel variansfunktioner
Nedenstående tabel giver en oversigt over de variationsfunktioner, der er tilgængelige i Excel, så du kan vælge den formel, der passer bedst til dine behov.
| Navn | Excel-version | Datatype | Tekst og logik |
| VAR | 2000 - 2019 | Eksempel | Ignoreret |
| VAR.S | 2010 - 2019 | Eksempel | Ignoreret |
| VARA | 2000 - 2019 | Eksempel | Vurderet |
| VARP | 2000 - 2019 | Befolkning | Ignoreret |
| VAR.P | 2010 - 2019 | Befolkning | Ignoreret |
| VARPA | 2000 - 2019 | Befolkning | Vurderet |
VAR.S vs. VARA og VAR.P vs. VARPA
VARA og VARPA adskiller sig kun fra andre variansfunktioner ved den måde, de håndterer logiske værdier og tekstværdier i referencer. Følgende tabel giver et resumé af, hvordan tekstrepræsentationer af tal og logiske værdier evalueres.
| Argument Type | VAR, VAR.S, VARP, VAR.P | VARA & VARPA |
| Logiske værdier i arrays og referencer | Ignoreret | Vurderet (SAND=1, FALSK=0) |
| Tekstrepræsentationer af tal i arrays og referencer | Ignoreret | Vurderet som nul |
| Logiske værdier og tekstrepræsentationer af tal, der indtastes direkte i argumenter | Vurderet (SAND=1, FALSK=0) | |
| Tomme celler | Ignoreret | |
Sådan beregnes stikprøvevarians i Excel
A prøve er et datasæt, der er udtaget fra hele populationen. Og variansen beregnet ud fra en stikprøve kaldes stikprøvevarians .
Hvis man f.eks. ønsker at vide, hvordan folks højde varierer, ville det være teknisk umuligt at måle alle mennesker på jorden. Løsningen er at tage et udsnit af befolkningen, f.eks. 1.000 mennesker, og anslå højden for hele befolkningen på grundlag af dette udsnit.
Prøvevariansen beregnes ved hjælp af denne formel:
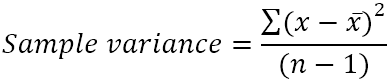
Hvor:
- x̄ er gennemsnittet (det simple gennemsnit) af prøveværdierne.
- n er stikprøvens størrelse, dvs. antallet af værdier i stikprøven.
Der findes 3 funktioner til at finde stikprøvevariansen i Excel: VAR, VAR.S og VARA.
VAR-funktion i Excel
Det er den ældste Excel-funktion til at estimere varians baseret på en stikprøve. VAR-funktionen er tilgængelig i alle versioner af Excel 2000 til 2019.
VAR(nummer1, [nummer2], ...)Bemærk: I Excel 2010 blev VAR-funktionen erstattet af VAR.S, som giver en forbedret nøjagtighed. Selv om VAR stadig er tilgængelig af hensyn til bagudkompatibilitet, anbefales det at bruge VAR.S i de nuværende versioner af Excel.
VAR.S-funktionen i Excel
Det er den moderne pendant til Excel-funktionen VAR. Brug funktionen VAR.S til at finde stikprøvevariansen i Excel 2010 og senere.
VAR.S(nummer1, [nummer2], ...)VARA-funktion i Excel
Excel-funktionen VARA returnerer en prøvevarians baseret på et sæt tal, tekst og logiske værdier som vist i denne tabel.
VARA(value1, [value2], ...)Eksempel på variansformel i Excel
Når du arbejder med et numerisk datasæt, kan du bruge en af ovenstående funktioner til at beregne stikprøvevariansen i Excel.
Lad os f.eks. finde variansen for en stikprøve bestående af 6 emner (B2:B7). Du kan bruge en af nedenstående formler til dette formål:
=VAR(B2:B7)
=VAR.S(B2:B7)
=VARA(B2:B7)
Som vist på skærmbilledet giver alle formlerne det samme resultat (afrundet til 2 decimaler):
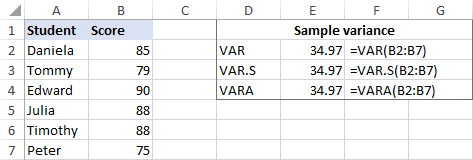
For at kontrollere resultatet skal vi foretage var-beregningen manuelt:
- Find gennemsnittet ved at bruge funktionen AVERAGE:
=GENNEMSNIT(B2:B7)Gennemsnittet går til en tom celle, f.eks. B8.
- Træk gennemsnittet fra hvert tal i prøven:
=B2-$B$8Forskellene går til kolonne C og begynder i C2.
- Kvadratér hver forskel, og sæt resultaterne i kolonne D, begyndende i D2:
=C2^2 - Læg de kvadrerede forskelle sammen og divider resultatet med antallet af emner i prøven minus 1:
=SUM(D2:D7)/(6-1)
Som du kan se, er resultatet af vores manuelle var-beregning nøjagtig det samme som det tal, der returneres af Excels indbyggede funktioner:
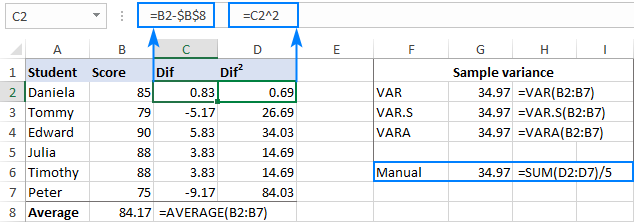
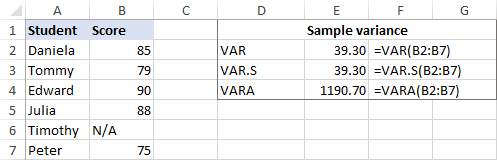
Hvis dit datasæt indeholder Boolean og/eller tekst værdier, vil VARA-funktionen give et andet resultat. Årsagen er, at VAR og VAR.S ignorerer alle andre værdier end tal i referencer, mens VARA evaluerer tekstværdier som nuller, TRUE som 1 og FALSE som 0. Vælg derfor omhyggeligt variansfunktionen til dine beregninger afhængigt af, om du ønsker at behandle eller ignorere tekst og logicals.
Sådan beregnes populationsvarians i Excel
Befolkning er alle medlemmer af en given gruppe, dvs. alle observationer inden for undersøgelsesområdet. Befolkningsvarians beskriver, hvordan datapunkterne i hele populationen er spredt ud.
Befolkningsvariansen kan findes ved hjælp af denne formel:
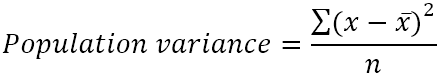
Hvor:
- x̄ er middelværdien af populationen.
- n er populationens størrelse, dvs. det samlede antal værdier i populationen.
Der findes 3 funktioner til at beregne populationsvarians i Excel: VARP, VAR.P og VARPA.
VARP-funktion i Excel
Excel-funktionen VARP returnerer variansen for en population baseret på hele talsættet. Den er tilgængelig i alle versioner af Excel 2000 til 2019.
VARP(nummer1, [nummer2], ...)Bemærk. I Excel 2010 blev VARP erstattet med VAR.P, men er stadig bevaret af hensyn til bagudkompatibilitet. Det anbefales at bruge VAR.P i de nuværende versioner af Excel, da der ikke er nogen garanti for, at VARP-funktionen vil være tilgængelig i fremtidige versioner af Excel.
VAR.P-funktionen i Excel
Det er en forbedret version af VARP-funktionen, der er tilgængelig i Excel 2010 og nyere versioner.
VAR.P(nummer1, [nummer2], ...)VARPA-funktion i Excel
Funktionen VARPA beregner variansen for en population baseret på hele mængden af tal, tekst og logiske værdier. Den er tilgængelig i alle versioner af Excel 2000 til 2019.
VARA(value1, [value2], ...)Formel for befolkningsvarians i Excel
I eksemplet med var-beregning fandt vi en varians for 5 eksamensresultater, idet vi antog, at disse resultater var et udvalg fra en større gruppe af studerende. Hvis du indsamler data om alle studerende i gruppen, vil disse data repræsentere hele populationen, og du vil beregne en populationsvarians ved hjælp af ovenstående funktioner.
Lad os sige, at vi har eksamensresultaterne for en gruppe på 10 elever (B2:B11). Resultaterne udgør hele populationen, så vi vil lave varians med disse formler:
=VARP(B2:B11)
=VAR.P(B2:B11)
=VARPA(B2:B11)
Og alle formlerne vil give det samme resultat:
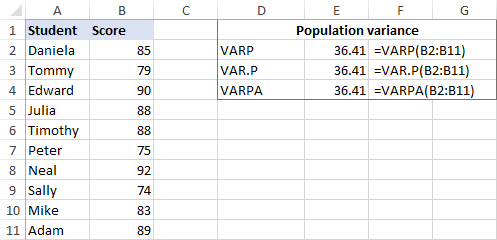
For at sikre dig, at Excel har lavet variansen korrekt, kan du kontrollere den med den manuelle var-beregningsformel, der er vist i skærmbilledet nedenfor:

Hvis nogle af eleverne ikke tog eksamen og har N/A i stedet for et pointtal, vil VARPA-funktionen give et andet resultat. Årsagen er, at VARPA evaluerer tekstværdier som nuller, mens VARP og VAR.P ignorerer tekst- og logiske værdier i referencer. Se VAR.P vs. VARPA for at få yderligere oplysninger.

Variansformel i Excel - brugsanvisninger
Hvis du vil lave variansanalyse i Excel korrekt, skal du følge disse enkle regler:
- Angiv argumenter som værdier, arrays eller cellereferencer.
- I Excel 2007 og senere kan du angive op til 255 argumenter, der svarer til en stikprøve eller population; i Excel 2003 og tidligere - op til 30 argumenter.
- For kun at evaluere numre i referencer, idet der ses bort fra tomme celler, tekst og logiske værdier, skal du bruge funktionen VAR eller VAR.S til at beregne stikprøvevariansen og VARP eller VAR.P til at finde populationsvariansen.
- At evaluere logisk og tekst værdier i referencer, skal du bruge VARA- eller VARPA-funktionen.
- Der skal mindst to numeriske værdier til en prøvevariansformel og mindst en numerisk værdi til en formel for populationsvarians i Excel, ellers opstår der en #DIV/0! fejl.
- Argumenter, der indeholder tekst, som ikke kan fortolkes som tal, forårsager #VALUE! fejl.
Varians vs. standardafvigelse i Excel
Varians er uden tvivl et nyttigt begreb i videnskaben, men det giver meget lidt praktisk information. Vi har f.eks. fundet alderen på tigerpopulationen i en lokal zoologisk have og beregnet variansen, som er lig med 16. Spørgsmålet er, hvordan vi rent faktisk kan bruge dette tal.
Du kan bruge varians til at beregne standardafvigelsen, som er et langt bedre mål for mængden af variation i et datasæt.
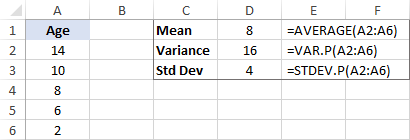
Standardafvigelse beregnes som kvadratroden af variansen, så vi tager kvadratroden af 16 og får en standardafvigelse på 4.
Sammen med gennemsnittet kan standardafvigelsen fortælle dig, hvor gamle de fleste tigre er. Hvis gennemsnittet f.eks. er 8 og standardafvigelsen 4, er de fleste tigre i zoologisk have mellem 4 år (8 - 4) og 12 år (8 + 4).
Microsoft Excel har særlige funktioner til at beregne standardafvigelsen for en stikprøve og en population. Du kan finde en detaljeret forklaring på alle funktionerne i denne vejledning: Sådan beregner du standardafvigelse i Excel.
Sådan gør du varians i Excel. Hvis du vil se nærmere på de formler, der er beskrevet i denne vejledning, er du velkommen til at downloade vores prøvearbejdsmappe i slutningen af dette indlæg. Tak fordi du læste med og håber at se dig på vores blog i næste uge!
Arbejdsbog til øvelser
Beregne varians i Excel - eksempler (.xlsx-fil)

