Table of contents
本教程展示了如何在Excel中使用XIRR来计算时间不规则的现金流的内部收益率(IRR),以及如何制作自己的XIRR计算器。
当你面临一个资本密集型的决策时,计算内部收益率是可取的,因为它可以让你比较不同投资的预计收益,为决策提供一个量化的基础。
在之前的教程中,我们看了如何用Excel的IRR函数来计算内部收益率。 这种方法快速而直接,但它有一个基本的限制--IRR函数假设所有的现金流都在相等的时间间隔内发生,比如每月或每年。 然而,在现实生活中,现金流入和流出往往发生在不规则的间隔内。值得庆幸的是,在这种情况下,Microsoft Excel有另一个函数来寻找内部收益率,本教程将教你如何使用它。
Excel中的XIRR函数
Excel的XIRR函数返回一系列现金流的内部收益率,这些现金流可能是周期性的,也可能不是。
该功能是在Excel 2007中引入的,并在Excel 2010、Excel 2013、Excel 2016、Excel 2019和Excel for Office 365的所有后期版本中可用。
XIRR函数的语法如下。
XIRR(value, dates, [guess])在哪里?
- 价值观 (要求) - 一个数组或一个单元格范围,代表一系列的流入和流出。
- 日期 (必填) - 与现金流相对应的日期。 日期可以按任何顺序出现,但初始投资的日期必须在数组中的第一位。
- 猜测 (可选) - 以百分比或小数形式提供的预期内部收益率。 如果省略,Excel使用默认的0.1(10%)比率。
例如,要计算A2:A5中的一系列现金流和B2:B5中的日期的内部收益率,你会使用这个公式。
=xirr(a2:a5, b2:b5)
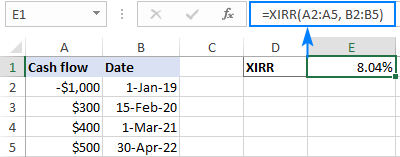
提示:为了使结果正确显示,请确保 百分比 格式是为公式单元格设置的。
关于XIRR功能,你应该知道的6件事
下面的说明将帮助你更好地理解XIRR函数的内部机制,并在你的工作表中最有效地使用它。
- Excel中的XIRR是为计算时间不等的现金流的内部收益率而设计的。 对于确切支付日期未知的定期现金流,你可以使用IRR函数。
- 数值范围必须至少包含一个正值(收入)和一个负值(流出的款项)。
- 如果第一个值是一个支出(初始投资),它必须用一个负数来表示。 初始投资没有被贴现;随后的付款被带回第一个现金流的日期,并根据一年365天进行贴现。
- 所有的日期都被截断为整数,这意味着日期中代表时间的小数部分被去除。
- 日期必须是有效的Excel日期,作为对包含日期的单元格的引用或公式的结果输入,如DATE函数。 如果日期以文本格式输入,可能会出现问题。
- Excel中的XIRR总是返回一个 年化内部收益率 甚至在计算每月或每周的现金流时也是如此。
在Excel中计算XIRR
Excel中的XIRR函数使用试错的方法来寻找满足这一方程式的比率。

在哪里?
- P--现金流(支付)
- d - 日期
- i - 周期号
- n - 阶段总数
如果提供了猜测,则从猜测开始,如果没有,则从默认的10%开始,Excel通过迭代来达到0.000001%的准确率。 如果经过100次尝试还没有找到准确率,则返回#NUM!错误。
为了检查这个公式的有效性,让我们用XIRR公式的结果来测试它。 为了简化我们的计算,我们将使用以下数组公式(请记住,任何数组公式必须通过按Ctrl + Shift + Enter来完成)。
=SUM(A2:A5/((1+$E$1)^((B2:B5-$B$2)/365)))
在哪里?
- A2:A5是现金流
- B2:B5为日期
- E1是XIRR所返回的比率
如下面的截图所示,结果非常接近于零。 Q.E.D.:)
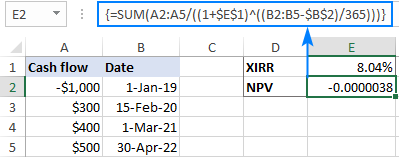
如何在Excel中计算XIRR--公式示例
下面是几个例子,展示了Excel中XIRR函数的常见用途。
Excel中的基本XIRR公式
假设你在2017年投资了1,000美元,并期望在未来6年内获得一些利润。 要找到这项投资的内部回报率,请使用这个公式。
=xirr(a2:a8, b2:b8)
其中A2:A8为现金流,B2:B8为现金流对应的日期。
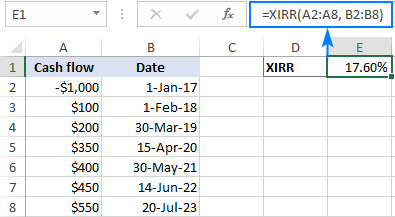
为了判断这项投资的盈利能力,将XIRR的输出与你公司的 加权平均资本成本 或 障碍率 如果回报率高于资本成本,该项目可以被认为是一项好的投资。
在比较几种投资方案时,请记住,预测的回报率只是你在做决定前应该估计的因素之一。 更多信息,请参见什么是内部回报率(IRR)?
Excel XIRR函数的完整形式
如果你知道你从这个或那个投资中期待什么样的回报,你可以把你的期待作为一个猜测。 当一个明显正确的XIRR公式抛出一个#NUM!错误时,它尤其有帮助。
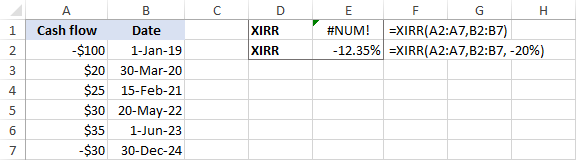
对于下面的数据输入,没有猜测的XIRR公式会返回一个错误。
=xirr(a2:a7, b2:b7)
的预期回报率(-20%),把 猜测 参数帮助Excel得出结果。
=xirr(a2:a7, b2:b7, -20%)
如何计算每月现金流的XIRR
对于初学者,请记住这一点--无论你计算的是什么现金流,Excel的XIRR函数都会产生一个 年收益率 .
为了确定这一点,让我们找出每月和每年发生的同一系列现金流(A2:A8)的IRR(日期在B2:B8)。
=xirr(a2:a8, b2:b8)
正如你在下面的截图中所看到的,内部收益率从年度现金流的7.68%上升到月度现金流的约145%!这个差异似乎太高了,仅凭货币的时间价值因素是无法证明的。
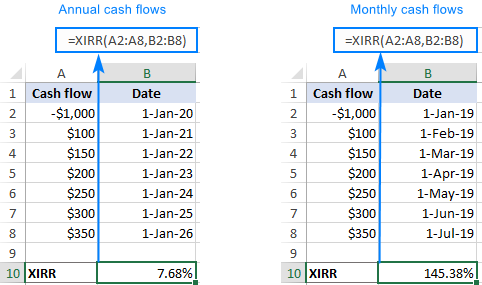
为了找到一个近似的 每月的XIRR ,你可以使用下面的计算,其中E1是常规XIRR公式的结果。
=(1+E1)^(1/12)-1
或者你可以将XIRR直接嵌入到方程式中。
=(1+XIRR(A2:A8,B2:B8))^(1/12)-1
作为额外的检查,让我们对相同的现金流使用IRR函数。 请记住,IRR也会计算出一个近似的比率,因为它假设所有的时间段都是相等的。
=IRR(A2:A8)
作为这些计算的结果,我们得到的每月XIRR为7.77%,这与IRR公式得出的7.68%非常接近。
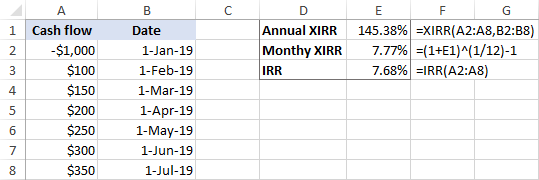
结论 如果你想得到月度现金流的年化内部收益率,请使用XIRR函数的纯粹形式;要得到月度内部收益率,请应用上述的调整。
Excel XIRR模板
为了快速获得不同项目的内部收益率,你可以为Excel创建一个多功能的XIRR计算器。 下面是方法。
- 在两个单独的栏目(本例中的A和B)中输入现金流和日期。
- 创建两个动态定义的范围,命名为 现金流 和 日期 技术上讲,这将是命名的公式。
现金流。
=OFFSET(Sheet1! $A$2,0,0,COUNT(Sheet1! $A:$A),1)日期。
=OFFSET(Sheet1! $B$2,0,0,COUNT(Sheet1! $B:$B),1)在哪里? 第1张 是你工作表的名称,A2是第一个现金流,B2是第一个日期。
详细的步骤说明,请看如何在Excel中创建一个动态命名的范围。
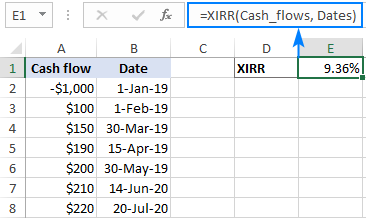
- 为XIRR公式提供你所创建的动态定义名称。
=XIRR(Cash_flows, Dates)
完成了!你现在可以随心所欲地添加或删除现金流,而你的动态XIRR公式将相应地重新计算。
Excel中的XIRR与IRR
Excel的XIRR和IRR函数的主要区别在于此。
- 内部收益率 假设一系列现金流中的所有时期都是相等的。 你用这个函数来寻找定期现金流的内部收益率,如每月、每季度或每年。
- XIRR 允许你为每个单独的现金流指定一个日期。 因此,使用这个函数来计算不一定是定期的现金流的IRR。
一般来说,如果你知道确切的付款日期,建议使用XIRR,因为它能提供更好的计算准确性。
作为一个例子,让我们比较一下相同现金流的IRR和XIRR的结果。
如果所有的付款都发生在 定期的间隔 ,这些函数返回的结果非常接近。
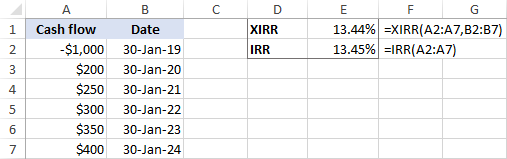
如果现金流的时间是 不平等 ,结果之间的差异是相当大的。
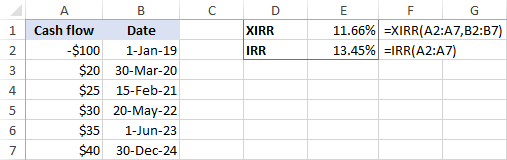
Excel中的XIRR和XNPV
XIRR与XNPV函数密切相关,因为XIRR的结果是导致净现值为零的贴现率。 换句话说,XIRR就是XNPV=0。 下面的例子展示了Excel中XIRR和XNPV的关系。
假设你正在考虑一些投资机会,并想考察这项投资的净现值和内部收益率。
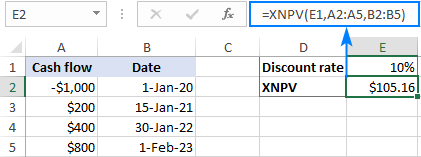
在A2:A5中的现金流,B2:B5中的日期和E1中的贴现率,下面的XNPV公式会给你未来现金流的净现值。
=xnpv(e1, a2:a5, b2:b5)
正的净现值表明该项目是有利可图的。
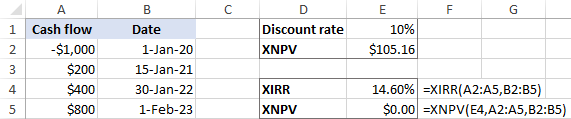
现在,让我们找出使净现值为零的贴现率。 为此,我们使用XIRR函数。
=xirr(a2:a5, b2:b5)
为了检查XIRR产生的比率是否真的导致净现值为零,把它放在 率 你的XNPV公式的参数。
=xnpv(e4, a2:a5, b2:b5)
或者嵌入整个XIRR函数。
=xnpv(xirr(a2:a5, b2:b5), a2:a5, b2:b5)
是的,四舍五入到小数点后2位的XNPV确实等于零。
要显示准确的净现值,可以选择显示更多的小数位,或者对XNPV单元格应用科学格式。 这将产生与此类似的结果。
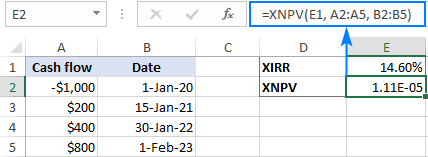
如果你不熟悉科学记数法,请进行以下计算,将其转换为小数。
1.11E-05 = 1.11*10^-5 = 0.0000111
Excel的XIRR函数不工作
如果你在Excel中遇到了XNPV函数的问题,下面是需要检查的要点。
#NUM!错误
由于以下原因,可能会出现#NUM错误。
- ǞǞǞ 价值 和 枣庄 范围有不同的长度(不同的列数或行数)。
- ǞǞǞ 价值 数组不包含至少一个正值和一个负值。
- 随后的任何一个日期都比第一个日期早。
- 迭代100次后仍未找到结果。 在这种情况下,尝试不同的猜测。
#VALUE!错误
一个#VALUE错误可能是由以下原因造成的。
- 提供的任何 价值 为非数字型。
- 一些提供的日期不能被确定为有效的Excel日期。
这就是在Excel中计算XIRR的方法。 如果想仔细看看本教程中讨论的公式,欢迎下载我们下面的样本工作簿。 感谢你的阅读,希望下周在我们的博客上见到你!
供下载的实践工作手册
XIRR Excel模板(.xlsx文件)。

