Mục lục
Hướng dẫn chỉ ra cách sử dụng XIRR trong Excel để tính tỷ lệ hoàn vốn nội bộ (IRR) cho các dòng tiền có thời gian không đều và cách tạo máy tính XIRR của riêng bạn.
Khi nào bạn đang phải đối mặt với một quyết định sử dụng nhiều vốn, việc tính toán tỷ lệ hoàn vốn nội bộ là điều nên làm vì nó cho phép bạn so sánh lợi nhuận dự kiến cho các khoản đầu tư khác nhau và đưa ra cơ sở định lượng để đưa ra quyết định.
Trong hướng dẫn trước của chúng tôi, chúng tôi đã xem xét cách tính tỷ lệ hoàn vốn nội bộ bằng hàm IRR của Excel. Phương pháp đó nhanh chóng và đơn giản, nhưng nó có một hạn chế cơ bản – hàm IRR giả định rằng tất cả các dòng tiền xảy ra ở các khoảng thời gian bằng nhau, chẳng hạn như hàng tháng hoặc hàng năm. Tuy nhiên, trong các tình huống thực tế, dòng tiền vào và ra thường xảy ra không đều đặn. Rất may, Microsoft Excel có một chức năng khác để tìm IRR trong những trường hợp như vậy và hướng dẫn này sẽ hướng dẫn bạn cách sử dụng nó.
Hàm XIRR trong Excel
XIRR của Excel hàm trả về tỷ lệ hoàn vốn nội bộ cho một loạt các dòng tiền có thể có hoặc không có tính định kỳ.
Hàm này được giới thiệu trong Excel 2007 và có sẵn trong tất cả các phiên bản mới hơn của Excel 2010, Excel 2013, Excel 2016 , Excel 2019 và Excel cho Office 365.
Cú pháp của hàm XIRR như sau:
XIRR(giá trị, ngày, [đoán])Ở đâu:
- Giá trị (bắt buộc) – mộtmảng hoặc một dải ô đại diện cho một loạt dòng tiền vào và dòng tiền ra.
- Ngày (bắt buộc) – ngày tương ứng với dòng tiền. Các ngày có thể xuất hiện theo bất kỳ thứ tự nào, nhưng ngày của khoản đầu tư ban đầu phải ở vị trí đầu tiên trong mảng.
- Đoán (tùy chọn) – IRR dự kiến được cung cấp dưới dạng phần trăm hoặc số thập phân. Nếu bỏ qua, Excel sẽ sử dụng tỷ lệ mặc định là 0,1 (10%).
Ví dụ: để tính IRR cho chuỗi dòng tiền trong A2:A5 và ngày trong B2:B5, bạn sẽ sử dụng công thức này:
=XIRR(A2:A5, B2:B5)
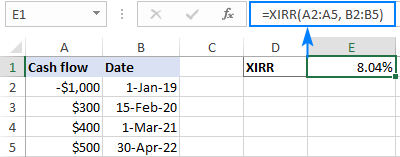
Mẹo. Để kết quả hiển thị chính xác, vui lòng đảm bảo rằng định dạng Phần trăm được đặt cho ô công thức.
6 điều bạn nên biết về hàm XIRR
Những lưu ý sau đây sẽ giúp bạn hiểu rõ hơn về cơ chế bên trong của hàm XIRR và sử dụng hàm này trong trang tính của bạn một cách hiệu quả nhất.
- XIRR trong Excel được thiết kế để tính tỷ lệ hoàn vốn nội bộ cho các dòng tiền với thời gian không đồng đều. Đối với các dòng tiền định kỳ không xác định ngày thanh toán chính xác, bạn có thể sử dụng hàm IRR.
- Phạm vi giá trị phải chứa ít nhất một giá trị dương (thu nhập) và một giá trị âm (thanh toán đi).
- Nếu giá trị đầu tiên là chi phí (đầu tư ban đầu), giá trị này phải được biểu thị bằng số âm. Khoản đầu tư ban đầu không được chiết khấu; các khoản thanh toán tiếp theo được đưa trở lại ngày của dòng tiền đầu tiên và dựa trên chiết khấutrên một năm có 365 ngày.
- Tất cả các ngày được cắt bớt thành số nguyên, nghĩa là phần phân số của ngày đại diện cho thời gian bị loại bỏ.
- Ngày phải là ngày Excel hợp lệ được nhập dưới dạng tham chiếu đến các ô chứa ngày tháng hoặc kết quả của công thức chẳng hạn như hàm DATE. Nếu ngày được nhập ở định dạng văn bản thì có thể xảy ra sự cố.
- XIRR trong Excel luôn trả về IRR hàng năm ngay cả khi tính toán dòng tiền hàng tháng hoặc hàng tuần.
Tính toán XIRR trong Excel
Hàm XIRR trong Excel sử dụng phương pháp thử và sai để tìm tỷ lệ thỏa mãn phương trình này:

Ở đâu:
- P - dòng tiền (thanh toán)
- d - ngày
- i - số kỳ
- n - tổng số kỳ
Bắt đầu với dự đoán nếu được cung cấp hoặc với 10% mặc định nếu không, Excel sẽ lặp lại để đi đến kết quả với độ chính xác 0,000001%. Nếu sau 100 lần thử không tìm thấy tỷ lệ chính xác, lỗi #NUM! lỗi được trả về.
Để kiểm tra tính hợp lệ của phương trình này, hãy kiểm tra nó dựa trên kết quả của công thức XIRR. Để đơn giản hóa phép tính của chúng tôi, chúng tôi sẽ sử dụng công thức mảng sau (hãy nhớ rằng bất kỳ công thức mảng nào cũng phải được hoàn thành bằng cách nhấn Ctrl + Shift + Enter ):
=SUM(A2:A5/((1+$E$1)^((B2:B5-$B$2)/365)))
Ở đâu:
- A2:A5 là dòng tiền
- B2:B5 là ngày tháng
- E1 là tỷ suất trả về của XIRR
Như thể hiện trong ảnh chụp màn hình bên dưới, kết quả rất gầnvề không. Q.E.D. :)
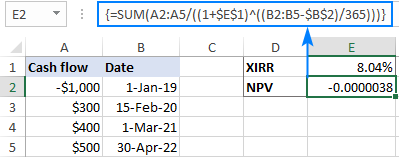
Cách tính XIRR trong Excel – ví dụ về công thức
Dưới đây là một vài ví dụ minh họa các cách sử dụng phổ biến của hàm XIRR trong Excel.
Công thức XIRR cơ bản trong Excel
Giả sử bạn đã đầu tư 1.000 USD vào năm 2017 và mong muốn nhận được một số lợi nhuận trong 6 năm tới. Để tìm tỷ lệ hoàn vốn nội bộ cho khoản đầu tư này, hãy sử dụng công thức sau:
=XIRR(A2:A8, B2:B8)
Trong đó A2:A8 là dòng tiền và B2:B8 là ngày tương ứng với dòng tiền:
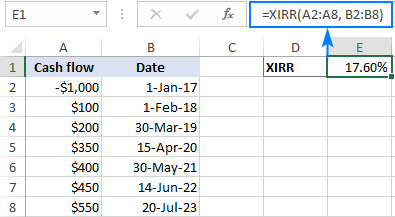
Để đánh giá khả năng sinh lời của khoản đầu tư này, hãy so sánh kết quả XIRR với chi phí vốn bình quân gia quyền hoặc tỷ lệ vượt rào của công ty bạn. Nếu tỷ suất hoàn vốn cao hơn chi phí vốn thì dự án có thể được coi là một khoản đầu tư tốt.
Khi so sánh một số phương án đầu tư, hãy nhớ rằng tỷ suất hoàn vốn dự kiến chỉ là một trong những yếu tố mà bạn nên ước tính trước khi đưa ra quyết định. Để biết thêm thông tin, vui lòng xem Tỷ lệ hoàn vốn nội bộ (IRR) là gì?
Mẫu hoàn chỉnh của hàm XIRR trong Excel
Trong trường hợp bạn biết mình mong đợi loại tiền lãi nào từ cái này hoặc cái kia đầu tư, bạn có thể sử dụng kỳ vọng của mình để phỏng đoán. Nó đặc biệt hữu ích khi một công thức XIRR rõ ràng chính xác đưa ra lỗi #NUM! lỗi.
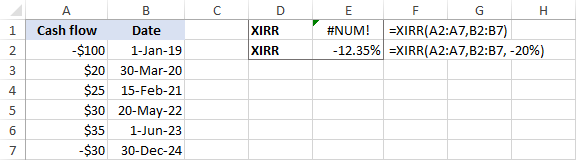
Đối với dữ liệu đầu vào được hiển thị bên dưới, công thức XIRR không có dự đoán sẽ trả về lỗi:
=XIRR(A2:A7, B2:B7)
Tỷ lệ hoàn vốn dự đoán(-20%) đưa vào đối số guess giúp Excel đi đến kết quả:
=XIRR(A2:A7, B2:B7, -20%)
Cách tính XIRR cho dòng tiền hàng tháng
Đối với người mới bắt đầu, hãy nhớ điều này – bất kể dòng tiền nào bạn đang tính toán, hàm XIRR của Excel sẽ tạo ra tỷ lệ hoàn vốn hàng năm .
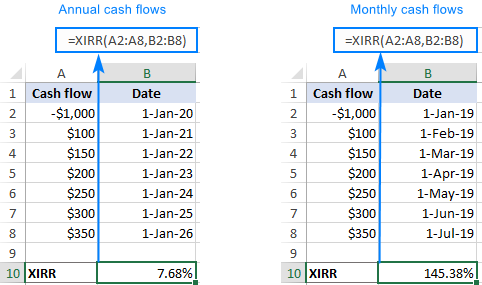
Để đảm bảo này, hãy tìm IRR cho cùng một chuỗi dòng tiền (A2:A8) xảy ra hàng tháng và hàng năm (ngày nằm trong B2:B8):
=XIRR(A2:A8, B2:B8)
Như bạn có thể thấy trong ảnh chụp màn hình bên dưới, IRR tăng từ 7,68% trong trường hợp dòng tiền hàng năm lên khoảng 145% đối với dòng tiền hàng tháng! Sự khác biệt dường như quá cao để có thể chứng minh chỉ bằng giá trị thời gian của yếu tố tiền tệ:
Để tìm XIRR hàng tháng gần đúng, bạn có thể sử dụng thông tin bên dưới phép tính, trong đó E1 là kết quả của công thức XIRR thông thường:
=(1+E1)^(1/12)-1
Hoặc bạn có thể nhúng trực tiếp XIRR vào phương trình:
=(1+XIRR(A2:A8,B2:B8))^(1/12)-1
As kiểm tra bổ sung, hãy sử dụng chức năng IRR trên cùng một dòng tiền. Xin lưu ý rằng IRR cũng sẽ tính tỷ lệ gần đúng vì nó giả định rằng tất cả các khoảng thời gian đều bằng nhau:
=IRR(A2:A8)
Kết quả của những tính toán này, chúng tôi nhận được XIRR hàng tháng là 7,77 %, rất gần với 7,68% được tạo ra bởi công thức IRR:
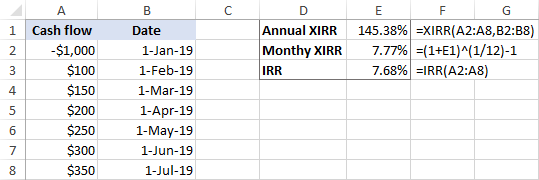
Kết luận : nếu bạn đang tìm kiếm IRR hàng năm cho tiền mặt hàng tháng dòng chảy, hãy sử dụng hàm XIRR ở dạng thuần túy; để nhận được IRR hàng tháng, hãy đăng kýđiều chỉnh được mô tả ở trên.
Mẫu XIRR Excel
Để nhanh chóng nhận được tỷ lệ hoàn vốn nội bộ cho các dự án khác nhau, bạn có thể tạo một máy tính XIRR linh hoạt cho Excel. Dưới đây là cách thực hiện:
- Nhập dòng tiền và ngày vào hai cột riêng lẻ (A và B trong ví dụ này).
- Tạo hai phạm vi được xác định động, có tên là Dòng_tiền và Ngày . Về mặt kỹ thuật, đó sẽ được đặt tên theo công thức:
Cash_flows:
=OFFSET(Sheet1!$A$2,0,0,COUNT(Sheet1!$A:$A),1)Dates:
=OFFSET(Sheet1!$B$2,0,0,COUNT(Sheet1!$B:$B),1)Where Sheet1 is tên bảng tính của bạn, A2 là dòng tiền đầu tiên và B2 là ngày đầu tiên.
Để biết hướng dẫn chi tiết từng bước, vui lòng xem Cách tạo phạm vi động được đặt tên trong Excel.
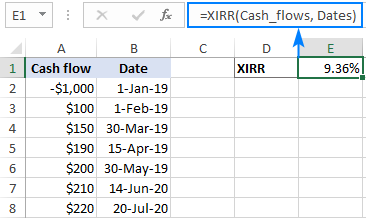
- Cung cấp các tên được xác định động mà bạn đã tạo cho công thức XIRR:
=XIRR(Cash_flows, Dates)
Hoàn tất! Giờ đây, bạn có thể thêm hoặc xóa bao nhiêu dòng tiền tùy thích và công thức XIRR động của bạn sẽ tính toán lại cho phù hợp:
XIRR so với IRR trong Excel
Sự khác biệt chính giữa các hàm XIRR và IRR của Excel là:
- IRR giả định rằng tất cả các giai đoạn trong một chuỗi các dòng tiền đều bằng nhau. Bạn sử dụng chức năng này để tìm tỷ lệ hoàn vốn nội bộ cho các dòng tiền định kỳ, chẳng hạn như hàng tháng, hàng quý hoặc hàng năm.
- XIRR cho phép bạn chỉ định ngày cho từng dòng tiền riêng lẻ. Vì vậy, hãy sử dụng hàm này để tính IRR cho các dòng tiền không nhất thiết phải theo định kỳ.
Nói chung,nếu bạn biết chính xác ngày thanh toán, bạn nên sử dụng XIRR vì nó mang lại độ chính xác tính toán cao hơn.
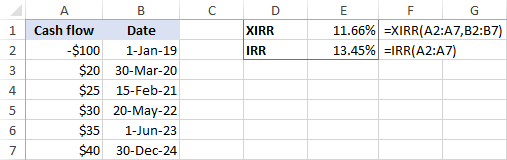
Ví dụ: hãy so sánh kết quả của IRR và XIRR cho cùng một dòng tiền:
Nếu tất cả các khoản thanh toán xảy ra ở khoảng thời gian đều đặn , thì các hàm trả về kết quả rất gần:
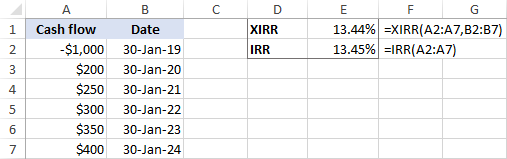
Nếu thời gian của dòng tiền là không bằng nhau , thì sự khác biệt giữa các kết quả là khá lớn:
XIRR và XNPV trong Excel
XIRR có liên quan chặt chẽ với hàm XNPV vì kết quả của XIRR là tỷ lệ chiết khấu dẫn đến giá trị hiện tại ròng bằng không. Nói cách khác, XIRR là XNPV = 0. Ví dụ sau minh họa mối quan hệ giữa XIRR và XNPV trong Excel.
Giả sử bạn đang xem xét một số cơ hội đầu tư và muốn kiểm tra cả giá trị hiện tại ròng và tỷ lệ nội bộ lợi tức của khoản đầu tư này.
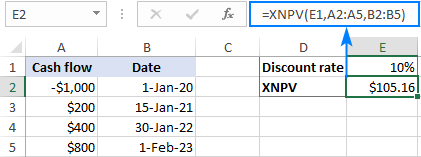
Với dòng tiền trong A2:A5, ngày trong B2:B5 và tỷ lệ chiết khấu trong E1, công thức XNPV sau đây sẽ cho bạn giá trị hiện tại ròng của dòng tiền trong tương lai:
=XNPV(E1, A2:A5, B2:B5)
NPV dương cho thấy dự án có lãi:
Bây giờ, hãy tìm tỷ lệ chiết khấu sẽ tạo ra giá trị hiện tại ròng số không. Đối với điều này, chúng tôi sử dụng hàm XIRR:
=XIRR(A2:A5, B2:B5)
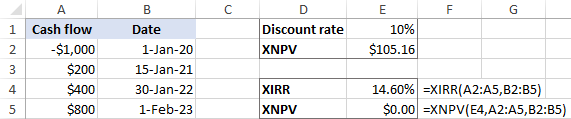
Để kiểm tra xem tỷ lệ do XIRR tạo ra có thực sự dẫn đến NPV bằng 0 hay không, hãy đặt nó vào đối số rate của XNPV của bạncông thức:
=XNPV(E4, A2:A5, B2:B5)
Hoặc nhúng toàn bộ hàm XIRR:
=XNPV(XIRR(A2:A5, B2:B5), A2:A5, B2:B5)
Đúng vậy, XNPV được làm tròn đến 2 chữ số thập phân bằng 0:
Để hiển thị giá trị NPV chính xác, hãy chọn hiển thị nhiều chữ số thập phân hơn hoặc áp dụng định dạng Khoa học cho ô XNPV. Điều đó sẽ tạo ra kết quả tương tự như sau:
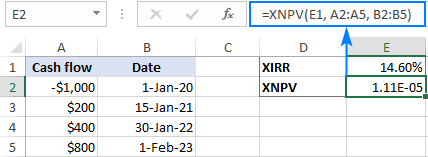
Nếu bạn không quen với ký hiệu khoa học, hãy thực hiện phép tính sau để chuyển đổi nó thành số thập phân:
1.11E-05 = 1.11*10^-5 = 0.0000111
Hàm XIRR của Excel không hoạt động
Nếu bạn gặp sự cố với hàm XNPV trong Excel, dưới đây là những điểm chính cần kiểm tra.
#NUM ! lỗi
Lỗi #NUM có thể xảy ra vì những lý do sau:
- Các phạm vi giá trị và ngày có độ dài khác nhau (khác nhau số lượng cột hoặc hàng).
- Mảng giá trị không chứa ít nhất một giá trị dương và một giá trị âm.
- Bất kỳ ngày nào tiếp theo đều sớm hơn ngày đầu tiên date.
- Không tìm thấy kết quả sau 100 lần lặp lại. Trong trường hợp này, hãy thử đoán khác.
#VALUE! lỗi
Lỗi #VALUE có thể do nguyên nhân sau:
- Bất kỳ giá trị nào được cung cấp đều không phải là số.
- Một số trong số các ngày đã cung cấp không thể được xác định là ngày Excel hợp lệ.
Đó là cách bạn tính toán XIRR trong Excel. Để xem kỹ hơn các công thức được thảo luận trong hướng dẫn này, bạn có thể tải xuống mẫu của chúng tôisổ làm việc dưới đây. Tôi cảm ơn bạn đã đọc và hy vọng sẽ gặp bạn trên blog của chúng tôi vào tuần tới!
Sách bài tập thực hành để tải xuống
Mẫu XIRR Excel (tệp .xlsx)

