Opplæringen viser hvordan du gjør kvadratrot i Excel, samt hvordan du beregner N-te rot av en hvilken som helst verdi.

Å kvadrere et tall og ta en kvadratrot er svært vanlige operasjoner i matematikk. Men hvordan gjør du kvadratrot i Excel? Enten ved å bruke SQRT-funksjonen eller ved å heve et tall til potensen 1/2. Følgende eksempler viser alle detaljer.

Hvordan kvadratrot i Excel ved hjelp av SQRT-funksjonen

Den enkleste måten å gjøre kvadratrot i Excel er ved å bruke funksjonen spesialdesignet for dette:

Hvor tall er tallet eller referansen til cellen som inneholder tallet du vil finne kvadratroten for.

For eksempel , for å få en kvadratrot av 225, bruker du denne formelen:

=SQRT(225)

For å beregne kvadratroten av et tall i A2, bruk denne:

=SQRT(A2)

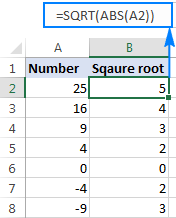
Hvis et tall er negativt, som i rad 7 og 8 i skjermbildet ovenfor, returnerer Excel SQRT-funksjonen #NUM! feil. Det skjer fordi kvadratroten av et negativt tall ikke eksisterer blant settet med reelle tall. Hvorfor det? Siden det ikke er mulig å kvadrere et tall og få et negativt resultat.

Hvis du ønsker å ta kvadratroten av et negativt tall som om det var et positivt tall, pakk inn kildenummer i ABS-funksjonen, som returnerer den absolutte verdien av et tall uten hensyn til fortegnet:

=SQRT(ABS(A2))

How to do squarerot i Excel ved hjelp av en beregning

Ved beregning for hånd skriver du kvadratrot ved å bruke det radikale symbolet (√). Selv om det ikke er mulig å skrive det tradisjonelle kvadratrotsymbolet i Excel, er det en måte å finne kvadratrot uten noen funksjon. Til dette bruker du indikatortegnet (^), som er plassert over tallet 6 på de fleste tastaturer.

I Microsoft Excel fungerer indikatorsymbolet (^) som eksponent, eller potens, operator. For eksempel, for å kvadrere tallet 5, dvs. heve 5 til potensen 2, skriver du =5^2 i en celle, som tilsvarer 52.

For å få en kvadratrot, bruk indikatoren med (1/2) eller 0,5 som eksponent:

eller

For eksempel til få kvadratroten av 25, du skriver =25^(1/2) eller =25^0.5 i en celle.

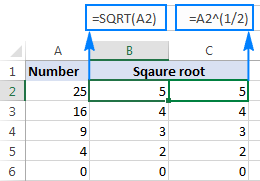
For å finne kvadratroten av et tall i A2, skriver du: =A2^(1/2) eller =A2^0.5

Som vist på skjermbildet nedenfor , Excel SQRT-funksjonen og eksponentformelen gir identiske resultater:

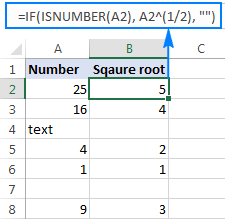
Dette kvadratrotuttrykket kan også brukes som en del av større formler. For eksempel, den følgende IF-setningen forteller Excel å beregne en kvadratrot på betingelse: få en kvadratrot hvis A2 inneholder et tall, men returner en tom streng (tom celle) hvis A2 er en tekstverdi eller tom:

=IF(ISNUMBER(A2), A2^(1/2), "")

Hvorfor er en eksponent av 1/2 det samme som kvadratrot?

For det første, hva kaller vi en kvadratrot? Det er ikke annet enn entall som, multiplisert med seg selv, gir det opprinnelige tallet. For eksempel er kvadratroten av 25 5 fordi 5x5=25. Det er krystallklart, er det ikke?

Vel, å multiplisere 251/2 med seg selv gir også 25:

25½ x 25½ = 25(½+½) = 25(1) = 25

Sagt på en annen måte:

√ 25 x √ 25 = 25

Og:

25½ x 25½ = 25

Så , 25½ tilsvarer √ 25 .

Hvordan finne kvadratrot med POWER-funksjonen

POWER-funksjonen er bare en annen måte å utføre beregningen ovenfor, dvs. heve et tall til potensen 1 /2.

Syntaksen til Excel POWER-funksjonen er som følger:

Som du lett kan gjette, for å få en kvadratrot, leverer du 1/2 til argumentet makt . For eksempel:

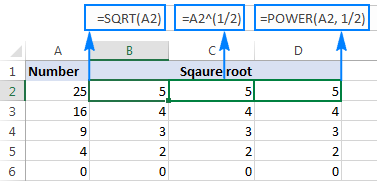
=POWER(A2, 1/2)

Som vist på skjermbildet nedenfor, gir alle tre kvadratrotformlene identiske resultat, hvilken du skal bruke er et spørsmål om din personlige preferanse:

Hvordan beregne N-te rot i Excel

Eksponentformelen diskutert noen få avsnitt ovenfor er ikke begrenset til bare å finne en kvadratrot. De samme teknikkene kan brukes for å få en hvilken som helst n-te rot - bare skriv inn ønsket rot i nevneren til en brøk etter tegnet:

Hvor nummer er tallet du vil finne roten til og n er roten.

For eksempel:

• Terningsroten av 64 vil bli skrevet som: =64^(1/3)
• For å få den 4.roten av 16, skriver du: =16^(1/4)
• For å finne den 5. roten av et tall i celle A2, skriver du: =A2^(1/5)

I stedet for brøker kan du bruke desimaltall i eksponenter, selvfølgelig hvis desimalformen til brøken har et rimelig antall desimaler. For å beregne den fjerde roten av 16, kan du for eksempel bruke enten =16^(1/4) eller =16^0,25.

Vær oppmerksom på at brøkeksponenter alltid skal være vedlagt i parentes for å sikre riktig rekkefølge av operasjoner i kvadratrotformelen - første divisjon (skråstreken (/) er divisjonsoperatoren i Excel), og deretter heve til potensen.

De samme resultatene kan oppnås ved å bruke POWER-funksjonen:

• Terningsroten av 64: =POWER(64, 1/3)
• Den 4. roten av 16: =POWER(16, 1/4)
• Den 5. roten av et tall i celle A2: =POWER(A2, 1/5)

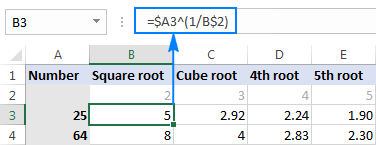
I dine virkelige regneark, du kan skrive inn røttene i separate celler, og referere til disse cellene i formlene dine. Slik finner du for eksempel rotinngangen i B2 til tallet i A3:

=$A3^(1/B$2)

Skjermbildet nedenfor viser resultatene avrundet til 2 desimaler:

Tips. For å utføre flere beregninger med en enkelt formel som i eksemplet ovenfor, fikser du en kolonne- og/eller radreferanse ved å bruke dollartegnet ($). For mer informasjon, se Hvorfor bruke dollartegn i Excelformler.

Slik kan du gjøre kvadratrot i Excel. Jeg takker for at du leser og håper å se deg på bloggen vår neste uke!