Mae'r tiwtorial yn dangos sut i wneud ail isradd yn Excel yn ogystal â sut i gyfrifo Nfed gwraidd unrhyw werth.

Mae sgwario rhif a chymryd ail isradd yn weithrediadau cyffredin iawn yn mathemateg. Ond sut mae gwneud gwraidd sgwâr yn Excel? Naill ai trwy ddefnyddio'r swyddogaeth SQRT neu drwy godi rhif i bŵer 1/2. Mae'r enghreifftiau canlynol yn dangos manylion llawn.

Y ffordd hawsaf o wneud ail isradd yn Excel yw trwy ddefnyddio'r ffwythiant a ddyluniwyd yn arbennig ar gyfer hyn:

Ble rhif yw'r rhif neu'r cyfeiriad at y gell sy'n cynnwys y rhif yr ydych am ddod o hyd i'r ail isradd ar ei gyfer.

Er enghraifft , i gael ail isradd sgwâr o 225, rydych yn defnyddio'r fformiwla hon:

=SQRT(225)

I gyfrifo ail isradd rhif yn A2, defnyddiwch yr un hwn:

=SQRT(A2) <3

Os yw rhif yn negatif, fel yn rhesi 7 ac 8 yn y ciplun uchod, mae ffwythiant Excel SQRT yn dychwelyd y #NUM! gwall. Mae'n digwydd oherwydd nad yw ail isradd rhif negatif yn bodoli ymhlith y set o rifau real. Pam hynny? Gan nad oes unrhyw ffordd i sgwario rhif a chael canlyniad negatif.

Rhag ofn eich bod am gymryd ail isradd o rhif negyddol fel petai'n rhif positif, lapiwch y rhif ffynhonnell yn y ffwythiant ABS, sy'n dychwelyd gwerth absoliwt rhif heb ystyried ei arwydd:

=SQRT(ABS(A2))

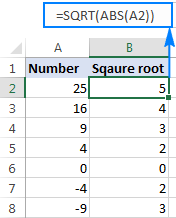
Sut i wneud sgwârgwraidd yn Excel gan ddefnyddio cyfrifiad

Wrth gyfrifo â llaw, rydych yn ysgrifennu ail isradd gan ddefnyddio'r symbol radical (√). Er, nid yw'n bosibl teipio'r symbol gwraidd sgwâr traddodiadol hwnnw yn Excel, mae yna ffordd i ddod o hyd i wraidd sgwâr heb unrhyw swyddogaeth. Ar gyfer hyn, rydych chi'n defnyddio'r nod caret (^), sydd wedi'i leoli uwchben y rhif 6 ar y rhan fwyaf o fysellfyrddau.

Yn Microsoft Excel, mae'r symbol caret (^) yn gweithredu fel yr esboniwr, neu'r gweithredwr pŵer. Er enghraifft, i sgwario'r rhif 5, h.y. codi 5 i bŵer 2, rydych chi'n teipio =5^2 mewn cell, sy'n cyfateb i 52.

I gael ail isradd, defnyddiwch y caret gyda (1/2) neu 0.5 fel yr esboniwr:

neu

Er enghraifft, i cael gwreiddyn sgwâr 25, rydych chi'n teipio =25^(1/2) neu =25^0.5 mewn cell.

I ddod o hyd i ail isradd rhif yn A2, rydych chi'n teipio: =A2^(1/2) neu =A2^0.5

Fel y dangosir yn y ciplun isod , mae'r ffwythiant Excel SQRT a'r fformiwla esboniwr yn rhoi canlyniadau unfath:

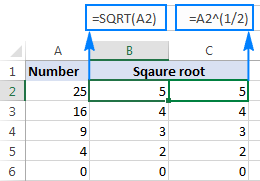
Gellir defnyddio'r mynegiad gwraidd sgwâr hwn hefyd fel rhan o fformiwlâu mwy. Er enghraifft, mae'r datganiad IF canlynol yn dweud wrth Excel i gyfrifo gwreiddyn sgwâr ar gyflwr: cael ail isradd os yw A2 yn cynnwys rhif, ond dychwelyd llinyn gwag (cell wag) os yw A2 yn werth testun neu'n wag:

=IF(ISNUMBER(A2), A2^(1/2), "")

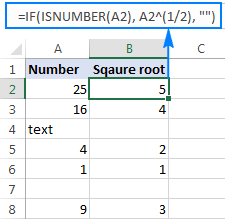
Pam mae esboniwr o 1/2 yr un peth â gwreiddyn sgwâr?

I ddechreuwyr, beth ydyn ni'n ei alw'n ail isradd? Nid yw yn ddim arall ond arhif sydd, o'i luosi ag ef ei hun, yn rhoi'r rhif gwreiddiol. Er enghraifft, gwreiddyn sgwâr 25 yw 5 oherwydd 5x5=25. Mae hynny'n grisial glir, onid yw?

Wel, mae lluosi 251/2 ar ei ben ei hun hefyd yn rhoi 25:

25½ x 25½ = 25(½+½) = 25(1) = 25

Dywedodd ffordd arall:

√ 25 x √ 25 = 25

Ac:

25½ x 25½ = 25

Felly , mae 25½ yn cyfateb i √ 25 .

Sut i ddarganfod ail isradd gyda ffwythiant POWER

Dim ond ffordd arall o wneud y cyfrifiad uchod yw'r ffwythiant POWER, h.y. codi rhif i bŵer 1 /2.

Mae cystrawen ffwythiant Excel POWER fel a ganlyn:

Fel y gallwch chi ddyfalu'n hawdd, i gael gwreiddyn sgwâr, rydych chi'n cyflenwi 1/2 i y ddadl pŵer . Er enghraifft:

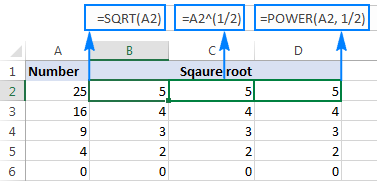
=POWER(A2, 1/2)

Fel y dangosir yn y sgrinlun isod, mae pob un o'r tair fformiwla gwraidd sgwâr yn cynhyrchu canlyniad union yr un fath, pa un i'w ddefnyddio sy'n fater o'ch dewis personol:

Sut i gyfrifo Nfed gwraidd yn Excel

Nid yw'r fformiwla esboniwr a drafodwyd ychydig o baragraffau uchod wedi'i chyfyngu i ddod o hyd i ail isradd yn unig. Gellir defnyddio'r un technegau i gael unrhyw nfed gwreiddyn - teipiwch y gwreiddyn a ddymunir yn enwadur ffracsiwn ar ôl y nod caret:

Ble rhif yw'r rhif yr hoffech chi ddod o hyd i'r gwraidd ohono a n yw'r gwraidd.

Er enghraifft:

• Byddai gwreiddyn ciwb 64 yn cael ei ysgrifennu fel: =64^(1/3)
• I gael y 4yddgwraidd 16, rydych chi'n teipio: = 16 ^ (1/4)
• I ddod o hyd i 5ed gwreiddyn rhif yng nghell A2, rydych chi'n teipio: =A2 ^(1/5)

Yn lle ffracsiynau, gallwch ddefnyddio rhifau degol mewn esbonyddion, wrth gwrs os oes gan ffurf degol y ffracsiwn nifer rhesymol o leoedd degol. Er enghraifft, i gyfrifo'r 4ydd gwreiddyn o 16, gallwch fynd gyda naill ai =16^(1/4) neu =16^0.25.

Sylwch y dylai esbonyddion ffracsiynol fod bob amser wedi'i amgáu mewn cromfachau i sicrhau trefn gywir y gweithrediadau yn eich fformiwla isradd sgwâr - rhaniad cyntaf (y blaenslaes (/) yw gweithredwr y rhaniad yn Excel), ac yna'n codi i'r pŵer.

• Gwreiddyn ciwb 64: =POWER(64, 1/3)
• 4ydd gwreiddyn 16: =POWER(16, 1/4)
• 5ed gwreiddyn rhif yng nghell A2: =POWER(A2, 1/5)

Yn eich taflenni gwaith bywyd go iawn, gallwch deipio'r gwreiddiau mewn celloedd ar wahân, a chyfeirio'r celloedd hynny yn eich fformiwlâu. Er enghraifft, dyma sut rydych chi'n dod o hyd i fewnbwn gwraidd yn B2 y rhif yn A3:

=$A3^(1/B$2)

Mae'r sgrinlun isod yn dangos y canlyniadau wedi'u talgrynnu i 2 le degol:

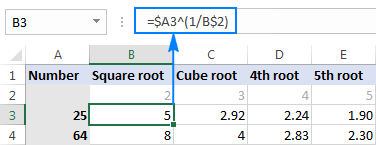
Awgrym. I wneud cyfrifiadau lluosog gydag un fformiwla fel yn yr enghraifft uchod, gosodwch gyfeirnod colofn a/neu res lle bo'n briodol gan ddefnyddio'r arwydd doler ($). Am ragor o wybodaeth, gweler Pam defnyddio arwydd doler yn Excelfformiwlâu.

Dyma sut y gallwch chi wneud ail isradd yn Excel. Diolch i chi am ddarllen a gobeithio gweld chi ar ein blog wythnos nesaf!