Водич показује како да направите квадратни корен у Екцел-у, као и како да израчунате Н-ти корен било које вредности.

Квадрирање броја и узимање квадратног корена су веома уобичајене операције у математика. Али како направити квадратни корен у Екцелу? Или коришћењем функције СКРТ или подизањем броја на степен 1/2. Следећи примери показују све детаље.

Како да извршите квадратни корен у Екцел-у користећи СКРТ функцију

Најлакши начин да направите квадратни корен у Екцел-у је коришћење функције посебно дизајниране за ово:

Где је број број или референца на ћелију која садржи број за који желите да пронађете квадратни корен.

На пример , да бисте добили квадратни корен од 225, користите ову формулу:

=SQRT(225)

Да бисте израчунали квадратни корен из броја у А2, користите ову:

=SQRT(A2)

Ако је број негативан, као у редовима 7 и 8 на слици изнад, Екцел СКРТ функција враћа #НУМ! грешка. То се дешава зато што квадратни корен негативног броја не постоји међу скупом реалних бројева. Зашто је то? Пошто не постоји начин да се број квадрира и добије негативан резултат.

У случају да желите да узмете квадратни корен од негативног броја као да је позитиван број, умотајте изворни број у АБС функцији, који враћа апсолутну вредност броја без обзира на његов знак:

=SQRT(ABS(A2))

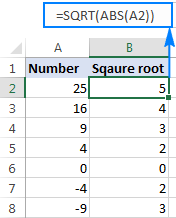
Како се прави квадраткорен у Екцел-у помоћу прорачуна

Када рачунате ручно, квадратни корен пишете помоћу радикалног симбола (√). Иако није могуће откуцати тај традиционални симбол квадратног корена у Екцел-у, постоји начин да пронађете квадратни корен без икакве функције. За ово користите знак за уметање (^), који се налази изнад броја 6 на већини тастатура.

У Мицрософт Екцел-у, симбол курсора (^) делује као оператор експонента или степена. На пример, да бисте квадрирали број 5, тј. повећали 5 на степен од 2, у ћелију укуцавате =5^2, што је еквивалентно 52.

Да бисте добили квадратни корен, користите знак за уметак са (1/2) или 0,5 као експонент:

или

На пример, да да добијете квадратни корен од 25, унесите =25^(1/2) или =25^0.5 у ћелију.

Да бисте пронашли квадратни корен броја у А2, укуцајте: =A2^(1/2) или =A2^0.5

Као што је приказано на снимку екрана испод , Екцел СКРТ функција и формула експонента дају идентичне резултате:

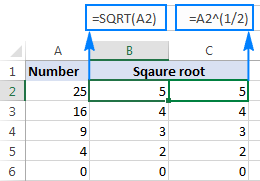
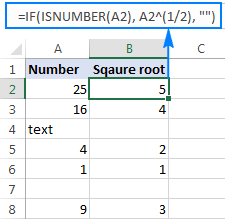
Овај израз квадратног корена се такође може користити као део већих формула. На пример, следећа ИФ изјава говори Екцел-у да израчуна квадратни корен под условом: добије квадратни корен ако А2 садржи број, али врати празан стринг (празна ћелија) ако је А2 текстуална вредност или празно:

=IF(ISNUMBER(A2), A2^(1/2), "")

Зашто је експонент од 1/2 исти као квадратни корен?

За почетак, како зовемо квадратни корен? То није ништа друго него аброј који, када се помножи сам са собом, даје првобитни број. На пример, квадратни корен од 25 је 5 јер је 5к5=25. То је кристално јасно, зар не?

Па, множење 251/2 само по себи такође даје 25:

25½ к 25½ = 25(½+½) = 25(1) = 25

Речено на други начин:

√ 25 к √ 25 = 25

И:

25½ к 25½ = 25

Дакле , 25½ је еквивалентно √ 25 .

Како пронаћи квадратни корен помоћу функције ПОВЕР

Функција ПОВЕР је само још један начин да се изврши горњи прорачун, тј. подигните број на степен од 1 /2.

Синтакса функције Екцел ПОВЕР је следећа:

Као што можете лако да претпоставите, да бисте добили квадратни корен, уносите 1/2 до аргумент повер . На пример:

=POWER(A2, 1/2)

Као што је приказано на слици испод, све три формуле квадратног корена дају идентичан резултат, а коју ћете користити је ствар ваших личних преференција:

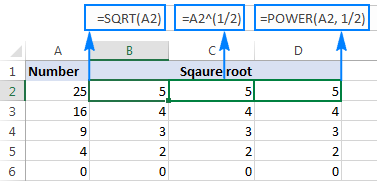
Како израчунати Н-ти корен у Екцел-у

Формула експонента о којој је било речи у неколико параграфа изнад није ограничена на проналажење само квадратног корена. Исте технике се могу користити за добијање било ког н-тог корена - само унесите жељени корен у именилац разломка после знака за уметање:

Где је број број за који желите да пронађете корен, а н је корен.

На пример:

• Куби корен од 64 би био написан као: =64^(1/3)
• Да бисте добили 4.корен од 16, укуцате: =16^(1/4)
• Да бисте пронашли 5. корен броја у ћелији А2, откуцајте: =А2^(1/5)

Уместо разломака, можете користити децималне бројеве у експонентима, наравно ако децимални облик разломка има разуман број децималних места. На пример, да бисте израчунали 4. корен од 16, можете ићи са =16^(1/4) или =16^0,25.

Имајте на уму да разломни експоненти увек треба да буду затворено у загради да би се обезбедио правилан редослед операција у формули квадратног корена – прво дељење (коса црта (/) је оператор дељења у Екцел-у), а затим подизање на степен.

Исти резултати се могу постићи коришћењем функције ПОВЕР:

• Куби корен од 64: =ПОВЕР(64, 1/3)
• 4. корен од 16: =ПОВЕР(16, 1/4)
• Пети корен броја у ћелији А2: =ПОВЕР(А2, 1/5)

У вашим радним листовима из стварног живота, можете да откуцате корене у одвојеним ћелијама и да упућујете на те ћелије у својим формулама. На пример, ево како ћете пронаћи основни унос у Б2 броја у А3:

=$A3^(1/B$2)

Снимак екрана испод приказује резултате заокружене на 2 децимале:

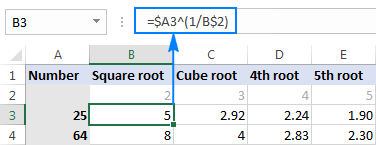
Савет. Да бисте извршили више израчунавања са једном формулом, као у горњем примеру, поправите референцу колоне и/или реда где је то прикладно помоћу знака долара ($). За више информација погледајте Зашто користити знак за долар у Екцел-уформуле.

Овако можете направити квадратни корен у Екцел-у. Захваљујем вам на читању и надам се да се видимо на нашем блогу следеће недеље!