Innehållsförteckning
I handledningen visas hur man räknar ut kvadratroten i Excel och hur man beräknar den n:te roten av ett värde.
Att kvadrera ett tal och ta en kvadratrot är mycket vanliga operationer inom matematiken. Men hur gör man en kvadratrot i Excel? Antingen genom att använda funktionen SQRT eller genom att höja ett tal till en potens av 1/2. Följande exempel visar alla detaljer.
Hur man gör en kvadratrot i Excel med hjälp av SQRT-funktionen
Det enklaste sättet att göra kvadratroten i Excel är att använda den funktion som är speciellt utformad för detta:
SQRT(antal)Var nummer är numret eller referensen till cellen som innehåller det tal för vilket du vill hitta kvadratroten.
För att få fram en kvadratrot av 225 använder du till exempel följande formel:
=SQRT(225)
För att beräkna kvadratroten av ett tal i A2, använd den här:
=SQRT(A2)

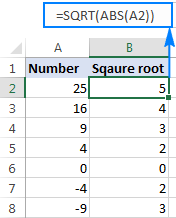
Om ett tal är negativt, som i raderna 7 och 8 i skärmbilden ovan, returnerar Excel-funktionen SQRT felet #NUM! Det beror på att kvadratroten av ett negativt tal inte finns bland de verkliga talen. Varför inte? Eftersom det inte finns något sätt att kvadrera ett tal och få ett negativt resultat.
Om du vill ta en kvadratrot av en negativt tal som om det vore ett positivt tal, och svep in källnumret i ABS-funktionen, som returnerar det absoluta värdet av ett tal utan hänsyn till dess tecken:
=SQRT(ABS(A2))
Hur man gör kvadratroten i Excel med hjälp av en beräkning
När du räknar för hand skriver du kvadratroten med hjälp av radikalsymbolen (√). Även om det inte är möjligt att skriva den traditionella kvadratrotsymbolen i Excel finns det ett sätt att hitta kvadratroten utan någon funktion. För detta använder du karettecknet (^), som finns ovanför siffran 6 på de flesta tangentbord.
I Microsoft Excel fungerar karet-symbolen (^) som exponent- eller potensoperatorn. Om du till exempel vill kvadrera talet 5, dvs. höja 5 till en potens av 2, skriver du =5^2 i en cell, vilket motsvarar 52.
För att få fram en kvadratrot använder du careten med (1/2) eller 0,5 som exponent:
nummer ^(1/2)eller .
nummer ^0.5 För att få fram kvadratroten av 25 skriver du till exempel =25^(1/2) eller . =25^0.5 i en cell.
För att hitta kvadratroten av ett tal i A2 skriver du: =A2^(1/2) eller . =A2^0.5
Som framgår av skärmdumpen nedan ger Excel-funktionen SQRT och exponentformeln identiska resultat:
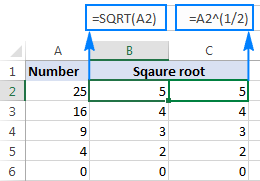
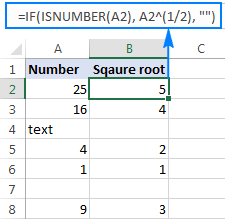
Det här kvadratrotsuttrycket kan också användas som en del av större formler. Följande IF-angivelse säger till exempel till Excel att beräkna en kvadratrot på följande villkor: få en kvadratrot om A2 innehåller ett tal, men återge en tom sträng (tom cell) om A2 är ett textvärde eller tomt:
=IF(ISNUMBER(A2), A2^(1/2), "")
Varför är en exponent på 1/2 samma sak som en kvadratrot?
Till att börja med, vad kallar vi en kvadratrot? Det är inget annat än ett tal som, när det multipliceras med sig självt, ger det ursprungliga talet. Till exempel är kvadratroten av 25 5 eftersom 5x5=25. Det är kristallklart, eller hur?
Om man multiplicerar 251/2 med sig själv får man också 25:
25½ x 25½ = 25(½+½) = 25(1) = 25
På ett annat sätt:
√ 25 x √ 25 = 25
Och:
25½ x 25½ = 25
25½ är alltså likvärdigt med √ 25 .
Hur man hittar kvadratroten med POWER-funktionen
Funktionen POWER är bara ett annat sätt att utföra ovanstående beräkning, dvs. höja ett tal till potensen 1/2.
Syntaxen för Excel POWER-funktionen är följande:
POWER(antal, effekt)Som du lätt kan gissa, för att få fram en kvadratrot, anger du 1/2 till kraft argument. Till exempel:
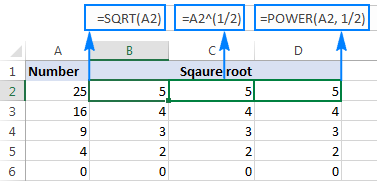
=POWER(A2, 1/2)
Som framgår av skärmbilden nedan ger alla tre formlerna för kvadratroten samma resultat, vilken du ska använda beror på dina personliga preferenser:
Hur man beräknar den n:e roten i Excel
Exponentformeln som vi diskuterade några stycken ovan är inte begränsad till att bara hitta en kvadratrot. Samma teknik kan användas för att få fram vilken nionde rot som helst - skriv bara den önskade roten i bråkets nämnare efter caret-tecknet:
nummer ^(1/ n )Var nummer är det tal som du vill hitta roten till och n är roten.
Till exempel:
- Kubikroten av 64 kan skrivas som: =64^(1/3)
- För att få fram den fjärde roten av 16 skriver du: =16^(1/4)
- För att hitta den femte roten av ett tal i cell A2 skriver du: =A2^(1/5)
I stället för bråk kan du använda decimaltal i exponenter, naturligtvis om bråkets decimalform har ett rimligt antal decimaler. För att beräkna den fjärde roten av 16 kan du till exempel använda antingen =16^(1/4) eller =16^0,25.
Observera att bråkformiga exponenter ska alltid omslutas av parentes för att se till att du har rätt operationsordning i din kvadratrotsformel - först division (skråstrecket (/) är divisionsoperatorn i Excel) och sedan höjning till potens.
Samma resultat kan uppnås genom att använda funktionen POWER:
- Kubikroten av 64: =POWER(64, 1/3)
- Den fjärde roten av 16: =POWER(16, 1/4)
- Den femte roten av ett tal i cell A2: =POWER(A2, 1/5)
I dina verkliga arbetsblad kan du skriva in rötterna i separata celler och hänvisa till dessa celler i dina formler. Så här kan du till exempel hitta rotinmatningen i B2 av talet i A3:
=$A3^(1/B$2)
Skärmbilden nedan visar resultaten avrundade till två decimaler:
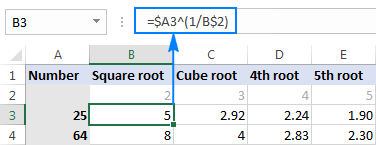
Tips: Om du vill utföra flera beräkningar med en enda formel, som i exemplet ovan, anger du en kolumn- och/eller radreferens där det är lämpligt med hjälp av dollartecknet ($). Mer information finns i Varför använda dollartecken i Excel-formler.
Så här kan du göra kvadratroten i Excel. Tack för att du läste och hoppas att vi ses på vår blogg nästa vecka!

