Vodič pokazuje kako napraviti kvadratni korijen u Excelu, kao i kako izračunati N-ti korijen bilo koje vrijednosti.

Kvadriranje broja i uzimanje kvadratnog korijena vrlo su uobičajene operacije u matematike. Ali kako napraviti kvadratni korijen u Excelu? Ili korištenjem SQRT funkcije ili podizanjem broja na stepen 1/2. Sljedeći primjeri pokazuju potpune detalje.

Kako napraviti kvadratni korijen u Excelu koristeći SQRT funkciju

Najlakši način da napravite kvadratni korijen u Excelu je korištenje funkcije posebno dizajnirane za ovo:

Gdje je broj broj ili referenca na ćeliju koja sadrži broj za koji želite pronaći kvadratni korijen.

Na primjer , da biste dobili kvadratni korijen od 225, koristite ovu formulu:

=SQRT(225)

Da biste izračunali kvadratni korijen broja u A2, koristite ovu:

=SQRT(A2)

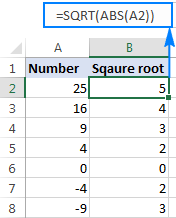
Ako je broj negativan, kao u redovima 7 i 8 na slici iznad, funkcija Excel SQRT vraća #NUM! greška. To se događa zato što kvadratni korijen negativnog broja ne postoji među skupom realnih brojeva. Zašto je to? Pošto ne postoji način da se broj kvadrira i dobije negativan rezultat.

U slučaju da želite uzeti kvadratni korijen od negativnog broja kao da je pozitivan broj, omotajte izvorni broj u ABS funkciji, koja vraća apsolutnu vrijednost broja bez obzira na njegov znak:

=SQRT(ABS(A2))

Kako napraviti kvadratkorijen u Excelu pomoću izračuna

Kada računate ručno, kvadratni korijen pišete pomoću radikalnog simbola (√). Iako nije moguće otkucati taj tradicionalni simbol kvadratnog korijena u Excelu, postoji način da pronađete kvadratni korijen bez ikakve funkcije. Za ovo koristite znak za umetanje (^), koji se nalazi iznad broja 6 na većini tastatura.

U Microsoft Excel-u, znak za umetanje (^) djeluje kao eksponent ili potencijski operator. Na primjer, da kvadrirate broj 5, tj. povisite 5 na stepen 2, u ćeliju ukucate =5^2, što je ekvivalentno 52.

Da biste dobili kvadratni korijen, koristite znak za umetanje sa (1/2) ili 0,5 kao eksponent:

ili

Na primjer, za dobijete kvadratni korijen od 25, upišite =25^(1/2) ili =25^0.5 u ćeliju.

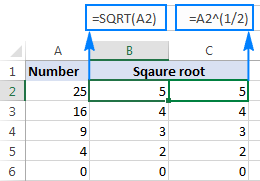
Da biste pronašli kvadratni korijen broja u A2, upišite: =A2^(1/2) ili =A2^0.5

Kao što je prikazano na snimku ekrana ispod , Excel SQRT funkcija i formula eksponenta daju identične rezultate:

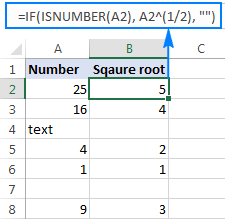
Ovaj izraz kvadratnog korijena također se može koristiti kao dio većih formula. Na primjer, sljedeća IF izjava govori Excelu da izračuna kvadratni korijen pod uslovom: dobije kvadratni korijen ako A2 sadrži broj, ali vrati prazan niz (prazna ćelija) ako je A2 tekstualna vrijednost ili prazno:

=IF(ISNUMBER(A2), A2^(1/2), "")

Zašto je eksponent od 1/2 isti kao kvadratni korijen?

Za početak, kako zovemo kvadratni korijen? To nije ništa drugo nego abroj koji, kada se pomnoži sam sa sobom, daje originalni broj. Na primjer, kvadratni korijen od 25 je 5 jer je 5x5=25. To je kristalno jasno, zar ne?

Pa, množenjem 251/2 sam po sebi dobija se 25:

25½ x 25½ = 25(½+½) = 25(1) = 25

Rečeno na drugi način:

√ 25 x √ 25 = 25

I:

25½ x 25½ = 25

Dakle , 25½ je ekvivalentno √ 25 .

Kako pronaći kvadratni korijen sa POWER funkcijom

Funkcija POWER je samo još jedan način za izvođenje gornjeg izračuna, tj. podići broj na stepen od 1 /2.

Sintaksa funkcije Excel POWER je sljedeća:

Kao što možete lako pogoditi, da biste dobili kvadratni korijen, dajete 1/2 do argument power . Na primjer:

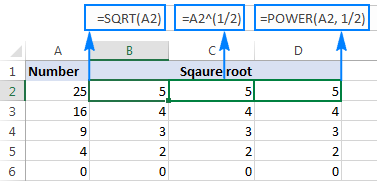
=POWER(A2, 1/2)

Kao što je prikazano na slici ispod, sve tri formule kvadratnog korijena daju identičan rezultat, a koju ćete koristiti je stvar vaših ličnih preferencija:

Kako izračunati N-ti korijen u Excel-u

Formula eksponenta o kojoj se raspravljalo nekoliko paragrafa iznad nije ograničena na pronalaženje samo kvadratnog korijena. Iste tehnike se mogu koristiti za dobivanje bilo kojeg n-tog korijena - samo upišite željeni korijen u nazivnik razlomka nakon znaka za umetanje:

Gdje je broj broj za koji želite pronaći korijen, a n je korijen.

Na primjer:

• Kubni korijen od 64 bi bio napisan kao: =64^(1/3)
• Da bi se dobio 4.korijen od 16, upisujete: =16^(1/4)
• Da biste pronašli 5. korijen broja u ćeliji A2, upišite: =A2^(1/5)

Umjesto razlomaka, možete koristiti decimalne brojeve u eksponentima, naravno ako decimalni oblik razlomka ima razuman broj decimalnih mjesta. Na primjer, da biste izračunali 4. korijen od 16, možete ići sa =16^(1/4) ili =16^0,25.

Molimo primijetite da razlomni eksponenti uvijek trebaju biti zatvoreno u zagradu kako bi se osigurao pravilan redoslijed operacija u vašoj formuli kvadratnog korijena - prvo dijeljenje (kosa crta (/) je operator dijeljenja u Excelu), a zatim podizanje na stepen.

Isti rezultati se mogu postići korištenjem funkcije POWER:

• Kubi korijen od 64: =POWER(64, 1/3)
• 4. korijen od 16: =POWER(16, 1/4)
• Peti korijen broja u ćeliji A2: =POWER(A2, 1/5)

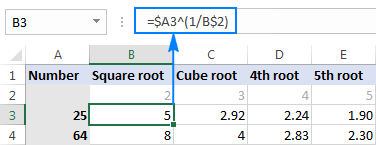
U vašim radnim listovima iz stvarnog života, možete upisati korijene u zasebne ćelije i referencirati te ćelije u svojim formulama. Na primjer, evo kako ćete pronaći korijenski unos u B2 broja u A3:

=$A3^(1/B$2)

Snimak ekrana ispod prikazuje rezultate zaokružene na 2 decimale:

Savjet. Da biste izvršili više izračunavanja s jednom formulom, kao u gornjem primjeru, popravite referencu stupca i/ili reda gdje je to prikladno pomoću znaka dolara ($). Za više informacija pogledajte Zašto koristiti znak za dolar u Exceluformule.

Ovako možete napraviti kvadratni korijen u Excelu. Zahvaljujem vam na čitanju i nadam se da se vidimo na našem blogu sljedeće sedmice!