Enhavtabelo
La lernilo montras kiel fari kvadratan radikon en Excel kaj ankaŭ kiel kalkuli N-an radikon de iu ajn valoro.
Kvadrado de nombro kaj preni kvadratan radikon estas tre oftaj operacioj en matematiko. Sed kiel vi faras kvadratan radikon en Excel? Aŭ uzante la SQRT-funkcion aŭ levante nombron al la potenco de 1/2. La sekvaj ekzemploj montras plenajn detalojn.
Kiel kvadrati radikon en Excel per SQRT-funkcio
La plej facila maniero fari kvadratan radikon en Excel estas uzi la funkcion speciale desegnitan por tio:
SQRT(nombro)Kie numero estas la nombro aŭ referenco al la ĉelo enhavanta la nombron por kiu vi volas trovi la kvadratan radikon.
Ekzemple , por akiri kvadratan radikon de 225, vi uzas ĉi tiun formulon:
=SQRT(225)
Por kalkuli kvadratan radikon de nombro en A2, uzu ĉi tiun:
=SQRT(A2)

Se nombro estas negativa, kiel en vicoj 7 kaj 8 en la supra ekrankopio, la Excel SQRT-funkcio redonas la #NUM! eraro. Ĝi okazas ĉar la kvadrata radiko de negativa nombro ne ekzistas inter la aro de reelaj nombroj. Kial tio? Ĉar ne ekzistas maniero kvadrati nombron kaj ricevi negativan rezulton.
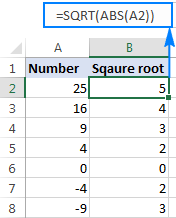
Se vi volas preni kvadratan radikon de negativa nombro kvazaŭ ĝi estus pozitiva nombro, envolvu la fontnumero en la ABS-funkcio, kiu resendas la absolutan valoron de nombro sen konsidero de ĝia signo:
=SQRT(ABS(A2))
Kiel fari kvadratonradiko en Excel uzante kalkulon
Dum kalkulo mane, oni skribas kvadratan radikon per la radikala simbolo (√). Tamen, ne eblas tajpi tiun tradician kvadratan radikan simbolon en Excel, ekzistas maniero trovi kvadratan radikon sen ajna funkcio. Por tio, vi uzas la signon (^), kiu troviĝas super la numero 6 ĉe la plej multaj klavaroj.
En Microsoft Excel, la signo signo (^) funkcias kiel la eksponento, aŭ potenco, funkciigisto. Ekzemple, por kvadratigi la nombron 5, t.e. altigi 5 al la potenco de 2, vi tajpu =5^2 en ĉelo, kio estas ekvivalenta al 52.
Por akiri kvadratan radikon, uzu la signon kun (1/2) aŭ 0,5 kiel la eksponento:
nombro^(1/2)aŭ
nombro^0,5 Ekzemple, al akiru la kvadratan radikon de 25, vi tajpas =25^(1/2) aŭ =25^0.5 en ĉelo.
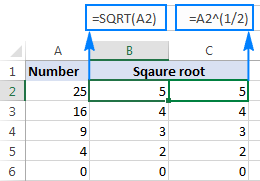
Por trovi kvadratan radikon de nombro en A2, vi tajpu: =A2^(1/2) aŭ =A2^0.5
Kiel montrite en la suba ekrankopio , la Excel SQRT-funkcio kaj la eksponenta formulo donas identajn rezultojn:
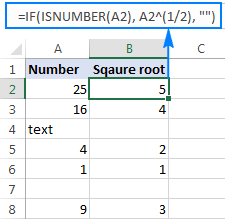
Ĉi tiu kvadratradika esprimo ankaŭ povas esti uzata kiel parto de pli grandaj formuloj. Ekzemple, la sekva IF-aserto diras al Excel kalkuli kvadratan radikon kondiĉe: ricevi kvadratan radikon se A2 enhavas nombron, sed redonu malplenan ĉenon (malplena ĉelo) se A2 estas teksta valoro aŭ malplena:
=IF(ISNUMBER(A2), A2^(1/2), "")
Kial eksponento de 1/2 estas sama kiel kvadrata radiko?
Por komenci, kiel ni nomas kvadrata radiko? Ĝi estas nenio alia ol anombro kiu, multiplikita per si mem, donas la originan nombron. Ekzemple, la kvadrata radiko de 25 estas 5 ĉar 5x5=25. Tio estas kristale klara, ĉu ne?
Nu, multiplikante 251/2 per si mem ankaŭ donas 25:
25½ x 25½ = 25(½+½) = 25(1) = 25
Dirite alimaniere:
√ 25 x √ 25 = 25
Kaj:
25½ x 25½ = 25
Do , 25½ estas ekvivalenta al √ 25 .
Kiel trovi kvadratan radikon per potenca funkcio
La potenca funkcio estas nur alia maniero fari la ĉi-supran kalkulon, t.e. levi nombron al la potenco de 1 /2.
La sintakso de la Excel POWER-funkcio estas jena:
POWER(nombro, potenco)Kiel vi povas facile diveni, por akiri kvadratan radikon, vi provizas 1/2 al la povo argumento. Ekzemple:
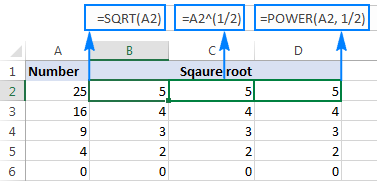
=POWER(A2, 1/2)
Kiel montrite en la malsupra ekrankopio, ĉiuj tri kvadratradikaj formuloj produktas identan rezulton, kiun uzi estas demando de via persona prefero:
Kiel kalkuli N-an radikon en Excel
La eksponenta formulo diskutita kelkajn alineojn supre ne estas limigita al trovi nur kvadratan radikon. La samaj teknikoj povas esti uzataj por ricevi ajnan n-an radikon - simple tajpu la deziratan radikon en la denominatoro de frakcio post la kamero:
numero^(1/ n)Kie numero estas la nombro de kiu vi ŝatus trovi la radikon kaj n estas la radiko.
Ekzemple:
- La kuba radiko de 64 estus skribita kiel: =64^(1/3)
- Por akiri la 4-anradiko de 16, vi tajpu: =16^(1/4)
- Por trovi la 5-an radikon de nombro en ĉelo A2, vi tajpu: =A2^(1/5)
Anstataŭ frakcioj, vi povas uzi decimalnombrojn en eksponentoj, kompreneble se la dekuma formo de la frakcio havas racian nombron da decimalaj lokoj. Ekzemple, por kalkuli la 4-an radikon de 16, vi povas iri kun aŭ =16^(1/4) aŭ =16^0.25.
Bonvolu rimarki, ke frakciaj eksponentoj devus ĉiam esti enfermita en parentezo por certigi la ĝustan ordon de operacioj en via kvadratradika formulo - unua divido (la antaŭen oblikvo (/) estas la divida operatoro en Excel), kaj poste altiĝo al la potenco.
La samaj rezultoj povas esti atingitaj per la funkcio POWER:
- La kuba radiko de 64: =POTENCO(64, 1/3)
- La 4-a radiko de 16: =POTENCO(16, 1/4)
- La 5-a radiko de nombro en ĉelo A2: =POTENCO(A2, 1/5)
En viaj realvivaj laborfolioj, vi povas tajpi la radikojn en apartaj ĉeloj, kaj referenci tiujn ĉelojn en viaj formuloj. Ekzemple, jen kiel vi trovas la radikan enigon en B2 de la nombro en A3:
=$A3^(1/B$2)
La ekrankopio malsupre montras la rezultojn rondigitajn al 2 decimalaj lokoj:
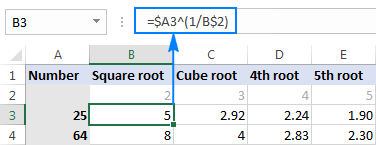
Konsileto. Por fari plurajn kalkulojn kun ununura formulo kiel en la supra ekzemplo, fiksu kolumnon kaj/aŭ vican referencon kie konvene uzante la dolaran signon ($). Por pliaj informoj, bonvolu vidi Kial uzi dolaran signon en Excelformuloj.
Jen kiel vi povas fari kvadratan radikon en Excel. Mi dankas vin pro legado kaj esperas vidi vin en nia blogo venontsemajne!

