INHOUDSOPGAWE
Die tutoriaal wys hoe om vierkantswortel in Excel te doen, asook hoe om Nde wortel van enige waarde te bereken.
Om 'n getal te kwadraat en 'n vierkantswortel te neem is baie algemene bewerkings in wiskunde. Maar hoe doen jy vierkantswortel in Excel? Of deur die SQRT-funksie te gebruik of deur 'n getal tot die mag van 1/2 te verhoog. Die volgende voorbeelde toon volledige besonderhede.
Hoe om vierkantswortel in Excel met behulp van SQRT-funksie
Die maklikste manier om vierkantswortel in Excel te doen, is deur die funksie wat spesiaal ontwerp is te gebruik hiervoor:
SQRT(getal)Waar getal die getal of verwysing na die sel is wat die getal bevat waarvoor jy die vierkantswortel wil vind.
Byvoorbeeld , om 'n vierkantswortel van 225 te kry, gebruik jy hierdie formule:
=SQRT(225)
Om vierkantswortel van 'n getal in A2 te bereken, gebruik hierdie een:
=SQRT(A2)

As 'n getal negatief is, soos in rye 7 en 8 in die skermkiekie hierbo, gee die Excel SQRT-funksie die #NUM! fout. Dit gebeur omdat die vierkantswortel van 'n negatiewe getal nie tussen die stel reële getalle bestaan nie. Hoekom is dit so? Aangesien daar geen manier is om 'n getal te kwadraat en 'n negatiewe resultaat te kry nie.
In geval jy 'n vierkantswortel van 'n negatiewe getal wil neem asof dit 'n positiewe getal is, draai die bronnommer in die ABS-funksie, wat die absolute waarde van 'n getal gee sonder inagneming van sy teken:
=SQRT(ABS(A2))
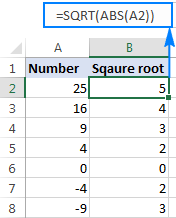
Hoe om vierkant te doenwortel in Excel deur 'n berekening te gebruik
Wanneer jy met die hand bereken, skryf jy vierkantswortel deur die radikale simbool (√) te gebruik. Alhoewel dit nie moontlik is om daardie tradisionele vierkantswortelsimbool in Excel te tik nie, is daar 'n manier om vierkantswortel sonder enige funksie te vind. Hiervoor gebruik jy die karetkarakter (^), wat bokant die nommer 6 op die meeste sleutelborde geleë is.
In Microsoft Excel tree die karetsimbool (^) op as die eksponent, of krag, operateur. Byvoorbeeld, om die getal 5 kwadraat te maak, dit wil sê om 5 tot die mag van 2 te verhoog, tik jy =5^2 in 'n sel, wat gelykstaande is aan 52.
Om 'n vierkantswortel te kry, gebruik die karet met (1/2) of 0.5 as die eksponent:
getal^(1/2)of
getal^0.5 Byvoorbeeld, om kry die vierkantswortel van 25, jy tik =25^(1/2) of =25^0.5 in 'n sel.
Om vierkantswortel van 'n getal in A2 te vind, tik jy: =A2^(1/2) of =A2^0.5
Soos getoon in die skermkiekie hieronder , die Excel SQRT-funksie en die eksponentformule lewer identiese resultate:
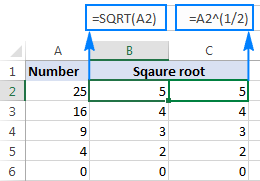
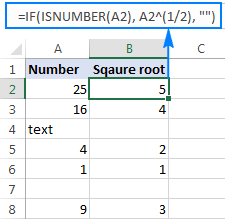
Hierdie vierkantsworteluitdrukking kan ook as deel van groter formules gebruik word. Byvoorbeeld, die volgende IF-stelling sê vir Excel om 'n vierkantswortel te bereken op voorwaarde: kry 'n vierkantswortel as A2 'n getal bevat, maar gee 'n leë string (leë sel) terug as A2 'n tekswaarde of leeg is:
=IF(ISNUMBER(A2), A2^(1/2), "")
Hoekom is 'n eksponent van 1/2 dieselfde as vierkantswortel?
Om mee te begin, wat noem ons 'n vierkantswortel? Dit is niks anders as agetal wat, wanneer dit met homself vermenigvuldig word, die oorspronklike getal gee. Byvoorbeeld, die vierkantswortel van 25 is 5 omdat 5x5=25. Dit is kristalhelder, is dit nie?
Wel, vermenigvuldiging van 251/2 met homself gee ook 25:
25½ x 25½ = 25(½+½) = 25(1) = 25
Op 'n ander manier gesê:
√ 25 x √ 25 = 25
En:
25½ x 25½ = 25
Dus , 25½ is gelykstaande aan √ 25 .
Hoe om vierkantswortel met POWER-funksie te vind
Die POWER-funksie is net nog 'n manier om bogenoemde berekening uit te voer, d.w.s. verhoog 'n getal tot die mag van 1 /2.
Die sintaksis van die Excel POWER-funksie is soos volg:
POWER(getal, mag)Soos jy maklik kan raai, om 'n vierkantswortel te kry, verskaf jy 1/2 aan die krag argument. Byvoorbeeld:
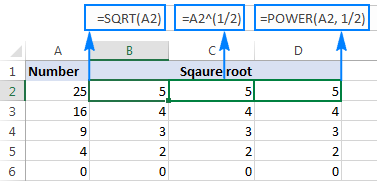
=POWER(A2, 1/2)
Soos in die skermkiekie hieronder getoon, lewer al drie vierkantswortelformules identiese resultate, watter een om te gebruik is 'n kwessie van jou persoonlike voorkeur:
Hoe om Nde wortel in Excel te bereken
Die eksponentformule wat 'n paar paragrawe hierbo bespreek is, is nie beperk tot die vind van slegs 'n vierkantswortel nie. Dieselfde tegnieke kan gebruik word om enige n-de wortel te kry - tik net die verlangde wortel in die noemer van 'n breuk na die karetkarakter:
getal^(1/ n)Waar getal die getal is waarvan jy die wortel wil vind en n die wortel is.
Byvoorbeeld:
- Die derdemagswortel van 64 sal geskryf word as: =64^(1/3)
- Om die 4de te krywortel van 16, tik jy: =16^(1/4)
- Om die 5de wortel van 'n getal in sel A2 te vind, tik jy: =A2^(1/5)
In plaas van breuke, kan jy desimale getalle in eksponente gebruik, natuurlik as die desimale vorm van die breuk 'n redelike aantal desimale plekke het. Byvoorbeeld, om die 4de wortel van 16 te bereken, kan jy met óf =16^(1/4) óf =16^0.25 gaan.
Let asseblief op dat breukeksponente altyd moet wees ingesluit in hakies om die korrekte volgorde van bewerkings in jou vierkantswortelformule te verseker - eerste deling (die voorwaartse skuinsstreep (/) is die delingsoperateur in Excel), en dan verhoog na die mag.
Dieselfde resultate kan bereik word deur die POWER-funksie te gebruik:
- Die derdemagswortel van 64: =POWER(64, 1/3)
- Die 4de wortel van 16: =KRAG(16, 1/4)
- Die 5de wortel van 'n getal in sel A2: =KRAG(A2, 1/5)
In jou werklike werkblaaie, jy kan die wortels in aparte selle tik, en na daardie selle in jou formules verwys. Byvoorbeeld, hier is hoe jy die wortelinvoer in B2 van die getal in A3 vind:
=$A3^(1/B$2)
Die skermkiekie hieronder wys die resultate afgerond tot 2 desimale plekke:
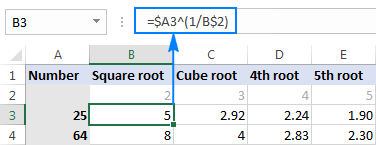
Wenk. Om veelvuldige berekeninge met 'n enkele formule uit te voer soos in die voorbeeld hierbo, stel 'n kolom- en/of ryverwysing vas waar toepaslik deur die dollarteken ($) te gebruik. Vir meer inligting, sien asseblief Waarom dollarteken in Excel gebruikformules.
Dit is hoe jy vierkantswortel in Excel kan doen. Ek bedank jou vir die lees en hoop om jou volgende week op ons blog te sien!

