বিষয়বস্তুৰ তালিকা
টিউটোৰিয়েলটোৱে এক্সেলত ওজনযুক্ত গড় গণনা কৰাৰ দুটা সহজ উপায় প্ৰদৰ্শন কৰিছে - SUM বা SUMPRODUCT ফাংচন ব্যৱহাৰ কৰি।
পূৰ্বৰ এটা প্ৰবন্ধত আমি গণনাৰ বাবে তিনিটা প্ৰয়োজনীয় ফাংচনৰ বিষয়ে আলোচনা কৰিছিলো এক্সেলত গড়, যিবোৰ অতি সহজ আৰু ব্যৱহাৰ কৰাত সহজ। কিন্তু যদি কিছুমান মূল্যৰ আনতকৈ অধিক "ওজন" থাকে আৰু ফলস্বৰূপে চূড়ান্ত গড়ত অধিক অৰিহণা যোগায় তেন্তে কি হ'ব? এনে পৰিস্থিতিত আপুনি ওজনযুক্ত গড় গণনা কৰিব লাগিব।
যদিও মাইক্ৰ'ছফ্ট এক্সেলে বিশেষ ওজনযুক্ত গড় ফাংচন প্ৰদান নকৰে, ইয়াৰ আন দুটামান ফাংচন আছে যিবোৰ আপোনাৰ গণনাত উপযোগী বুলি প্ৰমাণিত হ'ব, যেনে... তাৰ পিছৰ সূত্ৰৰ উদাহৰণত প্ৰদৰ্শন কৰা হৈছে।
ওজনযুক্ত গড় কি?
ওজনযুক্ত গড় হৈছে এক প্ৰকাৰৰ গাণিতিক গড় য'ত কিছুমান উপাদানৰ... তথ্যৰ গোটটোৱে আনতকৈ অধিক গুৰুত্ব বহন কৰে। অৰ্থাৎ গড় ল’বলগীয়া প্ৰতিটো মানক এটা নিৰ্দিষ্ট ওজন দিয়া হয়।
ছাত্ৰ-ছাত্ৰীৰ গ্ৰেড প্ৰায়ে ওজনযুক্ত গড় ব্যৱহাৰ কৰি গণনা কৰা হয়, যিটো তলৰ স্ক্ৰীণশ্বটত দেখুওৱা হৈছে। Excel AVERAGE ফাংচনৰ সহায়ত এটা সাধাৰণ গড় সহজেই গণনা কৰা হয়। কিন্তু আমি বিচাৰো যে গড় সূত্ৰটোৱে C স্তম্ভত তালিকাভুক্ত প্ৰতিটো কাৰ্য্যকলাপৰ ওজন বিবেচনা কৰক।
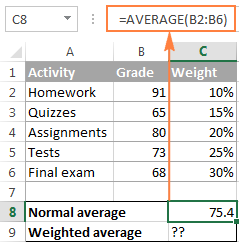
গণিত আৰু পৰিসংখ্যাত আপুনি গোটটোৰ প্ৰতিটো মান গুণ কৰি ওজনযুক্ত গড় গণনা কৰে ইয়াৰ ওজনৰ দ্বাৰা, তাৰ পিছত আপুনি পণ্যসমূহ যোগ কৰে আৰু পণ্যসমূহৰ যোগফলৰ দ্বাৰা ভাগ কৰেএই উদাহৰণত, ওজনযুক্ত গড় (সামগ্ৰিক গ্ৰেড) গণনা কৰিবলৈ, আপুনি প্ৰতিটো গ্ৰেডক সংশ্লিষ্ট শতাংশৰে গুণ কৰে (এটা দশমিকলৈ ৰূপান্তৰ কৰা), ৫টা উৎপাদন একেলগে যোগ কৰে, আৰু সেই সংখ্যাটোক ৫ টা ওজনৰ যোগফলৰে ভাগ কৰক:
((91*0.1)+(65*0.15)+(80*0.2)+(73*0.25)+(68*0.3)) / ( 0.1+0.15+0.2+0.25+0.3)=73.5
আপুনি দেখাৰ দৰে, এটা সাধাৰণ গড় গ্ৰেড (75.4) আৰু ওজনযুক্ত গড় (73.5) বেলেগ বেলেগ মান।
এক্সেলত ওজনযুক্ত গড় গণনা কৰা
মাইক্ৰ'ছফ্ট এক্সেলত, ওজনযুক্ত গড় গণনা কৰা হয় একে পদ্ধতি ব্যৱহাৰ কৰি কিন্তু বহুত কম প্ৰচেষ্টাৰে কাৰণ এক্সেল ফাংচনে আপোনাৰ বাবে বেছিভাগ কাম কৰিব।
SUM ফাংচন ব্যৱহাৰ কৰি ওজনযুক্ত গড় গণনা কৰা
যদি আপোনাৰ Excel SUM ফাংচনৰ মৌলিক জ্ঞান আছে, তেন্তে তলৰ সূত্ৰটোৰ কোনো ব্যাখ্যাৰ প্ৰয়োজন নহ'ব:
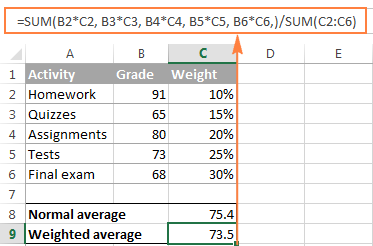
=SUM(B2*C2, B3*C3, B4*C4, B5*C5, B6*C6,)/SUM(C2:C6)
মূলতঃ ই ওপৰত বৰ্ণনা কৰা ধৰণে একে গণনা কৰে, ইয়াৰ বাহিৰে আপুনি সংখ্যাৰ পৰিবৰ্তে ঘৰ প্ৰসংগসমূহ যোগান ধৰে।
যেনেকৈ আপুনি পৰ্দাত চাব পাৰে ot, সূত্ৰটোৱে আমি ক্ষন্তেক আগতে কৰা গণনাৰ দৰেই হুবহু একে ফলাফল দিয়ে। AVERAGE ফাংচন (C8) আৰু ওজনযুক্ত গড় (C9) দ্বাৰা ঘূৰাই দিয়া স্বাভাৱিক গড়ৰ মাজৰ পাৰ্থক্য লক্ষ্য কৰক।
যদিও SUM সূত্ৰটো অতি সহজ আৰু বুজিবলৈ সহজ, ই এটা কাৰ্য্যকৰী বিকল্প নহয় যদি আপোনাৰ গড়লৈ বহু সংখ্যক উপাদান আছে। এই ক্ষেত্ৰত আপুনি ভাল হ’বপৰৱৰ্তী উদাহৰণত দেখুওৱাৰ দৰে SUMPRODUCT ফাংচন ব্যৱহাৰ কৰক।
SUMPRODUCT ৰ সৈতে ওজনযুক্ত গড় বিচাৰি উলিওৱা
Excel ৰ SUMPRODUCT ফাংচন এই কামৰ বাবে একেবাৰে উপযুক্ত কাৰণ ইয়াক উৎপাদনসমূহৰ যোগফল কৰিবলৈ ডিজাইন কৰা হৈছে, যিটো আমাৰ প্ৰয়োজন . গতিকে, প্ৰতিটো মানক ইয়াৰ ওজনেৰে পৃথকে পৃথকে গুণ কৰাৰ পৰিৱৰ্তে, আপুনি SUMPRODUCT সূত্ৰত দুটা এৰে যোগান ধৰে (এই প্ৰসংগত, এটা এৰে হৈছে কোষৰ এটা অবিৰত পৰিসীমা), আৰু তাৰ পিছত ফলাফলটোক ওজনৰ যোগফলৰে ভাগ কৰে:
= SUMPRODUCT( values_range, weights_range) / SUM( weights_range)ধৰি লওক যে গড়লৈ মানসমূহ B2:B6 কোষত আৰু ওজন C2 কোষত আছে: C6, আমাৰ Sumproduct ওজনযুক্ত গড় সূত্ৰই নিম্নলিখিত আকৃতি লয়:
=SUMPRODUCT(B2:B6, C2:C6) / SUM(C2:C6)
এটা এৰেৰ আঁৰৰ প্ৰকৃত মানসমূহ চাবলৈ, সূত্ৰ বাৰত ইয়াক নিৰ্ব্বাচন কৰক আৰু F9 কি' টিপক। ফলাফলটো ইয়াৰ দৰেই হ'ব:
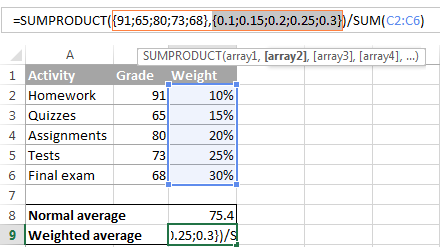
গতিকে, SUMPRODUCT ফাংচনে যি কৰে সেয়া হ'ল array1 ৰ 1st মানক array2 ৰ 1st মানৰে গুণ কৰা (এই উদাহৰণত 91*0.1 ), তাৰ পিছত array1 ৰ 2nd মানটোক array2 ৰ 2nd মানৰে গুণ কৰক (এই উদাহৰণত 65*0.15), ইত্যাদি। যেতিয়া সকলো গুণন কৰা হয়, ফাংচনে উৎপাদকসমূহ যোগ কৰে আৰু সেই যোগফল ঘূৰাই দিয়ে।
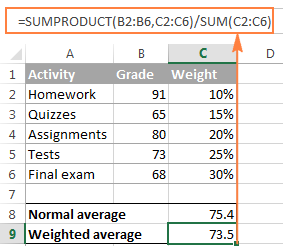
SUMPRODUCT ফাংচনে এটা সঠিক ফলাফল দিয়ে নে নাই সেয়া নিশ্চিত কৰিবলৈ, ইয়াক তুলনা কৰক পূৰ্বৰ উদাহৰণৰ পৰা SUM সূত্ৰ আৰু আপুনি দেখিব যে সংখ্যাবোৰ একে।
ব্যৱহাৰ কৰাৰ সময়তExcel ত ওজনৰ গড় বিচাৰিবলৈ SUM বা SUMPRODUCT ফাংচন কৰক, ওজন ১০০% লৈকে যোগ কৰিব নালাগে। নতুবা সেইবোৰক শতাংশ হিচাপে প্ৰকাশ কৰাৰ প্ৰয়োজন নাই। উদাহৰণস্বৰূপে, আপুনি এটা অগ্ৰাধিকাৰ / গুৰুত্ব স্কেল বনাব পাৰে আৰু প্ৰতিটো বস্তুৰ বাবে এটা নিৰ্দিষ্ট সংখ্যক পইণ্ট নিযুক্ত কৰিব পাৰে, নিম্নলিখিত পৰ্দাশটত প্ৰদৰ্শিত হোৱাৰ দৰে:
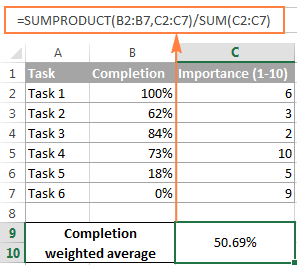
বাৰু, সেইটোৱেই সকলো এক্সেলত ওজনযুক্ত গড় গণনা কৰা। আপুনি তলৰ নমুনা স্প্ৰেডশ্বীট ডাউনলোড কৰিব পাৰে আৰু আপোনাৰ তথ্যত সূত্ৰসমূহ চেষ্টা কৰিব পাৰে। পৰৱৰ্তী টিউটোৰিয়েলত আমি মুভিং এভাৰেজ গণনা কৰাৰ বিষয়ে ভালদৰে চাম। মই আপোনাক পঢ়াৰ বাবে ধন্যবাদ জনাইছো আৰু অহা সপ্তাহত আপোনাক লগ পাবলৈ আগ্ৰহী!
অভ্যাস কাৰ্য্যপুস্তিকা
এক্সেল ওজনযুক্ত গড় - উদাহৰণ (.xlsx ফাইল)

