Efnisyfirlit
Kennslan sýnir hvernig á að nota IPMT aðgerðina í Excel til að finna vaxtahluta reglubundinnar greiðslu á láni eða húsnæðisláni.
Alltaf þegar þú tekur lán, hvort sem það er húsnæðislán, íbúðalán eða bílalán, þarftu að borga til baka þá upphæð sem þú fékkst upphaflega að láni og vexti ofan á. Í einföldu máli eru vextir kostnaður við að nota peninga einhvers (venjulega banka).
Vaxtahluta lánsgreiðslu er hægt að reikna handvirkt með því að margfalda vexti tímabilsins með eftirstöðvunum. En Microsoft Excel hefur sérstaka aðgerð fyrir þetta - IPMT aðgerðina. Í þessari kennslu munum við fara ítarlega í að útskýra setningafræði þess og gefa raunhæf dæmi um formúlur.
Excel IPMT aðgerð - setningafræði og grunnnotkun
IPMT er vaxtagreiðsluaðgerð Excel. Það skilar vaxtaupphæð lánsgreiðslu á tilteknu tímabili, að því gefnu að vextir og heildarupphæð greiðslu séu stöðug á öllum tímabilum.
Til að muna betur nafn fallsins skaltu taka eftir því að "I" stendur fyrir "vexti" og "PMT" fyrir "greiðslu".
Setjafræði IPMT fallsins í Excel er sem hér segir:
IPMT(hlutfall, á, nper, pv, [fv], [gerð ])Hvar:
- Vaxti (áskilið) - fastir vextir á tímabili. Þú getur gefið það upp sem prósentu eða aukastaf.
Til dæmis, ef þú greiðir árlegar greiðslur af láni með árlegrivextir upp á 6 prósent, notaðu 6% eða 0,06 fyrir vexti .
Ef þú greiðir vikulega, mánaðarlega eða ársfjórðungslega skaltu deila ársvextinum með fjölda greiðslutímabila á ári, eins og sýnt er í þessu dæmi. Segjum að ef þú greiðir fjórðungslega af láni með 6 prósenta ársvöxtum, notaðu 6%/4 fyrir vexti .
- Per (áskilið) - tímabilið sem þú vilt reikna vextina fyrir. Það verður að vera heil tala á bilinu 1 til nper .
- Nper (áskilið) - heildarfjöldi greiðslna á líftíma lánsins.
- Pv (áskilið) - núvirði lánsins eða fjárfestingarinnar. Með öðrum orðum, það er höfuðstóll lánsins, þ.e. upphæðin sem þú fékkst að láni.
- Fv (valfrjálst) - framtíðarvirðið, þ. Ef því er sleppt er gefið í skyn að það sé núll (0).
- Tegund (valfrjálst) - tilgreinir hvenær greiðslur eru á gjalddaga:
- 0 eða sleppt - greiðslur eru gerðar í lok hvers tímabils.
- 1 - greiðslur eru gerðar í upphafi hvers tímabils.
Til dæmis, ef þú fékkst $20.000 lán , sem þú þarft að greiða af með árlegum afborgunum á næstu 3 árum með 6% ársvöxtum, þá er hægt að reikna út vaxtahluta 1. árs greiðslu með þessari formúlu:
=IPMT(6%, 1, 3, 20000)
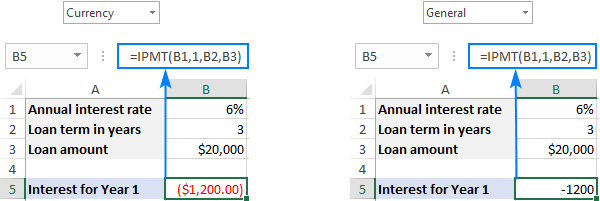
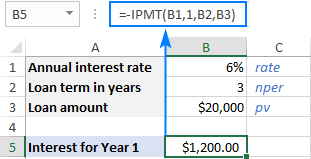
Í stað þess að gefa tölurnar beint inn í formúlu geturðusettu þau inn í fyrirfram skilgreinda reiti og vísaðu til þeirra hólfa eins og sýnt er á skjámyndinni hér að neðan.
Í samræmi við sjóðstreymismerkið er niðurstaðan skilað sem neikvæð númer vegna þess að þú borgar út þessa peninga. Sjálfgefið er að það sé auðkennt með rauðu og lokað innan sviga ( Gjaldmiðill snið fyrir neikvæðar tölur) eins og sýnt er í vinstri hluta skjámyndarinnar hér að neðan. Hægra megin geturðu séð niðurstöðu sömu formúlu á General sniðinu.
Ef þú vilt frekar fá áhuga sem jákvæð tala , settu mínusmerki fyrir annað hvort allt IPMT fallið eða pv rökin:
=-IPMT(6%, 1, 3, 20000)
eða
=IPMT(6%, 1, 3, -20000)
Dæmi um notkun IPMT formúlu í Excel
Nú þegar þú veist grunnatriðin skulum við sjá hvernig á að nota IPMT aðgerðina til að finna vextina fyrir mismunandi greiðslutíðni og hvernig breyting á lánaskilmálum breytir hugsanlegum vöxtum.
Áður en farið er í kaf skal tekið fram að best er að nota IPMT formúlur á eftir PMT fallinu sem reiknar út heildarupphæð tímabils. greiðsla (vextir + höfuðstóll).
IPMT formúla fyrir mismunandi greiðslutíðni (vikur, mánuðir, ársfjórðungar)
Til að fá réttan vaxtahlut af greiðslu láns ættirðu alltaf að umreikna ársvexti hlutfall til samsvarandi tímabils og fjölda ára að heildarfjölda greiðslutímabil:
- Fyrir vextir rökin skaltu deila árlegum vöxtum með fjölda greiðslna á ári, að því gefnu að hið síðarnefnda sé jafnt og fjölda samsettra tímabila á ári.
- Fyrir nper argument , margfaldaðu fjölda ára með fjölda greiðslna á ári.
Eftirfarandi tafla sýnir útreikninga:
| Greiðslutíðni | Rate argument | Nper argument |
| Vikulegar | árlegir vextir hlutfall / 52 | ár * 52 |
| Mánarlega | ársvextir / 12 | ár * 12 |
| Ársfjórðungslega | árlegir vextir / 4 | ár * 4 |
| Hálfárlegt | árlegt vextir / 2 | ár * 2 |
Sem dæmi skulum við finna vextina sem þú þarft að greiða af sama láni en mismunandi greiðslutíðni:
- Ársvextir: 6%
- Lánstími: 2 ár
- Lánsupphæð: $20.000
- Tímabil: 1
Staðan eftir r síðasta greiðsla á að vera $0 ( fv rökinu sleppt), og greiðslur eiga að gjaldfalla í lok hvers tímabils ( type rökinu sleppt).
Vikulega :
=IPMT(6%/52, 1, 2*52, 20000)
Mánaðarlega :
=IPMT(6%/12, 1, 2*12, 20000)
Ársfjórðungslega :
=IPMT(6%/4, 1, 2*4, 20000)
Hálfárlegt :
=IPMT(6%/2, 1, 2*2, 20000)
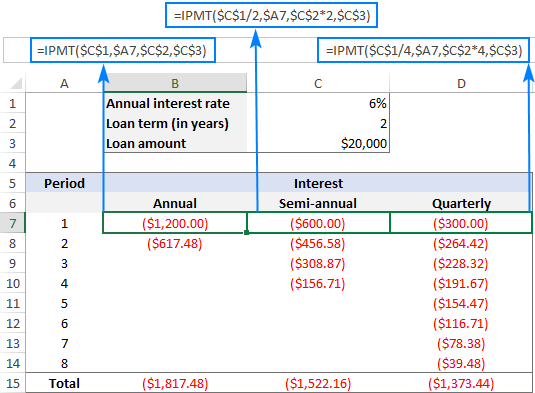
Þegar þú horfir á skjáskotið hér að neðan geturðu tekið eftir því að vaxtaupphæðin minnkar með hverju tímabili á eftir. Þetta ervegna þess að hvers kyns greiðsla stuðlar að lækkun höfuðstóls lánsins og það dregur úr eftirstöðvum sem vextir eru reiknaðir af.
Athugið líka að heildarupphæð vaxta sem greiða þarf af sama láni er mismunandi fyrir árlegt, hálft árlegt. og ársfjórðungslegar afborganir:
Fullt form IPMT fallsins
Í þessu dæmi ætlum við að reikna vexti af sama láni, sömu greiðslutíðni , en mismunandi lífeyristegundir (venjulegar og lífeyrisskyldar). Til þess þurfum við að nota fulla mynd IPMT fallsins.
Til að byrja með skulum við skilgreina inntakshólfin:
- B1 - ársvextir
- B2 - lánstími í árum
- B3 - fjöldi greiðslna á ári
- B4 - lánsfjárhæð ( pv )
- B5 - framtíðarvirði ( fv )
- B6 - þegar greiðslur eru á gjalddaga ( tegund ):
- 0 - í lok tímabils (venjulegur lífeyrir)
- 1 - í upphafi tímabils (lífeyrir)
Að því gefnu að fyrsta tímabilsnúmerið sé í A9, þá er vaxtaformúlan okkar sem hér segir:
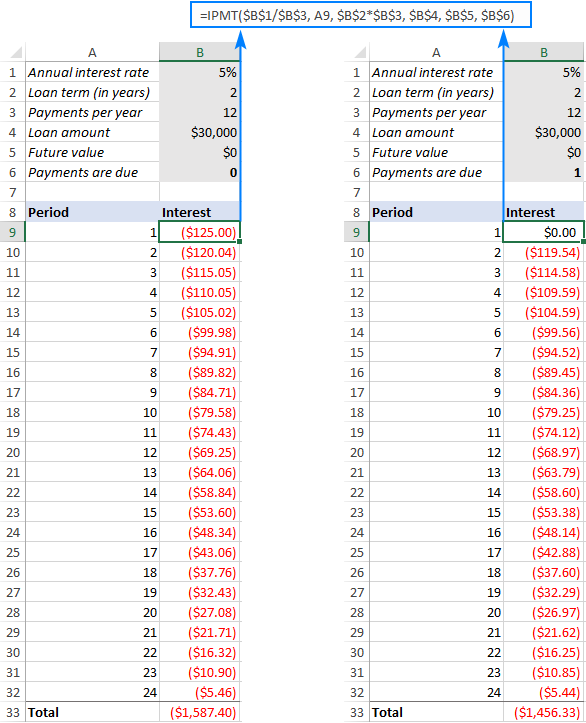
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
Athugið. Ef þú ætlar að nota IPMT formúluna í meira en eitt tímabil, vinsamlegast hafðu í huga frumutilvísanir. Allar tilvísanir í inntakshólfin skulu vera algjörar (með dollaramerkinu) þannig að þær eru læstar við þær hólfa. per rökin verða að vera afstæð frumutilvísun (án dollaramerkja eins og A9) vegna þess að hún ætti að breytast miðað viðhlutfallsleg staða línu sem formúlan er afrituð í.
Svo, við sláum ofangreinda formúlu inn í B9, drögum hana niður fyrir tímabilin sem eftir eru og fáum eftirfarandi niðurstöðu. Ef þú berð saman tölurnar í Vextir dálkunum (venjulegur lífeyrir vinstra megin og lífeyrisskuldbinding hægra megin) muntu taka eftir því að vextir eru aðeins lægri þegar þú greiðir í upphafi tímabils.
Excel IPMT aðgerð virkar ekki
Ef IPMT formúlan þín skilar villu er líklegast að það sé eitt af eftirfarandi:
- #NUM! villa kemur upp er per frumbreytan er utan bilsins 1 til nper .
- #VALUE! villa kemur upp ef einhver rök eru ekki töluleg.
Þannig notarðu IPMT fallið í Excel. Til að skoða betur formúlurnar sem fjallað er um í þessari kennslu er þér velkomið að hlaða niður Excel IPMT virka sýnishorn vinnubók. Ég þakka þér fyrir lesturinn og vonast til að sjá þig á blogginu okkar í næstu viku!

