Mục lục
Hướng dẫn chỉ ra cách sử dụng hàm IPMT trong Excel để tìm phần lãi suất của khoản thanh toán định kỳ đối với khoản vay hoặc thế chấp.
Bất cứ khi nào bạn vay một khoản, cho dù đó là khoản thế chấp, khoản vay mua nhà hay khoản vay mua ô tô, bạn cần phải trả lại số tiền bạn đã vay ban đầu và tiền lãi của khoản vay đó. Nói một cách đơn giản, lãi suất là chi phí sử dụng tiền của ai đó (thường là của ngân hàng).
Phần lãi suất của khoản thanh toán khoản vay có thể được tính toán thủ công bằng cách nhân lãi suất của kỳ hạn với số dư còn lại. Nhưng Microsoft Excel có một chức năng đặc biệt cho việc này - chức năng IPMT. Trong hướng dẫn này, chúng tôi sẽ đi sâu giải thích cú pháp của nó và cung cấp các ví dụ về công thức thực tế.
Hàm IPMT trong Excel - cú pháp và cách sử dụng cơ bản
IPMT là hàm trả lãi của Excel. Hàm trả về số tiền lãi của khoản thanh toán khoản vay trong một khoảng thời gian nhất định, giả sử lãi suất và tổng số tiền khoản thanh toán không đổi trong tất cả các khoảng thời gian.
Để nhớ rõ hơn tên của hàm, hãy lưu ý rằng "I" là viết tắt của cho "lãi" và "PMT" cho "thanh toán".
Cú pháp của hàm IPMT trong Excel như sau:
IPMT(rate, per, nper, pv, [fv], [type ])Ở đâu:
- Tỷ lệ (bắt buộc) - lãi suất không đổi mỗi kỳ. Bạn có thể cung cấp dưới dạng phần trăm hoặc số thập phân.
Ví dụ: nếu bạn thực hiện thanh toán hàng năm cho khoản vay với kỳ hạn hàng nămlãi suất 6 phần trăm, hãy sử dụng 6% hoặc 0,06 cho lãi suất .
Nếu bạn thanh toán hàng tuần, hàng tháng hoặc hàng quý, hãy chia lãi suất hàng năm cho số kỳ thanh toán mỗi năm, như trong ví dụ này. Giả sử, nếu bạn thực hiện thanh toán hàng quý cho khoản vay có lãi suất hàng năm là 6%, hãy sử dụng 6%/4 cho lãi suất .
- Per (bắt buộc) - khoảng thời gian mà bạn muốn tính lãi. Nó phải là một số nguyên trong phạm vi từ 1 đến nper .
- Nper (bắt buộc) - tổng số lần thanh toán trong suốt thời gian vay.
- Pv (bắt buộc) - giá trị hiện tại của khoản vay hoặc khoản đầu tư. Nói cách khác, đó là tiền gốc của khoản vay, tức là số tiền bạn đã vay.
- Fv (tùy chọn) - giá trị tương lai, tức là số dư mong muốn sau lần thanh toán cuối cùng được thực hiện. Nếu bị bỏ qua, nó có nghĩa là không (0).
- Loại (tùy chọn) - chỉ định thời điểm đến hạn thanh toán:
- 0 hoặc bỏ qua - thanh toán được thực hiện vào cuối mỗi kỳ.
- 1 - các khoản thanh toán được thực hiện vào đầu mỗi kỳ.
Ví dụ: nếu bạn nhận khoản vay 20.000 USD , mà bạn phải trả dần hàng năm trong 3 năm tới với lãi suất hàng năm là 6%, phần tiền lãi của khoản thanh toán năm đầu tiên có thể được tính theo công thức sau:
=IPMT(6%, 1, 3, 20000)
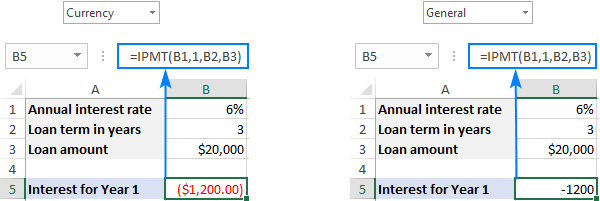
Thay vì cung cấp số trực tiếp vào công thức, bạn có thểnhập chúng vào một số ô được xác định trước và tham chiếu đến các ô đó như trong ảnh chụp màn hình bên dưới.
Theo quy ước về ký hiệu dòng tiền, kết quả được trả về dưới dạng số âm vì bạn thanh toán ra số tiền này. Theo mặc định, nó được đánh dấu bằng màu đỏ và được đặt trong dấu ngoặc đơn (định dạng Tiền tệ cho số âm) như thể hiện ở phần bên trái của ảnh chụp màn hình bên dưới. Ở bên phải, bạn có thể thấy kết quả của cùng một công thức ở định dạng Chung .
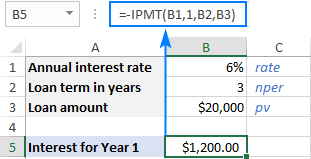
Nếu bạn muốn nhận lãi dưới dạng số dương , đặt dấu trừ trước toàn bộ hàm IPMT hoặc đối số pv :
=-IPMT(6%, 1, 3, 20000)
or
=IPMT(6%, 1, 3, -20000)
Ví dụ về việc sử dụng công thức IPMT trong Excel
Bây giờ bạn đã biết những kiến thức cơ bản, hãy xem cách sử dụng hàm IPMT để tìm số tiền lãi cho các trường hợp khác nhau tần suất thanh toán và việc thay đổi điều kiện khoản vay sẽ thay đổi lãi suất tiềm năng như thế nào.
Trước khi chúng ta đi sâu vào tìm hiểu, cần lưu ý rằng các công thức IPMT tốt nhất nên được sử dụng sau hàm PMT tính toán tổng số tiền của một khoản vay định kỳ. thanh toán (lãi + gốc).
Công thức IPMT cho các tần suất thanh toán khác nhau (tuần, tháng, quý)
Để có được phần lãi của khoản thanh toán khoản vay phù hợp, bạn phải luôn chuyển đổi lãi suất hàng năm tỷ lệ với tỷ lệ của thời kỳ tương ứng và số năm trên tổng số lần thanh toánkỳ:
- Đối với đối số rate , hãy chia lãi suất hàng năm cho số lần thanh toán mỗi năm, giả sử số lần thanh toán sau bằng với số kỳ gộp mỗi năm.
- Đối với đối số nper , hãy nhân số năm với số lần thanh toán mỗi năm.
Bảng sau hiển thị các phép tính:
| Tần suất thanh toán | Đối số tỷ lệ | Đối số Nper |
| Hàng tuần | lãi hàng năm lãi suất / 52 | năm * 52 |
| Lãi suất hàng tháng | hàng năm / 12 | năm * 12 |
| Hàng quý | lãi suất hàng năm / 4 | năm * 4 |
| Nửa năm | hàng năm lãi suất / 2 | năm * 2 |
Ví dụ: hãy tìm số tiền lãi bạn sẽ phải trả cho cùng một khoản vay nhưng ở các thời điểm khác nhau tần suất thanh toán:
- Lãi suất hàng năm: 6%
- Thời hạn cho vay: 2 năm
- Số tiền cho vay: 20.000 USD
- Thời hạn: 1
Số dư sau r khoản thanh toán cuối cùng là $0 (bỏ qua đối số fv ) và các khoản thanh toán đến hạn vào cuối mỗi kỳ (bỏ qua đối số type ).
Hàng tuần :
=IPMT(6%/52, 1, 2*52, 20000)
Hàng tháng :
=IPMT(6%/12, 1, 2*12, 20000)
Hàng quý :
=IPMT(6%/4, 1, 2*4, 20000)
Nửa năm một lần :
=IPMT(6%/2, 1, 2*2, 20000)
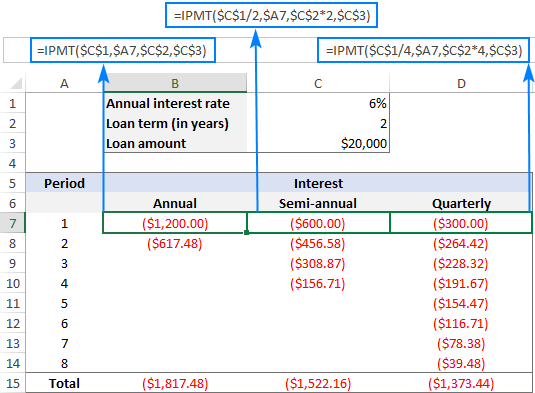
Nhìn vào ảnh chụp màn hình bên dưới, bạn có thể nhận thấy rằng số tiền lãi giảm dần theo từng thời kỳ tiếp theo. Đây làbởi vì bất kỳ khoản thanh toán nào cũng góp phần làm giảm số tiền gốc của khoản vay và điều này làm giảm số dư còn lại mà tiền lãi được tính.
Ngoài ra, xin lưu ý rằng tổng số tiền lãi phải trả cho cùng một khoản vay sẽ khác nhau giữa hàng năm và nửa năm và trả góp hàng quý:
Dạng đầy đủ của hàm IPMT
Trong ví dụ này, chúng ta sẽ tính lãi cho cùng một khoản vay, cùng tần suất thanh toán , nhưng các loại niên kim khác nhau (thông thường và niên kim đến hạn). Đối với điều này, chúng ta sẽ cần sử dụng dạng đầy đủ của hàm IPMT.
Để bắt đầu, hãy xác định các ô đầu vào:
- B1 - lãi suất hàng năm
- B2 - thời hạn cho vay tính theo năm
- B3 - số lần thanh toán mỗi năm
- B4 - số tiền cho vay ( pv )
- B5 - giá trị tương lai ( fv )
- B6 - khi đến hạn thanh toán ( type ):
- 0 - vào cuối kỳ (dòng niên kim thông thường)
- 1 - vào đầu kỳ (hưu kim đến hạn)
Giả sử số đầu kỳ là A9, công thức tính lãi của chúng tôi như sau:
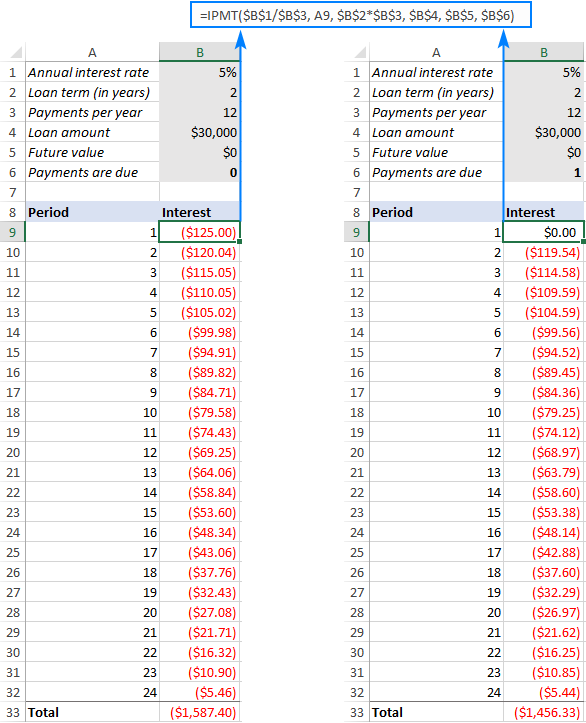
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
Lưu ý. Nếu bạn dự định sử dụng công thức IPMT trong hơn một khoảng thời gian, vui lòng lưu ý đến các tham chiếu ô. Tất cả các tham chiếu đến các ô đầu vào sẽ là tuyệt đối (có ký hiệu đô la) để chúng bị khóa đối với các ô đó. Đối số per phải là một tham chiếu ô tương đối (không có ký hiệu đô la như A9) vì nó sẽ thay đổi dựa trênvị trí tương đối của một hàng mà công thức được sao chép.
Vì vậy, chúng tôi nhập công thức trên vào B9, kéo nó xuống trong các khoảng thời gian còn lại và nhận được kết quả sau. Nếu bạn so sánh các số trong cột Lãi suất (dòng niên kim thông thường ở bên trái và niên kim đến hạn ở bên phải), bạn sẽ nhận thấy rằng tiền lãi thấp hơn một chút khi bạn thanh toán vào đầu kỳ.
Chức năng IPMT của Excel không hoạt động
Nếu công thức IPMT của bạn báo lỗi, rất có thể đó là một trong những nguyên nhân sau:
- #NUM! xảy ra lỗi là đối số per nằm ngoài phạm vi từ 1 đến nper .
- #VALUE! xảy ra lỗi nếu bất kỳ đối số nào không phải là số.
Đó là cách bạn sử dụng hàm IPMT trong Excel. Để xem kỹ hơn các công thức được thảo luận trong hướng dẫn này, bạn có thể tải xuống sổ làm việc mẫu hàm Excel IPMT của chúng tôi. Tôi cảm ơn bạn đã đọc và hy vọng sẽ gặp bạn trên blog của chúng tôi vào tuần tới!

