අන්තර්ගත වගුව
ණයක් හෝ උකසක් මත වාරික ගෙවීමක පොලී කොටස සොයා ගැනීමට Excel හි IPMT ශ්රිතය භාවිතා කරන ආකාරය නිබන්ධනය පෙන්වයි.
ඔබ ණයක් ගන්නා ඕනෑම අවස්ථාවක, එය උකසක්, නිවාස ණයක් හෝ මෝටර් රථ ණයක් වේවා, ඔබ මුලින් ණයට ගත් මුදල සහ ඊට උඩින් පොලිය ආපසු ගෙවිය යුතුය. සරලව කිවහොත්, පොලී යනු යමෙකුගේ (සාමාන්යයෙන් බැංකුවක) මුදල් භාවිතා කිරීමේ පිරිවැයයි.
ණය ගෙවීමක පොලී කොටස, කාල සීමාවේ පොලී අනුපාතය ඉතිරි ශේෂයෙන් ගුණ කිරීමෙන් අතින් ගණනය කළ හැක. නමුත් Microsoft Excel මේ සඳහා විශේෂ කාර්යයක් ඇත - IPMT ශ්රිතය. මෙම නිබන්ධනයේදී, අපි එහි වාක්ය ඛණ්ඩය විස්තර කරමින් සහ සැබෑ ජීවිත සූත්ර උදාහරණ සපයන්නෙමු.
Excel IPMT ශ්රිතය - වාක්ය ඛණ්ඩය සහ මූලික භාවිතයන්
IPMT යනු Excel හි පොලී ගෙවීමේ කාර්යයයි. එය ලබා දී ඇති කාල සීමාවක් තුළ ණය ගෙවීමක පොලී මුදල ආපසු ලබා දෙයි, පොලී අනුපාතිකය සහ ගෙවීමේ මුළු මුදල සියලු කාල පරිච්ඡේදවල නියත යැයි උපකල්පනය කරයි.
ශ්රිතයේ නම වඩා හොඳින් මතක තබා ගැනීමට, "I" යන්න සටහන් කර ගන්න. "පොලී" සඳහා සහ "ගෙවීම්" සඳහා "PMT".
Excel හි IPMT ශ්රිතයේ වාක්ය ඛණ්ඩය පහත පරිදි වේ:
IPMT(අනුපාතය, per, nper, pv, [fv], [type ])කොතැනද:
- අනුපාත (අවශ්යයි) - කාල සීමාවකට නියත පොලී අනුපාතය. ඔබට එය ප්රතිශතයක් හෝ දශම සංඛ්යාවක් ලෙස සැපයිය හැක.
උදාහරණයක් ලෙස, ඔබ වාර්ෂිකව ණයක් මත වාර්ෂික ගෙවීම් කරන්නේ නම්සියයට 6 ක පොලී අනුපාතයක්, අනුපාතය සඳහා 6% හෝ 0.06 භාවිතා කරන්න.
ඔබ සතිපතා, මාසිකව හෝ කාර්තුමය ගෙවීම් කරන්නේ නම්, වාර්ෂික ගාස්තුව වසරකට ගෙවීම් කාල ගණනින් බෙදන්න, මෙම උදාහරණයේ පෙන්වා ඇති පරිදි. ඔබ සියයට 6ක වාර්ෂික පොලී අනුපාතයක් සහිත ණයක් මත කාර්තුමය ගෙවීම් කරන්නේ නම්, අනුපාතය සඳහා 6%/4 භාවිතා කරන්න.
- Per (අවශ්යයි) - ඔබට පොලී ගණනය කිරීමට අවශ්ය කාලසීමාව. එය 1 සිට nper දක්වා පරාසයක පූර්ණ සංඛ්යාවක් විය යුතුය.
- Nper (අවශ්යයි) - ණයෙහි ජීවිත කාලය තුළ මුළු ගෙවීම් ගණන.
- Pv (අවශ්යයි) - ණයෙහි හෝ ආයෝජනයේ වර්තමාන වටිනාකම. වෙනත් වචන වලින් කිවහොත්, එය ණය මූලිකය, එනම් ඔබ ණයට ගත් මුදලයි.
- Fv (විකල්ප) - අනාගත අගය, එනම් අවසන් ගෙවීමෙන් පසු අපේක්ෂිත ශේෂය. ඉවත් කර ඇත්නම්, එය ශුන්ය (0) ලෙස ඇඟවුම් කෙරේ.
- වර්ගය (විකල්ප) - ගෙවීම් නියමිත වේලාව සඳහන් කරයි:
- 0 හෝ මඟ හැරිය - ගෙවීම් සිදු කෙරේ. එක් එක් කාල සීමාව අවසානයේ.
- 1 - එක් එක් කාලපරිච්ඡේදය ආරම්භයේදී ගෙවීම් කරනු ලැබේ.
උදාහරණයක් ලෙස, ඔබ ඩොලර් 20,000 ක ණයක් ලබා ගත්තේ නම් , 6% ක වාර්ෂික පොලී අනුපාතයක් සමඟින් ඉදිරි වසර 3 තුළ ඔබ වාර්ෂික වාරිකවලින් ගෙවිය යුතු, 1 වන වසරේ ගෙවීමේ පොලී කොටස මෙම සූත්රය සමඟ ගණනය කළ හැක:
=IPMT(6%, 1, 3, 20000)
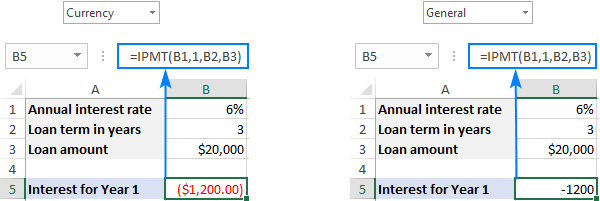
සංඛ්යා සෘජුවම සූත්රයකට සැපයීම වෙනුවට, ඔබට හැකියඒවා සමහර පූර්ව නිශ්චිත කොටු තුළට ඇතුළු කර පහත තිර රුවෙහි පෙන්වා ඇති පරිදි එම සෛල වෙත යොමු වන්න.
මුදල් ප්රවාහ ලකුණ සම්මුතියට අනුව, ඔබ ගෙවන නිසා ප්රතිඵලය සෘණ අංකයක් ලෙස ලබාදේ මෙම මුදල් වලින්. පෙරනිමියෙන්, එය රතු පැහැයෙන් උද්දීපනය කර ඇති අතර පහත තිර පිටුවේ වම් කොටසේ පෙන්වා ඇති පරිදි වරහන් තුළ ( මුදල් සෘණ අංක සඳහා ආකෘතිය) කොටා ඇත. දකුණු පසින්, ඔබට සාමාන්ය ආකෘතියෙන් එකම සූත්රයේ ප්රතිඵල දැකිය හැක.
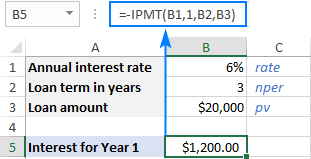
ඔබ කැමති නම් <8 ලෙස>ධන අංකය , සම්පූර්ණ IPMT ශ්රිතයට හෝ pv තර්කයට පෙර අඩු ලකුණක් දමන්න:
=-IPMT(6%, 1, 3, 20000)
හෝ
=IPMT(6%, 1, 3, -20000)
Excel හි IPMT සූත්රය භාවිතා කිරීමේ උදාහරණ
දැන් ඔබ මූලික කරුණු දන්නා නිසා, විවිධ සඳහා පොලී ප්රමාණය සොයා ගැනීමට IPMT ශ්රිතය භාවිතා කරන්නේ කෙසේදැයි බලමු. ගෙවීමේ සංඛ්යාත, සහ ණය කොන්දේසි වෙනස් කිරීම විභව පොලී වෙනස් කරන ආකාරය.
අපි කිමිදීමට පෙර, ආවර්තිතා කාලයක මුළු මුදල ගණනය කරන PMT ශ්රිතයෙන් පසුව IPMT සූත්ර භාවිතා කිරීම වඩාත් සුදුසු බව සටහන් කළ යුතුය. ගෙවීම (පොලී + මූලික).
විවිධ ගෙවීම් සංඛ්යාත සඳහා IPMT සූත්රය (සති, මාස, කාර්තු)
ණය ගෙවීමක පොලී කොටස නිවැරදිව ලබා ගැනීමට, ඔබ සැම විටම වාර්ෂික පොලිය පරිවර්තනය කළ යුතුය අනුරූප කාලපරිච්ඡේදයේ අනුපාතයට අනුපාතය සහ මුළු ගෙවීම් ගණනට වසර ගණනකාලපරිච්ඡේද:
- අනුපාත තර්කය සඳහා, වාර්ෂික පොලී අනුපාතිකය වසරකට ගෙවීම් සංඛ්යාවෙන් බෙදන්න, දෙවැන්න වසරකට සංයෝජන කාල ගණනට සමාන යැයි උපකල්පනය කරන්න.
- nper තර්කය සඳහා, වසර ගණන වසරකට ගෙවීම් ගණනින් ගුණ කරන්න.
පහත වගුව ගණනය කිරීම් පෙන්වයි:
| ගෙවීමේ වාර ගණන | අනුපාත තර්කය | Nper තර්කය |
| සතිපතා | වාර්ෂික පොලී අනුපාතය / 52 | වසර * 52 |
| මාසික | වාර්ෂික පොලී අනුපාතය / 12 | වසර * 12 |
| කාර්තුමය | වාර්ෂික පොලී අනුපාතය / 4 | වසර * 4 |
| අර්ධ වාර්ෂික | වාර්ෂික පොලී අනුපාතය / 2 | වසර * 2 |
උදාහරණයක් ලෙස, ඔබ එකම ණය සඳහා ගෙවිය යුතු පොලී ප්රමාණය සොයා බලමු. ගෙවීම් සංඛ්යාත:
- වාර්ෂික පොලී අනුපාතය: 6%
- ණය කාලය: අවුරුදු 2
- ණය මුදල: $20,000
- කාලසීමාව: 1<11
පසු ශේෂය r අවසාන ගෙවීම $0 විය යුතුය ( fv තර්කය ඉවත් කර ඇත), සහ ගෙවීම් එක් එක් කාල සීමාව අවසානයේ දී ගෙවිය යුතුය ( වර්ගය තර්කය ඉවත් කර ඇත).
සතිපතා :
=IPMT(6%/52, 1, 2*52, 20000)
මාසික :
=IPMT(6%/12, 1, 2*12, 20000)
කාර්තුමය :
=IPMT(6%/4, 1, 2*4, 20000)
අර්ධ වාර්ෂික :
=IPMT(6%/2, 1, 2*2, 20000)
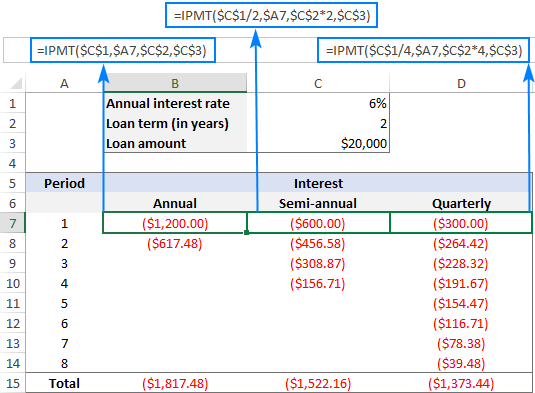
පහත තිර රුව දෙස බලන විට, පොලී මුදල බව ඔබට පෙනී යා හැක. එක් එක් ඊළඟ කාල පරිච්ඡේදය සමඟ අඩු වේ. මෙයමක්නිසාද යත් ඕනෑම ගෙවීමක් ණය ප්රධානය අඩු කිරීමට දායක වන අතර, මෙය පොලී ගණනය කරන ඉතිරි ශේෂය අඩු කරයි.
එමෙන්ම, එම ණය සඳහා ගෙවිය යුතු මුළු පොලී ප්රමාණය වාර්ෂික, අර්ධ වාර්ෂික සඳහා වෙනස් වන බව කරුණාවෙන් සලකන්න. සහ ත්රෛමාසික වාරික:
IPMT ශ්රිතයේ සම්පූර්ණ ස්වරූපය
මෙම උදාහරණයේ දී, අපි එම ණය සඳහාම පොලී ගණනය කරන්නෙමු, එකම ගෙවීම් සංඛ්යාතය , නමුත් විවිධ වාර්ෂික වර්ග (සාමාන්ය සහ වාර්ෂික වාරිකය). මේ සඳහා, අපට IPMT ශ්රිතයේ සම්පූර්ණ ස්වරූපය භාවිතා කිරීමට අවශ්ය වනු ඇත.
ආරම්භ කිරීමට, අපි ආදාන කොටු නිර්වචනය කරමු:
- B1 - වාර්ෂික පොලී අනුපාතය 10>B2 - වසරවල ණය වාරය
- B3 - වසරකට ගෙවීම් ගණන
- B4 - ණය මුදල ( pv )
- B5 - අනාගත අගය ( fv )
- B6 - ගෙවීම් නියමිත විට ( වර්ගය ):
- 0 - කාල සීමාවක් අවසානයේ (සාමාන්ය වාර්ෂික)
- 1 - කාලපරිච්ඡේදයක ආරම්භයේදී (වාර්ෂිකව ගෙවිය යුතු)
පළමු කාල පරිච්ඡේද අංකය A9 හි ඇතැයි උපකල්පනය කළහොත්, අපගේ පොලී සූත්රය පහත පරිදි වේ:
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
සටහන. ඔබ එක් කාල පරිච්ඡේදයකට වඩා IPMT සූත්රය භාවිතා කිරීමට අදහස් කරන්නේ නම්, කරුණාකර සෛල යොමු මතක තබා ගන්න. ආදාන සෛල සඳහා වන සියලුම යොමු කිරීම් නිරපේක්ෂ විය යුතුය (ඩොලර් ලකුණ සමඟ) එබැවින් ඒවා එම සෛලවලට අගුලු දමා ඇත. per තර්කය සාපේක්ෂ සෛල යොමුවක් විය යුතුය (A9 වැනි ඩොලර් ලකුණ නොමැතිව) එය වෙනස් විය යුත්තේසූත්රය පිටපත් කර ඇති පේළියක සාපේක්ෂ පිහිටීම.
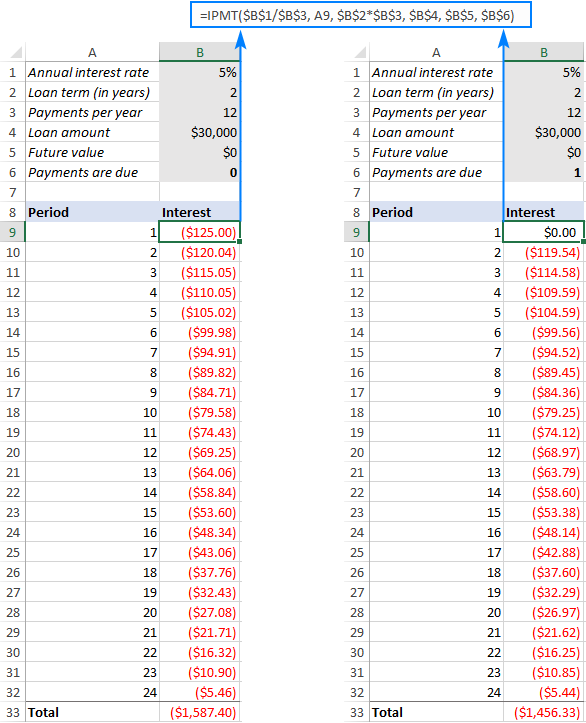
ඉතින්, අපි ඉහත සූත්රය B9 හි ඇතුළත් කර, ඉතිරි කාල පරිච්ඡේද සඳහා එය පහළට ඇදගෙන පහත ප්රතිඵලය ලබා ගනිමු. ඔබ පොළිය තීරුවල ඇති සංඛ්යා සංසන්දනය කළහොත් (වමේ නිත්ය වාර්ෂික වාරිකය සහ දකුණේ වාර්ෂික වාරිකය), ඔබ කාලසීමාව ආරම්භයේදී ගෙවන විට පොලී ටිකක් අඩු බව ඔබට පෙනී යනු ඇත.
Excel IPMT ශ්රිතය ක්රියා නොකරයි
ඔබගේ IPMT සූත්රය දෝෂයක් ඇති කරයි නම්, එය බොහෝ විට පහත ඒවායින් එකක් වීමට ඉඩ ඇත:
- #NUM! දෝශයක් හටගන්නේ per තර්කය 1 සිට nper දක්වා පරාසයෙන් පිටතය.
- #VALUE! කිසියම් තර්කයක් සංඛ්යාත්මක නොවන නම් දෝෂයක් ඇතිවේ.
ඔබ Excel හි IPMT ශ්රිතය භාවිතා කරන්නේ එලෙසයි. මෙම නිබන්ධනයේ සාකච්ඡා කර ඇති සූත්ර දෙස සමීපව බැලීමට, අපගේ Excel IPMT ක්රියාකාරී නියැදි වැඩපොත බාගත කිරීමට ඔබව සාදරයෙන් පිළිගනිමු. කියවීම ගැන මම ඔබට ස්තූතිවන්ත වන අතර ලබන සතියේ අපගේ බ්ලොග් අඩවියෙන් ඔබව දැකීමට බලාපොරොත්තු වෙමි!

