Indholdsfortegnelse
Vejledningen viser, hvordan du bruger IPMT-funktionen i Excel til at finde rentedelen af en periodisk betaling på et lån eller et realkreditlån.
Når du optager et lån, uanset om det er et realkreditlån, et boliglån eller et billån, skal du betale det beløb, du oprindeligt lånte, tilbage og renter oveni. Renter er ganske enkelt prisen for at bruge andres (som regel en banks) penge.
Rentedelen af en lånebetaling kan beregnes manuelt ved at gange periodens rentesats med den resterende saldo. Men Microsoft Excel har en særlig funktion til dette - IPMT-funktionen. I denne vejledning vil vi gå i dybden med at forklare dens syntaks og give eksempler på formler fra det virkelige liv.
Excel IPMT-funktion - syntaks og grundlæggende anvendelser
IPMT er Excels rentebetalingsfunktion. Den returnerer rentebeløbet for en lånebetaling i en given periode, idet det antages, at rentesatsen og det samlede beløb for en betaling er konstant i alle perioder.
For at du bedre kan huske funktionens navn, skal du bemærke, at "I" står for "rente" og "PMT" for "betaling".
Syntaksen for IPMT-funktionen i Excel er som følger:
IPMT(rate, per, nper, pv, [fv], [type])Hvor:
- Vurder (påkrævet) - den konstante rentesats pr. periode. Du kan angive den som en procentdel eller et decimaltal.
Hvis du f.eks. laver årlige betalinger på et lån med en årlig rente på 6 procent, skal du bruge 6 % eller 0,06 for sats .
Hvis du foretager ugentlige, månedlige eller kvartalsvise betalinger, skal du dividere den årlige sats med antallet af betalingsperioder pr. år, som vist i dette eksempel. Hvis du f.eks. foretager kvartalsvis betalinger på et lån med en årlig rente på 6 procent, skal du bruge 6%/4 for sats .
- Pr. (påkrævet) - den periode, som renten skal beregnes for. Det skal være et helt tal i intervallet 1 til nper .
- Nper (påkrævet) - det samlede antal betalinger i løbet af lånets løbetid.
- Pv (påkrævet) - nutidsværdien af lånet eller investeringen. Med andre ord er det lånets hovedstol, dvs. det beløb, du har lånt.
- Fv (valgfrit) - den fremtidige værdi, dvs. den ønskede saldo efter den sidste betaling. Hvis den udelades, er den underforstået nul (0).
- Type (valgfrit) - angiver, hvornår betalingerne skal forfalde:
- 0 eller udeladt - betalingerne foretages ved udgangen af hver periode.
- 1 - betalinger foretages i begyndelsen af hver periode.
Hvis du f.eks. har modtaget et lån på 20.000 dollars, som du skal betale tilbage i årlige afdrag i de næste 3 år med en årlig rente på 6 %, kan rentedelen af det første års betaling beregnes med denne formel:
=IPMT(6%, 1, 3, 20000)
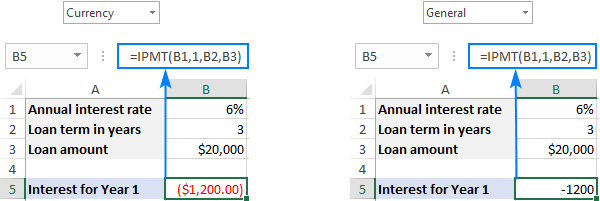
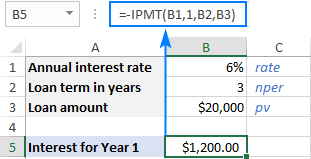
I stedet for at indtaste tallene direkte i en formel kan du indtaste dem i nogle foruddefinerede celler og henvise til disse celler som vist i skærmbilledet nedenfor.
I overensstemmelse med konventionen om pengestrømstegn returneres resultatet som en negativ nummer, fordi du udbetaler disse penge. Som standard er det markeret med rødt og omgivet af parenteser ( Valuta format for negative tal), som vist i den venstre del af skærmbilledet nedenfor. Til højre kan du se resultatet af den samme formel i Generelt format.
Hvis du hellere vil have renter som en positivt tal , sætte et minustegn foran enten hele IPMT-funktionen eller pv argument:
=-IPMT(6%, 1, 3, 20000)
eller
=IPMT(6%, 1, 3, -20000)
Eksempler på brug af IPMT-formlen i Excel
Nu hvor du kender det grundlæggende, skal vi se, hvordan du kan bruge IPMT-funktionen til at finde rentebeløbet for forskellige betalingshyppigheder, og hvordan ændrede lånebetingelser ændrer den potentielle rente.
Før vi går i dybden, skal det bemærkes, at IPMT-formler bedst anvendes efter PMT-funktionen, der beregner det samlede beløb for en periodisk betaling (renter + hovedstol).
IPMT-formel for forskellige betalingshyppigheder (uger, måneder, kvartaler)
For at få den rigtige rentedel af en lånebetaling skal du altid omregne den årlige rente til den tilsvarende periodes rente og antallet af år til det samlede antal betalingsperioder:
- For den sats argumentet, divideres den årlige rente med antallet af betalinger pr. år, idet det antages, at sidstnævnte er lig med antallet af rentes renteperioder pr. år.
- For den nper argument , multiplicer antallet af år med antallet af betalinger pr. år.
Følgende tabel viser beregningerne:
| Betalingshyppighed | Satsargument | Nper argument |
| Ugentlig | årlig rentesats / 52 | år * 52 |
| Månedlig | årlig rentesats / 12 | år * 12 |
| Kvartalsvis | årlig rentesats / 4 | år * 4 |
| Halvårligt | årlig rentesats / 2 | år * 2 |
Lad os som eksempel finde det rentebeløb, du skal betale for det samme lån, men med forskellige betalingshyppigheder:
- Årlig rentesats: 6 %.
- Lånets løbetid: 2 år
- Lånebeløb: 20.000 USD
- Periode: 1
Saldoen efter den sidste betaling skal være 0 USD (den fv argument udeladt), og betalingerne forfalder ved udgangen af hver periode (den type argument udeladt).
Ugentlig :
=IPMT(6%/52, 1, 2*52, 20000)
Månedlig :
=IPMT(6%/12, 1, 2*12, 20000)
Kvartalsvis :
=IPMT(6%/4, 1, 2*4, 20000)
Halvårligt :
=IPMT(6%/2, 1, 2*2, 20000)
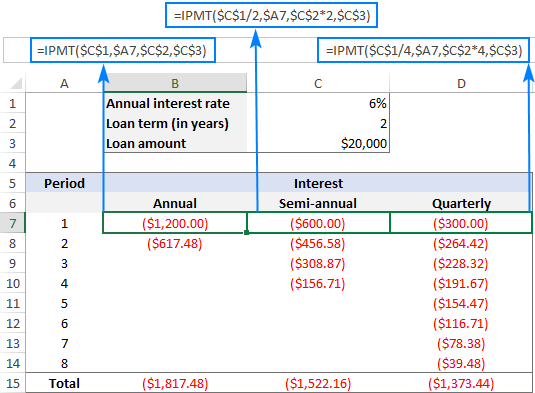
Hvis du ser på skærmbilledet nedenfor, kan du se, at rentebeløbet falder med hver efterfølgende periode. Det skyldes, at enhver betaling bidrager til at reducere lånets hovedstol, og det reducerer den resterende saldo, som renterne beregnes på.
Bemærk også, at det samlede rentebeløb, der skal betales for det samme lån, er forskelligt for årlige, halvårlige og kvartalsvise afdrag:
Den fulde form af IPMT-funktionen
I dette eksempel skal vi beregne renter for det samme lån, den samme betalingshyppighed, men forskellige annuitetsformer (almindelig og forfaldne annuiteter). Til dette formål skal vi bruge den fulde form af IPMT-funktionen.
Lad os til at begynde med definere indgangscellerne:
- B1 - årlig rentesats
- B2 - lånets løbetid i år
- B3 - antal betalinger pr. år
- B4 - lånebeløb ( pv )
- B5 - fremtidig værdi ( fv )
- B6 - hvornår betalingerne forfalder ( type ):
- 0 - ved udgangen af en periode (almindelig annuitetsrente)
- 1 - ved periodens begyndelse (forfalden annuitetsrente)
Hvis vi antager, at det første periodetal er i A9, lyder vores renteformel således:
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
Bemærk: Hvis du planlægger at bruge IPMT-formlen til mere end én periode, skal du være opmærksom på cellehenvisningerne. Alle henvisninger til inputcellerne skal være absolutte (med dollartegn), så de er låst til disse celler. pr. argumentet skal være en relativ cellehenvisning (uden dollartegn som A9), fordi det skal ændres afhængigt af den relative position i den række, som formlen kopieres til.
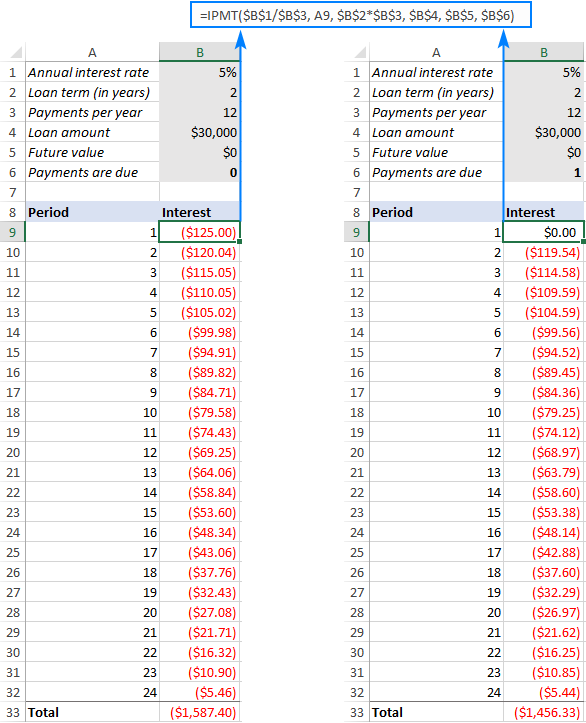
Så vi indtaster ovenstående formel i B9, trækker den ned for de resterende perioder og får følgende resultat. Hvis du sammenligner tallene i Renter kolonner (almindelig annuitetsrente til venstre og forfaldne annuitetsrente til højre), vil du bemærke, at renten er lidt lavere, når du betaler i begyndelsen af perioden.
Excel IPMT-funktionen virker ikke
Hvis din IPMT-formel giver anledning til en fejl, er det sandsynligvis en af følgende fejl:
- #NUM! fejl opstår er den pr. argumentet er uden for intervallet 1 til nper .
- #VALUE! opstår en fejl, hvis et af argumenterne er ikke-numerisk.
Sådan bruger du IPMT-funktionen i Excel. Hvis du vil se nærmere på de formler, der er beskrevet i denne vejledning, er du velkommen til at downloade vores Excel-arbejdsbog med eksempler på IPMT-funktionen. Tak for din læsning og håber at se dig på vores blog i næste uge!

