বিষয়বস্তুৰ তালিকা
টিউটোৰিয়েলত দেখুওৱা হৈছে যে ঋণ বা বন্ধকীৰ ওপৰত সময়ে সময়ে দিয়া ধনৰ সুতৰ অংশ বিচাৰি উলিয়াবলৈ এক্সেলত IPMT ফাংচন কেনেকৈ ব্যৱহাৰ কৰিব পাৰি।
যেতিয়াই আপুনি ঋণ লয়, সেয়া বন্ধকী হওক, ঘৰ ঋণ হওক বা গাড়ীৰ ঋণ হওক, আপুনি প্ৰথমে ঋণ লোৱা ধন আৰু তাৰ ওপৰত সুত ঘূৰাই দিব লাগিব। সহজ ভাষাত ক’বলৈ গ’লে সুত হ’ল কাৰোবাৰ (সাধাৰণতে বেংকৰ) ধন ব্যৱহাৰ কৰাৰ খৰচ।
ঋণ পৰিশোধৰ সুতৰ অংশটো সময়ছোৱাৰ সুতৰ হাৰক বাকী থকা বেলেঞ্চৰ সৈতে গুণ কৰি হাতেৰে গণনা কৰিব পাৰি। কিন্তু ইয়াৰ বাবে মাইক্ৰ’ছফ্ট এক্সেলৰ এটা বিশেষ ফাংচন আছে - আইপিএমটি ফাংচন। এই টিউটোৰিয়েলত আমি ইয়াৰ বাক্যবিন্যাসৰ বিষয়ে গভীৰভাৱে ব্যাখ্যা কৰিম আৰু বাস্তৱ জীৱনৰ সূত্ৰৰ উদাহৰণ দিম।
Excel IPMT ফাংচন - বাক্যবিন্যাস আৰু মৌলিক ব্যৱহাৰসমূহ
IPMT হৈছে এক্সেলৰ সুত পৰিশোধৰ কাৰ্য্য। ই এটা নিৰ্দিষ্ট সময়ছোৱাত ঋণ পৰিশোধৰ সুতৰ পৰিমাণ ঘূৰাই দিয়ে, সুতৰ হাৰ আৰু পৰিশোধৰ মুঠ পৰিমাণ সকলো সময়ছোৱাত স্থিৰ বুলি ধৰি লৈ।
ফাংচনটোৰ নামটো ভালদৰে মনত ৰাখিবলৈ, মন কৰক যে "I" থিয় হৈ আছে "সুদ"ৰ বাবে আৰু "পেমেণ্ট"ৰ বাবে "PMT"।
এক্সেলত IPMT ফাংচনৰ বাক্যবিন্যাস নিম্নলিখিত:
IPMT(rate, per, nper, pv, [fv], [type ])ক'ত:
- হাৰ (প্ৰয়োজনীয়) - প্ৰতিটো সময়ছোৱাৰ স্থিৰ সুতৰ হাৰ। আপুনি ইয়াক শতাংশ বা দশমিক সংখ্যা হিচাপে যোগান ধৰিব পাৰে।
উদাহৰণস্বৰূপে, যদি আপুনি বাৰ্ষিক ঋণৰ সৈতে বাৰ্ষিক ধন পৰিশোধ কৰে৬ শতাংশ সুতৰ হাৰ, হাৰ ৰ বাবে ৬% বা ০.০৬ ব্যৱহাৰ কৰক।
যদি আপুনি সাপ্তাহিক, মাহেকীয়া বা ত্ৰিমাসিক পেমেণ্ট কৰে, তেন্তে বাৰ্ষিক হাৰক প্ৰতি বছৰে পেমেণ্টৰ সময়ৰ সংখ্যাৰে ভাগ কৰক, এই উদাহৰণত দেখুওৱাৰ দৰে। ধৰক, যদি আপুনি ৬ শতাংশ বাৰ্ষিক সুতৰ হাৰৰ ঋণত <৮>ত্ৰিমাসিক ধন পৰিশোধ কৰে, তেন্তে <১>হাৰ ৰ বাবে ৬%/৪ ব্যৱহাৰ কৰক।
- Per (প্ৰয়োজনীয়) - যিটো সময়ছোৱাৰ বাবে আপুনি সুত গণনা কৰিব বিচাৰে। ই 1 ৰ পৰা nper লৈকে এটা পূৰ্ণসংখ্যা হ'ব লাগিব।
- Nper (প্ৰয়োজনীয়) - ঋণৰ জীৱনকালত কৰা মুঠ ধন পৰিশোধৰ সংখ্যা।
- Pv (প্ৰয়োজনীয়) - ঋণ বা বিনিয়োগৰ বৰ্তমান মূল্য। অৰ্থাৎ ই ঋণৰ মূলধন অৰ্থাৎ আপুনি ঋণ লোৱা ধনৰাশি।
- Fv (ঐচ্ছিক) - ভৱিষ্যতৰ মূল্য অৰ্থাৎ শেষৰ ধন পৰিশোধ কৰাৰ পিছত আকাংক্ষিত বেলেঞ্চ। যদি বাদ দিয়া হয়, তেন্তে ইয়াক শূন্য (0) বুলি কোৱা হয়।
- ধৰণ (ঐচ্ছিক) - পেমেণ্ট কেতিয়া দিব লাগে ধাৰ্য্য কৰে:
- 0 বা বাদ দিয়া হয় - পেমেণ্ট কৰা হয় প্ৰতিটো সময়ৰ শেষত।
- 1 - প্ৰতিটো সময়ৰ আৰম্ভণিতে ধন পৰিশোধ কৰা হয়।
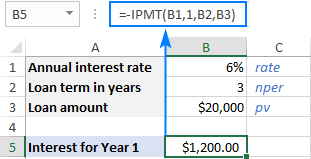
উদাহৰণস্বৰূপে, যদি আপুনি $20,000 ঋণ লাভ কৰে , যিটো আপুনি অহা ৩ বছৰৰ ভিতৰত বাৰ্ষিক কিস্তিত ৬% বাৰ্ষিক সুতৰ হাৰে পৰিশোধ কৰিব লাগিব, ১ম বছৰৰ পৰিশোধৰ সুতৰ অংশ এই সূত্ৰৰে গণনা কৰিব পাৰি:
=IPMT(6%, 1, 3, 20000)
সংখ্যাবোৰ পোনপটীয়াকৈ এটা সূত্ৰত যোগান ধৰাৰ পৰিৱৰ্তে, আপুনি পাৰেকিছুমান পূৰ্বনিৰ্ধাৰিত কোষত সিহতক ইনপুট কৰক আৰু তলৰ স্ক্ৰীণশ্বটত দেখুওৱাৰ দৰে সেই কোষসমূহ চাওক।
নগদ ধনৰ প্ৰবাহ চিহ্ন নিয়ম অনুসৰি, ফলাফলটো এটা ঋণাত্মক সংখ্যা হিচাপে ঘূৰাই দিয়া হয় কাৰণ আপুনি ধন দিয়ে এই ধন উলিয়াই। অবিকল্পিতভাৱে, ইয়াক ৰঙা ৰঙেৰে হাইলাইট কৰা হয় আৰু বন্ধনীত আবদ্ধ কৰা হয় (ঋণাত্মক সংখ্যাৰ বাবে মুদ্ৰা বিন্যাস) তলৰ পৰ্দাশটৰ বাওঁ অংশত দেখুওৱাৰ দৰে। সোঁফালে, আপুনি একেটা সূত্ৰৰ ফলাফল সাধাৰণ বিন্যাসত চাব পাৰে।
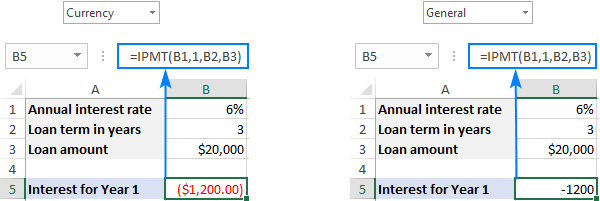
যদি আপুনি <8 হিচাপে আগ্ৰহ লাভ কৰাটো পছন্দ কৰে>ধনাত্মক সংখ্যা , সম্পূৰ্ণ IPMT ফাংচন বা pv যুক্তিৰ আগত এটা বিয়োগ চিহ্ন ৰাখক:
=-IPMT(6%, 1, 3, 20000)
বা
=IPMT(6%, 1, 3, -20000)
এক্সেলত IPMT সূত্ৰ ব্যৱহাৰ কৰাৰ উদাহৰণ
এতিয়া যেতিয়া আপুনি মূল কথাবোৰ জানে, চাওঁ আহক বিভিন্ন ৰ বাবে আগ্ৰহৰ পৰিমাণ বিচাৰিবলৈ IPMT ফাংচনটো কেনেকৈ ব্যৱহাৰ কৰিব পাৰি ঋণৰ চৰ্ত সলনি কৰিলে সম্ভাৱ্য সুত কেনেকৈ সলনি হয়।
আমি ডুব যোৱাৰ আগতে মন কৰিবলগীয়া যে আইপিএমটি সূত্ৰসমূহ পিএমটি ফাংচনৰ পিছত ব্যৱহাৰ কৰাটোৱেই উত্তম যিয়ে এটা সময়কালীন মুঠ পৰিমাণ গণনা কৰে পেমেন্ট (সুত + মূলধন)।
বিভিন্ন পেমেণ্ট ফ্ৰিকুৱেন্সিৰ বাবে আইপিএমটি সূত্ৰ (সপ্তাহ, মাহ, ত্ৰিমাসিক)
ঋণ পৰিশোধৰ অধিকাৰৰ সুতৰ অংশ পাবলৈ, আপুনি সদায় বাৰ্ষিক সুত ৰূপান্তৰ কৰিব লাগে হাৰক সংশ্লিষ্ট সময়ৰ হাৰলৈ আৰু বছৰৰ সংখ্যাৰ পৰা মুঠ পেমেণ্টৰ সংখ্যালৈসময়সীমা:
- হাৰ যুক্তিৰ বাবে, বাৰ্ষিক সুতৰ হাৰক প্ৰতি বছৰে দিয়া ধনৰ সংখ্যাৰে ভাগ কৰক, ধৰি লওক যে পিছৰটো প্ৰতি বছৰে কম্পাউণ্ডিং পিৰিয়ডৰ সংখ্যাৰ সমান।
- nper যুক্তি ৰ বাবে, বছৰৰ সংখ্যাক প্ৰতি বছৰে পেমেণ্টৰ সংখ্যাৰে গুণ কৰক।
তলৰ তালিকাখনে গণনাসমূহ দেখুৱাইছে:
| পেমেণ্টৰ কম্পাঙ্ক | হাৰ যুক্তি | এনপ্ৰতি যুক্তি |
| সাপ্তাহিক | বাৰ্ষিক সুত হাৰ / ৫২<১৯><১৮>বছৰ * ৫২<১৯><২০><১৭><১৮>মাহেকীয়া<১৯><১৮>বাৰ্ষিক সুতৰ হাৰ / ১২<১৯><১৮>বছৰ * ১২<১৯><২০> | |
| ত্ৰিমাসিক | বাৰ্ষিক সুতৰ হাৰ / 4 | বছৰ * 4 |
| অৰ্ধবাৰ্ষিক | বাৰ্ষিক interest rate / 2 | years * 2 |
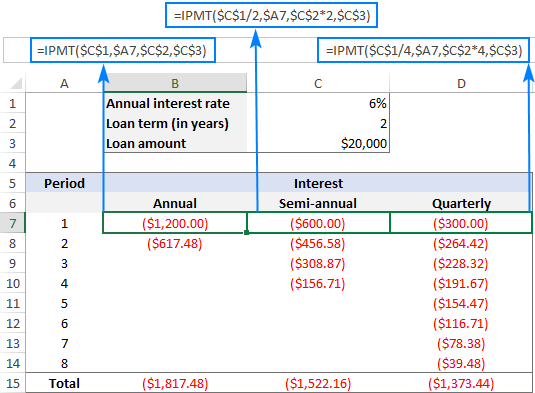
উদাহৰণস্বৰূপে একেটা ঋণৰ ওপৰত কিন্তু বেলেগ বেলেগ সুতৰ পৰিমাণ বিচাৰি উলিয়াওক ঋণৰ সময়সীমা: ২ বছৰ
ভাৰসাম্য afte r শেষৰ পেমেণ্ট $0 হ'ব লাগিব ( fv যুক্তি বাদ দিয়া হৈছে), আৰু পেমেণ্টসমূহ প্ৰতিটো সময়ৰ শেষত দিব লাগিব ( type যুক্তি বাদ দিয়া হৈছে)।
সাপ্তাহিক :
=IPMT(6%/52, 1, 2*52, 20000)
মাহেকীয়া :
=IPMT(6%/12, 1, 2*12, 20000)
ত্ৰিমাসিক :
=IPMT(6%/4, 1, 2*4, 20000)
ছেমি-বাৰ্ষিক :
=IPMT(6%/2, 1, 2*2, 20000)
তলৰ স্ক্ৰীণশ্বটটো চালে আপুনি লক্ষ্য কৰিব পাৰে যে সুতৰ পৰিমাণ পৰৱৰ্তী প্ৰতিটো সময়ৰ লগে লগে হ্ৰাস পায়। এইটোকাৰণ যিকোনো ধন পৰিশোধে ঋণৰ মূলধন হ্ৰাস কৰাত অৰিহণা যোগায়, আৰু ইয়াৰ ফলত বাকী থকা বেলেঞ্চ হ্ৰাস পায় যাৰ ওপৰত সুত গণনা কৰা হয়।
আৰু, অনুগ্ৰহ কৰি মন কৰক যে একেটা ঋণৰ ওপৰত প্ৰদান কৰিবলগীয়া মুঠ সুতৰ পৰিমাণ বাৰ্ষিক, অৰ্ধবাৰ্ষিকৰ বাবে পৃথক আৰু ত্ৰিমাসিক কিস্তি:
আইপিএমটি ফাংচনৰ সম্পূৰ্ণ ৰূপ
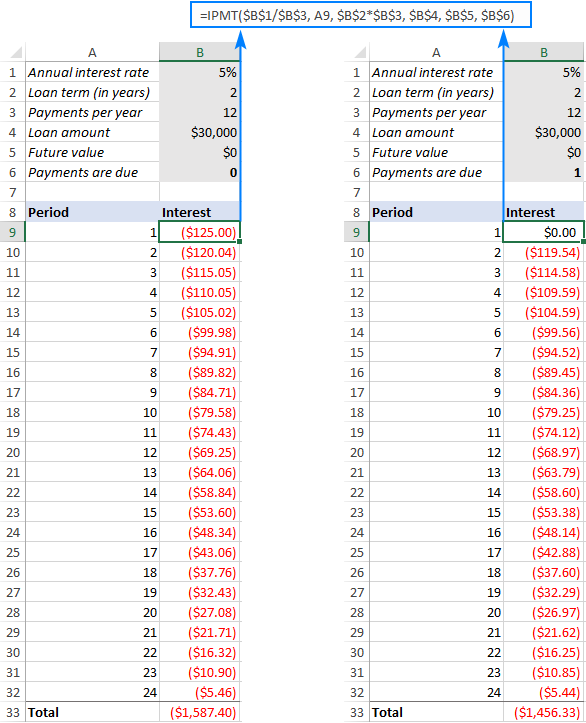
এই উদাহৰণত আমি একেটা ঋণৰ বাবে সুত গণনা কৰিবলৈ ওলাইছো, একেটা পেমেণ্ট ফ্ৰিকুৱেন্সি , কিন্তু বিভিন্ন বাৰ্ষিকী প্ৰকাৰৰ (নিয়মীয়া আৰু বাৰ্ষিকী-পাবলগীয়া)। ইয়াৰ বাবে আমি IPMT ফাংচনৰ সম্পূৰ্ণ ৰূপ ব্যৱহাৰ কৰিব লাগিব।
আৰম্ভণি কৰিবলৈ, ইনপুট কোষসমূহ সংজ্ঞায়িত কৰোঁ আহক:
- B1 - বাৰ্ষিক সুতৰ হাৰ <১০>B2 - বছৰত ঋণৰ সময়সীমা
- 0 - এটা সময়ৰ শেষত (নিয়মীয়া বাৰ্ষিকী)
- 1 - এটা পিৰিয়ডৰ আৰম্ভণিতে (বাৰ্ষিকী প্ৰাপ্য)
প্ৰথম পিৰিয়ড সংখ্যাটো A9 ত আছে বুলি ধৰি ল'লে আমাৰ সুতৰ সূত্ৰটো তলত দিয়া ধৰণে যায়:<৩><০>৯৪০৭<৩><০> টোকা। যদি আপুনি IPMT সূত্ৰটো এটাতকৈ অধিক সময়ৰ বাবে ব্যৱহাৰ কৰাৰ পৰিকল্পনা কৰিছে, অনুগ্ৰহ কৰি কোষৰ উল্লেখসমূহৰ প্ৰতি লক্ষ্য ৰাখক। ইনপুট কোষসমূহৰ সকলো উল্লেখ নিৰপেক্ষ হ'ব লাগিব (ডলাৰ চিহ্নৰ সৈতে) গতিকে সিহতক সেই কোষসমূহত লক কৰা হয়। per যুক্তিটো এটা আপেক্ষিক কোষ প্ৰসংগ হ'ব লাগিব (A9 ৰ দৰে ডলাৰ চিহ্ন অবিহনে) কাৰণ ই ৰ ওপৰত ভিত্তি কৰি সলনি হ'ব লাগেসূত্ৰটো কপি কৰা শাৰীৰ আপেক্ষিক অৱস্থান।
গতিকে, আমি ওপৰৰ সূত্ৰটো B9 ত সুমুৱাওঁ, বাকী থকা সময়ছোৱাৰ বাবে ইয়াক তললৈ টানি নিব, আৰু তলৰ ফলাফলটো পাম। যদি আপুনি সুত স্তম্ভত থকা সংখ্যাসমূহ তুলনা কৰে (বাওঁফালে নিয়মীয়া বাৰ্ষিকী আৰু সোঁফালে বাৰ্ষিকী-বাৰ্ষিকী), আপুনি লক্ষ্য কৰিব যে আপুনি সময়সীমাৰ আৰম্ভণিতে ধন পৰিশোধ কৰাৰ সময়ত সুত অলপ কম হয়।
Excel IPMT ফাংচনে কাম কৰা নাই
যদি আপোনাৰ IPMT সূত্ৰই এটা ভুল নিক্ষেপ কৰে, ই নিম্নলিখিতৰ এটা হোৱাৰ সম্ভাৱনা বেছি:
- <১০>#NUM! ত্ৰুটি ঘটে যদি per যুক্তিটো 1 ৰ পৰা nper লৈকে পৰিসীমাৰ বাহিৰত।
- #VALUE! ভুল হয় যদি কোনো যুক্তি অসংখ্যাগত হয়।
আপুনি Excel ত IPMT ফাংচনটো এনেদৰে ব্যৱহাৰ কৰে। এই টিউটোৰিয়েলত আলোচনা কৰা সূত্ৰসমূহ ভালদৰে চাবলৈ, আপুনি আমাৰ Excel IPMT ফাংচনৰ নমুনা কাৰ্য্যপুস্তিকা ডাউনলোড কৰিবলৈ আদৰণি জনোৱা হৈছে। পঢ়াৰ বাবে ধন্যবাদ আৰু অহা সপ্তাহত আমাৰ ব্লগত লগ পাম বুলি আশা কৰিলোঁ!

