Բովանդակություն
Ձեռնարկը ցույց է տալիս, թե ինչպես օգտագործել IPMT ֆունկցիան Excel-ում՝ վարկի կամ հիփոթեքի պարբերական վճարման տոկոսադրույքը գտնելու համար:
Ամեն անգամ, երբ դուք վարկ եք վերցնում, լինի դա հիփոթեքային, բնակարանային կամ մեքենայի վարկ, դուք պետք է վերադարձնեք սկզբնական փոխառված գումարը և տոկոսագումարը: Պարզ ասած, տոկոսները ինչ-որ մեկի (սովորաբար բանկի) փողերն օգտագործելու արժեքն են:
Վարկի վճարման տոկոսադրույքը կարելի է ձեռքով հաշվարկել՝ ժամանակաշրջանի տոկոսադրույքը բազմապատկելով մնացած մնացորդի վրա: Սակայն Microsoft Excel-ն ունի դրա համար հատուկ գործառույթ՝ IPMT ֆունկցիան: Այս ձեռնարկում մենք մանրամասն կբացատրենք դրա շարահյուսությունը և կներկայացնենք իրական բանաձևերի օրինակներ:
Excel IPMT ֆունկցիա - շարահյուսություն և հիմնական օգտագործում
IPMT Excel-ի տոկոսների վճարման գործառույթն է: Այն վերադարձնում է տվյալ ժամանակահատվածում վարկի վճարման տոկոսագումարը՝ ենթադրելով, որ տոկոսադրույքը և վճարման ընդհանուր գումարը հաստատուն են բոլոր ժամանակաշրջաններում:
Ֆունկցիայի անվանումը ավելի լավ հիշելու համար նշեք, որ «I» նշանակում է. «տոկոսների» համար և «PMT»՝ «վճարման»:
IPMT ֆունկցիայի շարահյուսությունը Excel-ում հետևյալն է.
IPMT(դրույքաչափ, մեկ, nper, pv, [fv], [տիպ ])Որտեղ.
- Դրույքաչափ (պարտադիր) - մշտական տոկոսադրույքը մեկ ժամանակաշրջանի համար: Դուք կարող եք այն տրամադրել որպես տոկոս կամ տասնորդական թիվ:
Օրինակ, եթե դուք տարեկան վճարումներ եք կատարում տարեկան վարկի համարտոկոսադրույքը 6 տոկոս, օգտագործեք 6% կամ 0,06 դրույքի համար:
Եթե շաբաթական, ամսական կամ եռամսյակային վճարումներ եք կատարում, տարեկան տոկոսադրույքը բաժանեք տարեկան վճարման ժամանակաշրջանների թվին, ինչպես ցույց է տրված այս օրինակում: Ասենք, եթե դուք եռամսյակային վճարումներ եք կատարում 6 տոկոս տարեկան տոկոսադրույքով վարկի համար, օգտագործեք 6%/4 դրույքի համար:
- Per (պարտադիր) - այն ժամանակահատվածը, որի համար ցանկանում եք հաշվարկել տոկոսները: Այն պետք է լինի 1-ից մինչև nper միջակայքում գտնվող ամբողջ թիվ:
- Nper (պարտադիր) - վարկի գործողության ընթացքում վճարումների ընդհանուր թիվը:
- Pv (պարտադիր) - վարկի կամ ներդրման ներկա արժեքը: Այլ կերպ ասած, դա վարկի մայր գումարն է, այսինքն՝ այն գումարը, որը դուք վերցրել եք։
- Fv (ըստ ցանկության)՝ ապագա արժեքը, այսինքն՝ ցանկալի մնացորդը վերջին վճարումից հետո։ Եթե բաց թողնված է, ապա ենթադրվում է, որ այն զրո է (0):
- Տեսակ (ըստ ցանկության) - նշում է, թե երբ են վճարումները կատարվում.
- 0 կամ բաց թողնված - վճարումները կատարվում են: յուրաքանչյուր ժամանակաշրջանի վերջում:
- 1 - վճարումները կատարվում են յուրաքանչյուր ժամանակաշրջանի սկզբում:
Օրինակ, եթե դուք ստացել եք $20,000 վարկ. , որը դուք պետք է մարեք տարեկան ապառիկներով առաջիկա 3 տարիների ընթացքում տարեկան 6% տոկոսադրույքով, 1-ին տարվա վճարման տոկոսադրույքը կարող է հաշվարկվել այս բանաձևով.
=IPMT(6%, 1, 3, 20000)
Թվերն ուղղակիորեն բանաձևի մեջ մտցնելու փոխարեն կարող եքմուտքագրեք դրանք որոշ նախապես սահմանված բջիջներում և հիշեք այդ բջիջները, ինչպես ցույց է տրված ստորև ներկայացված սքրինշոթում:
Համաձայն դրամական միջոցների հոսքերի նշանի կոնվենցիայի, արդյունքը վերադարձվում է որպես բացասական թիվ, քանի որ դուք վճարում եք: դուրս այս գումարը: Լռելյայնորեն այն ընդգծված է կարմիրով և փակագծերում ( Արժույթի ձևաչափ բացասական թվերի համար), ինչպես ցույց է տրված ստորև ներկայացված սքրինշոթի ձախ մասում: Աջ կողմում կարող եք տեսնել նույն բանաձևի արդյունքը Ընդհանուր ձևաչափով:
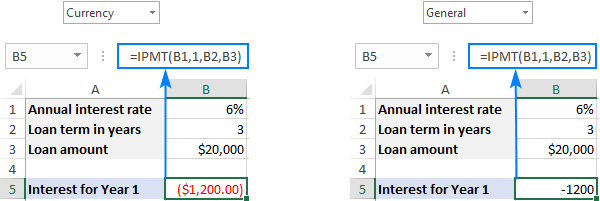
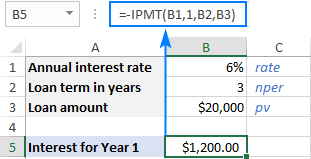
Եթե նախընտրում եք տոկոսներ ստանալ որպես դրական թիվ , դրեք մինուս նշան կամ ամբողջ IPMT ֆունկցիայի կամ pv արգումենտի առաջ՝
=-IPMT(6%, 1, 3, 20000)
կամ
=IPMT(6%, 1, 3, -20000)
Excel-ում IPMT բանաձևի օգտագործման օրինակներ
Այժմ, երբ դուք գիտեք հիմունքները, եկեք տեսնենք, թե ինչպես օգտագործել IPMT ֆունկցիան՝ տարբեր տոկոսների չափը գտնելու համար։ վճարման հաճախականությունը և ինչպես է փոխվում վարկի պայմանների փոփոխությունը պոտենցիալ տոկոսադրույքը:
Նախքան մեր մեջ մտնելը, հարկ է նշել, որ IPMT բանաձևերը լավագույնս օգտագործվում են PMT ֆունկցիայից հետո, որը հաշվարկում է պարբերականի ընդհանուր գումարը: վճարում (տոկոս + մայր գումար):
IPMT բանաձև տարբեր վճարումների հաճախականությունների համար (շաբաթներ, ամիսներ, եռամսյակներ)
Վարկի վճարման տոկոսադրույքը ճիշտ ստանալու համար միշտ պետք է փոխարկել տարեկան տոկոսադրույքը տոկոսադրույքը համապատասխան ժամանակաշրջանի դրույքաչափին և տարիների քանակը վճարումների ընդհանուր թվինժամանակաշրջաններ.
- դրույք փաստարկի համար տարեկան տոկոսադրույքը բաժանեք տարեկան վճարումների քանակի վրա՝ ենթադրելով, որ վերջինս հավասար է տարեկան բաղադրյալ ժամանակաշրջանների թվին:
- nper արգումենտի համար բազմապատկեք տարիների թիվը տարեկան վճարումների քանակով:
Հետևյալ աղյուսակը ցույց է տալիս հաշվարկները.
| Վճարման հաճախականությունը | Դրույքաչափի փաստարկ | Ան փաստարկ |
| Շաբաթական | տարեկան տոկոսադրույքը տոկոսադրույք / 52 | տարի * 52 |
| Ամսական | տարեկան տոկոսադրույք / 12 | տարի * 12 |
| Եռամսյակային | տարեկան տոկոսադրույք / 4 | տարի * 4 |
| Կիսամյակային | տարեկան տոկոսադրույք / 2 | տարի * 2 |
Որպես օրինակ, եկեք գտնենք տոկոսների չափը, որը դուք պետք է վճարեք նույն վարկի համար, բայց տարբեր վճարման հաճախականություններ՝
- Տարեկան տոկոսադրույք՝ 6%
- Վարկի տևողությունը՝ 2 տարի
- Վարկի գումարը՝ $20,000
- Ժամանակաշրջանը՝ 1
Մնացորդը հետո r վերջին վճարումը պետք է լինի $0 ( fv արգումենտը բաց է թողնվել), և վճարումները պետք է կատարվեն յուրաքանչյուր ժամանակաշրջանի վերջում ( type արգումենտը բաց է թողնվել):
Շաբաթական :
=IPMT(6%/52, 1, 2*52, 20000)
Ամսական :
=IPMT(6%/12, 1, 2*12, 20000)
Եռամսյակային :
=IPMT(6%/4, 1, 2*4, 20000)
Կիսամյակային :
=IPMT(6%/2, 1, 2*2, 20000)
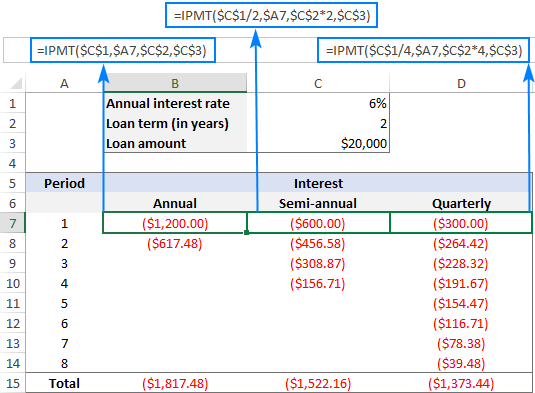
Նայելով ստորև ներկայացված սքրինշոթին, կարող եք նկատել, որ տոկոսագումարը նվազում է յուրաքանչյուր հաջորդ ժամանակահատվածի հետ: Սաքանի որ ցանկացած վճարում նպաստում է վարկի մայր գումարի կրճատմանը, և դա նվազեցնում է տոկոսների հաշվարկման մնացած մնացորդը:
Նաև, խնդրում ենք ուշադրություն դարձնել, որ նույն վարկի դիմաց վճարման ենթակա տոկոսների ընդհանուր գումարը տարբերվում է տարեկան, կիսամյակային կտրվածքով: և եռամսյակային վճարումներ՝
IPMT ֆունկցիայի ամբողջական ձևը
Այս օրինակում մենք հաշվարկելու ենք նույն վարկի տոկոսները, վճարման նույն հաճախականությունը , բայց տարբեր անուիտետների տեսակներ (կանոնավոր և անուիտետային ժամկետանց): Դրա համար մենք պետք է օգտագործենք IPMT ֆունկցիայի ամբողջական ձևը:
Սկզբից եկեք սահմանենք մուտքային բջիջները.
- B1 - տարեկան տոկոսադրույքը
- B2 - վարկի ժամկետը տարիներով
- B3 - տարեկան վճարումների քանակը
- B4 - վարկի գումարը ( pv )
- B5 - ապագա արժեքը ( fv )
- B6 - երբ վճարումները կատարվում են ( տեսակ ):
- 0 - ժամանակաշրջանի վերջում (կանոնավոր անուիտետ)
- 1 - ժամանակաշրջանի սկզբում (անուիտետի վճարում)
Ենթադրենք, որ առաջին ժամանակաշրջանի թիվը A9-ում է, մեր տոկոսադրույքի բանաձևը հետևյալն է. 3>
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
Ծանոթագրություն. Եթե նախատեսում եք օգտագործել IPMT բանաձևը մեկից ավելի ժամանակահատվածի համար, խնդրում ենք հաշվի առնել բջջային հղումները: Մուտքային բջիջների բոլոր հղումները պետք է լինեն բացարձակ (դոլարի նշանով), այնպես որ դրանք կողպված են այդ բջիջների վրա: per արգումենտը պետք է լինի հարաբերական բջջային հղում (առանց դոլարի նշանի, ինչպիսին A9-ն է), քանի որ այն պետք է փոխվի՝ հիմնվելովԱյն տողի հարաբերական դիրքը, որին պատճենված է բանաձևը:
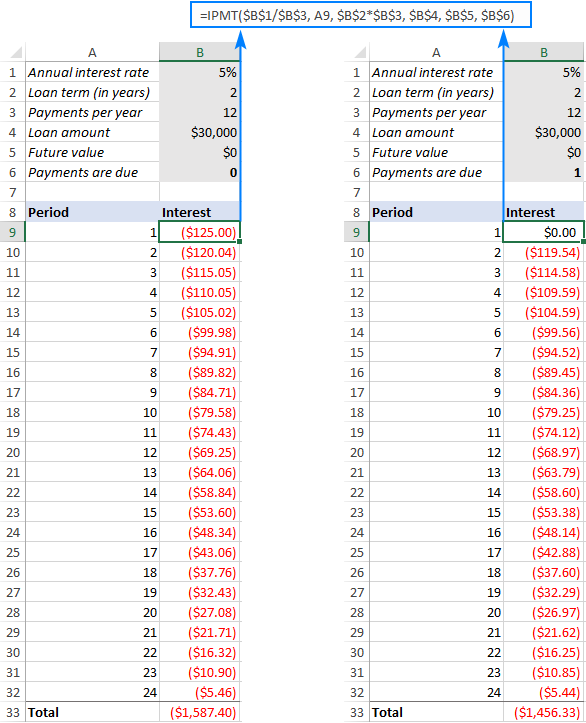
Այսպիսով, մենք մուտքագրում ենք վերը նշված բանաձևը B9-ում, այն քաշում ենք ներքև մնացած ժամանակահատվածների համար և ստանում ենք հետևյալ արդյունքը. Եթե համեմատեք Տոկոսներ սյունակների թվերը (ձախում` սովորական անուիտետ և աջ կողմում` անուիտետ, ապա կնկատեք, որ տոկոսները մի փոքր ավելի ցածր են, երբ վճարում եք ժամանակաշրջանի սկզբում:
Excel IPMT ֆունկցիան չի աշխատում
Եթե ձեր IPMT բանաձևը սխալ է թույլ տալիս, ամենայն հավանականությամբ, դա կլինի հետևյալներից մեկը.
- #NUM! սխալ է տեղի ունենում, երբ per արգումենտը դուրս է 1-ից nper տիրույթից:
- #VALUE! սխալ է առաջանում, եթե արգումենտներից որևէ մեկը թվային չէ:
Այդպես եք օգտագործում IPMT ֆունկցիան Excel-ում: Այս ձեռնարկում քննարկված բանաձևերին ավելի մոտիկից ծանոթանալու համար կարող եք ներբեռնել մեր Excel IPMT ֆունկցիայի նմուշի աշխատանքային գիրքը: Շնորհակալ եմ կարդալու համար և հուսով եմ, որ հաջորդ շաբաթ կտեսնենք ձեզ մեր բլոգում:

