ಪರಿವಿಡಿ
ಸಾಲ ಅಥವಾ ಅಡಮಾನದ ಮೇಲಿನ ಆವರ್ತಕ ಪಾವತಿಯ ಬಡ್ಡಿ ಭಾಗವನ್ನು ಕಂಡುಹಿಡಿಯಲು Excel ನಲ್ಲಿ IPMT ಕಾರ್ಯವನ್ನು ಹೇಗೆ ಬಳಸುವುದು ಎಂಬುದನ್ನು ಟ್ಯುಟೋರಿಯಲ್ ತೋರಿಸುತ್ತದೆ.
ನೀವು ಸಾಲವನ್ನು ತೆಗೆದುಕೊಂಡಾಗ, ಅದು ಅಡಮಾನ, ಗೃಹ ಸಾಲ ಅಥವಾ ಕಾರ್ ಲೋನ್ ಆಗಿರಲಿ, ನೀವು ಮೂಲತಃ ಎರವಲು ಪಡೆದ ಮೊತ್ತ ಮತ್ತು ಅದರ ಮೇಲಿನ ಬಡ್ಡಿಯನ್ನು ನೀವು ಮರುಪಾವತಿಸಬೇಕಾಗುತ್ತದೆ. ಸರಳವಾಗಿ ಹೇಳುವುದಾದರೆ, ಬಡ್ಡಿಯು ಯಾರೊಬ್ಬರ (ಸಾಮಾನ್ಯವಾಗಿ ಬ್ಯಾಂಕಿನ) ಹಣವನ್ನು ಬಳಸುವ ವೆಚ್ಚವಾಗಿದೆ.
ಸಾಲ ಪಾವತಿಯ ಬಡ್ಡಿಯ ಭಾಗವನ್ನು ಉಳಿದ ಬಾಕಿಯಿಂದ ಅವಧಿಯ ಬಡ್ಡಿದರವನ್ನು ಗುಣಿಸುವ ಮೂಲಕ ಹಸ್ತಚಾಲಿತವಾಗಿ ಲೆಕ್ಕಹಾಕಬಹುದು. ಆದರೆ ಮೈಕ್ರೋಸಾಫ್ಟ್ ಎಕ್ಸೆಲ್ ಇದಕ್ಕಾಗಿ ವಿಶೇಷ ಕಾರ್ಯವನ್ನು ಹೊಂದಿದೆ - IPMT ಕಾರ್ಯ. ಈ ಟ್ಯುಟೋರಿಯಲ್ ನಲ್ಲಿ, ನಾವು ಅದರ ಸಿಂಟ್ಯಾಕ್ಸ್ ಅನ್ನು ವಿವರವಾಗಿ ವಿವರಿಸುತ್ತೇವೆ ಮತ್ತು ನೈಜ-ಜೀವನದ ಸೂತ್ರದ ಉದಾಹರಣೆಗಳನ್ನು ಒದಗಿಸುತ್ತೇವೆ.
Excel IPMT ಫಂಕ್ಷನ್ - ಸಿಂಟ್ಯಾಕ್ಸ್ ಮತ್ತು ಮೂಲಭೂತ ಉಪಯೋಗಗಳು
IPMT ಎಕ್ಸೆಲ್ನ ಬಡ್ಡಿ ಪಾವತಿ ಕಾರ್ಯವಾಗಿದೆ. ಇದು ಒಂದು ನಿರ್ದಿಷ್ಟ ಅವಧಿಯಲ್ಲಿ ಸಾಲದ ಪಾವತಿಯ ಬಡ್ಡಿ ಮೊತ್ತವನ್ನು ಹಿಂದಿರುಗಿಸುತ್ತದೆ, ಬಡ್ಡಿ ದರ ಮತ್ತು ಪಾವತಿಯ ಒಟ್ಟು ಮೊತ್ತವು ಎಲ್ಲಾ ಅವಧಿಗಳಲ್ಲಿ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ.
ಫಂಕ್ಷನ್ನ ಹೆಸರನ್ನು ಉತ್ತಮವಾಗಿ ನೆನಪಿಟ್ಟುಕೊಳ್ಳಲು, "I" ಅನ್ನು ಗಮನಿಸಿ "ಬಡ್ಡಿ" ಗಾಗಿ ಮತ್ತು "PMT" "ಪಾವತಿ".
Excel ನಲ್ಲಿ IPMT ಕಾರ್ಯದ ಸಿಂಟ್ಯಾಕ್ಸ್ ಈ ಕೆಳಗಿನಂತಿರುತ್ತದೆ:
IPMT(ದರ, ಪ್ರತಿ, nper, pv, [fv], [ಪ್ರಕಾರ ])ಎಲ್ಲಿ:
- ದರ (ಅಗತ್ಯವಿದೆ) - ಪ್ರತಿ ಅವಧಿಗೆ ಸ್ಥಿರ ಬಡ್ಡಿ ದರ. ನೀವು ಅದನ್ನು ಶೇಕಡಾವಾರು ಅಥವಾ ದಶಮಾಂಶ ಸಂಖ್ಯೆಯಾಗಿ ಪೂರೈಸಬಹುದು.
ಉದಾಹರಣೆಗೆ, ನೀವು ವಾರ್ಷಿಕ ಸಾಲದ ಮೇಲೆ ವಾರ್ಷಿಕ ಪಾವತಿಗಳನ್ನು ಮಾಡಿದರೆ6 ಪ್ರತಿಶತ ಬಡ್ಡಿ ದರ, ದರ ಕ್ಕೆ 6% ಅಥವಾ 0.06 ಬಳಸಿ.
ನೀವು ಸಾಪ್ತಾಹಿಕ, ಮಾಸಿಕ ಅಥವಾ ತ್ರೈಮಾಸಿಕ ಪಾವತಿಗಳನ್ನು ಮಾಡಿದರೆ, ವಾರ್ಷಿಕ ದರವನ್ನು ವರ್ಷಕ್ಕೆ ಪಾವತಿ ಅವಧಿಗಳ ಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸಿ, ಈ ಉದಾಹರಣೆಯಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ. ನೀವು 6 ಪ್ರತಿಶತ ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರದೊಂದಿಗೆ ಸಾಲದ ಮೇಲೆ ತ್ರೈಮಾಸಿಕ ಪಾವತಿಗಳನ್ನು ಮಾಡಿದರೆ, ದರ ಕ್ಕೆ 6%/4 ಅನ್ನು ಬಳಸಿ.
- ಪ್ರತಿ (ಅಗತ್ಯವಿದೆ) - ನೀವು ಬಡ್ಡಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಬಯಸುವ ಅವಧಿ. ಇದು 1 ರಿಂದ nper ವ್ಯಾಪ್ತಿಯಲ್ಲಿ ಪೂರ್ಣಾಂಕವಾಗಿರಬೇಕು.
- Nper (ಅಗತ್ಯವಿದೆ) - ಸಾಲದ ಜೀವಿತಾವಧಿಯಲ್ಲಿ ಪಾವತಿಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆ.
- Pv (ಅಗತ್ಯವಿದೆ) - ಸಾಲ ಅಥವಾ ಹೂಡಿಕೆಯ ಪ್ರಸ್ತುತ ಮೌಲ್ಯ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಇದು ಸಾಲದ ಅಸಲು, ಅಂದರೆ ನೀವು ಎರವಲು ಪಡೆದ ಮೊತ್ತ.
- Fv (ಐಚ್ಛಿಕ) - ಭವಿಷ್ಯದ ಮೌಲ್ಯ, ಅಂದರೆ ಕೊನೆಯ ಪಾವತಿಯನ್ನು ಮಾಡಿದ ನಂತರ ಬಯಸಿದ ಬಾಕಿ. ಬಿಟ್ಟುಬಿಟ್ಟರೆ, ಅದನ್ನು ಶೂನ್ಯ (0) ಎಂದು ಸೂಚಿಸಲಾಗುತ್ತದೆ.
- ಪ್ರಕಾರ (ಐಚ್ಛಿಕ) - ಪಾವತಿಗಳು ಯಾವಾಗ ಬಾಕಿಯಿವೆ ಎಂಬುದನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸುತ್ತದೆ:
- 0 ಅಥವಾ ಬಿಟ್ಟುಬಿಡಲಾಗಿದೆ - ಪಾವತಿಗಳನ್ನು ಮಾಡಲಾಗಿದೆ ಪ್ರತಿ ಅವಧಿಯ ಕೊನೆಯಲ್ಲಿ.
- 1 - ಪ್ರತಿ ಅವಧಿಯ ಆರಂಭದಲ್ಲಿ ಪಾವತಿಗಳನ್ನು ಮಾಡಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆಗೆ, ನೀವು $20,000 ಸಾಲವನ್ನು ಪಡೆದಿದ್ದರೆ , ನೀವು ಮುಂದಿನ 3 ವರ್ಷಗಳಲ್ಲಿ 6% ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರದೊಂದಿಗೆ ವಾರ್ಷಿಕ ಕಂತುಗಳಲ್ಲಿ ಪಾವತಿಸಬೇಕು, 1 ನೇ ವರ್ಷದ ಪಾವತಿಯ ಬಡ್ಡಿ ಭಾಗವನ್ನು ಈ ಸೂತ್ರದೊಂದಿಗೆ ಲೆಕ್ಕ ಹಾಕಬಹುದು:
=IPMT(6%, 1, 3, 20000)
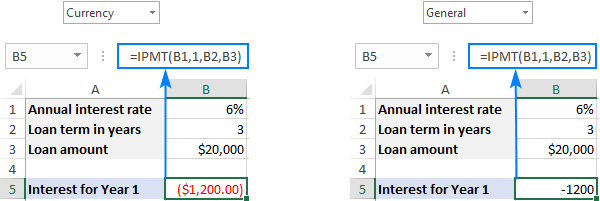
ಸಂಖ್ಯೆಗಳನ್ನು ನೇರವಾಗಿ ಸೂತ್ರಕ್ಕೆ ಪೂರೈಸುವ ಬದಲು, ನೀವು ಮಾಡಬಹುದುಕೆಲವು ಪೂರ್ವನಿರ್ಧರಿತ ಸೆಲ್ಗಳಲ್ಲಿ ಅವುಗಳನ್ನು ಇನ್ಪುಟ್ ಮಾಡಿ ಮತ್ತು ಕೆಳಗಿನ ಸ್ಕ್ರೀನ್ಶಾಟ್ನಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಆ ಸೆಲ್ಗಳನ್ನು ಉಲ್ಲೇಖಿಸಿ.
ನಗದು ಹರಿವು ಚಿಹ್ನೆಯ ಸಂಪ್ರದಾಯಕ್ಕೆ ಅನುಗುಣವಾಗಿ, ನೀವು ಪಾವತಿಸುವ ಕಾರಣ ಫಲಿತಾಂಶವನ್ನು ಋಣಾತ್ಮಕ ಸಂಖ್ಯೆಯಾಗಿ ಹಿಂತಿರುಗಿಸಲಾಗುತ್ತದೆ ಈ ಹಣದಿಂದ. ಪೂರ್ವನಿಯೋಜಿತವಾಗಿ, ಕೆಳಗಿನ ಸ್ಕ್ರೀನ್ಶಾಟ್ನ ಎಡ ಭಾಗದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಇದನ್ನು ಕೆಂಪು ಬಣ್ಣದಲ್ಲಿ ಹೈಲೈಟ್ ಮಾಡಲಾಗಿದೆ ಮತ್ತು ಆವರಣದಲ್ಲಿ ( ಕರೆನ್ಸಿ ಋಣಾತ್ಮಕ ಸಂಖ್ಯೆಗಳಿಗೆ ಫಾರ್ಮ್ಯಾಟ್) ಸುತ್ತುವರಿದಿದೆ. ಬಲಭಾಗದಲ್ಲಿ, ನೀವು ಸಾಮಾನ್ಯ ಫಾರ್ಮ್ಯಾಟ್ನಲ್ಲಿ ಅದೇ ಸೂತ್ರದ ಫಲಿತಾಂಶವನ್ನು ನೋಡಬಹುದು.
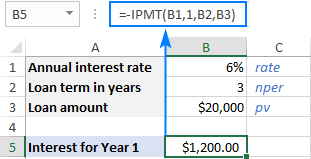
ನೀವು <8 ನಂತೆ ಆಸಕ್ತಿಯನ್ನು ಪಡೆಯಲು ಬಯಸಿದರೆ>ಧನಾತ್ಮಕ ಸಂಖ್ಯೆ , ಸಂಪೂರ್ಣ IPMT ಕಾರ್ಯ ಅಥವಾ pv ವಾದದ ಮೊದಲು ಮೈನಸ್ ಚಿಹ್ನೆಯನ್ನು ಹಾಕಿ:
=-IPMT(6%, 1, 3, 20000)
ಅಥವಾ
=IPMT(6%, 1, 3, -20000)
ಎಕ್ಸೆಲ್ನಲ್ಲಿ IPMT ಸೂತ್ರವನ್ನು ಬಳಸುವ ಉದಾಹರಣೆಗಳು
ಈಗ ನಿಮಗೆ ಮೂಲಗಳು ತಿಳಿದಿವೆ, ವಿವಿಧ ಆಸಕ್ತಿಯ ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯಲು IPMT ಕಾರ್ಯವನ್ನು ಹೇಗೆ ಬಳಸುವುದು ಎಂದು ನೋಡೋಣ ಪಾವತಿಯ ಆವರ್ತನಗಳು ಮತ್ತು ಸಾಲದ ಪರಿಸ್ಥಿತಿಗಳನ್ನು ಹೇಗೆ ಬದಲಾಯಿಸುವುದು ಸಂಭಾವ್ಯ ಆಸಕ್ತಿಯನ್ನು ಬದಲಾಯಿಸುತ್ತದೆ.
ನಾವು ಧುಮುಕುವ ಮೊದಲು, ಆವರ್ತಕ ಒಟ್ಟು ಮೊತ್ತವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ PMT ಕಾರ್ಯದ ನಂತರ IPMT ಸೂತ್ರಗಳನ್ನು ಬಳಸುವುದು ಉತ್ತಮ ಎಂದು ಗಮನಿಸಬೇಕು ಪಾವತಿ (ಬಡ್ಡಿ + ಅಸಲು).
ವಿವಿಧ ಪಾವತಿ ಆವರ್ತನಗಳಿಗಾಗಿ IPMT ಸೂತ್ರ (ವಾರಗಳು, ತಿಂಗಳುಗಳು, ತ್ರೈಮಾಸಿಕಗಳು)
ಸಾಲ ಪಾವತಿಯ ಬಡ್ಡಿ ಭಾಗವನ್ನು ಸರಿಯಾಗಿ ಪಡೆಯಲು, ನೀವು ಯಾವಾಗಲೂ ವಾರ್ಷಿಕ ಬಡ್ಡಿಯನ್ನು ಪರಿವರ್ತಿಸಬೇಕು ಅನುಗುಣವಾದ ಅವಧಿಯ ದರಕ್ಕೆ ದರ ಮತ್ತು ಪಾವತಿಯ ಒಟ್ಟು ಸಂಖ್ಯೆಗೆ ವರ್ಷಗಳ ಸಂಖ್ಯೆಅವಧಿಗಳು:
- ದರ ವಾದಕ್ಕಾಗಿ, ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರವನ್ನು ಪ್ರತಿ ವರ್ಷ ಪಾವತಿಗಳ ಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸಿ, ಎರಡನೆಯದು ವರ್ಷಕ್ಕೆ ಸಂಯೋಜಿತ ಅವಧಿಗಳ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ.
- nper ವಾದಕ್ಕೆ , ವರ್ಷಕ್ಕೆ ಪಾವತಿಗಳ ಸಂಖ್ಯೆಯಿಂದ ವರ್ಷಗಳ ಸಂಖ್ಯೆಯನ್ನು ಗುಣಿಸಿ.
ಕೆಳಗಿನ ಕೋಷ್ಟಕವು ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ತೋರಿಸುತ್ತದೆ:
| ಪಾವತಿಯ ಆವರ್ತನ | ದರ ವಾದ | ಪ್ರತಿ ವಾದ |
| ಸಾಪ್ತಾಹಿಕ | ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ / 52 | ವರ್ಷಗಳು * 52 |
| ಮಾಸಿಕ | ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ / 12 | ವರ್ಷಗಳು * 12 |
| ತ್ರೈಮಾಸಿಕ | ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ / 4 | ವರ್ಷಗಳು * 4 |
| ಅರೆ-ವಾರ್ಷಿಕ | ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ / 2 | ವರ್ಷಗಳು * 2 |
ಉದಾಹರಣೆಗೆ, ಒಂದೇ ಸಾಲದ ಮೇಲೆ ನೀವು ಪಾವತಿಸಬೇಕಾದ ಬಡ್ಡಿಯ ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ ಆದರೆ ಬೇರೆ ಬೇರೆ ಪಾವತಿ ಆವರ್ತನಗಳು:
- ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ: 6%
- ಸಾಲದ ಅವಧಿ: 2 ವರ್ಷಗಳು
- ಸಾಲದ ಮೊತ್ತ: $20,000
- ಅವಧಿ: 1
ನಂತರ ಬಾಕಿ r ಕೊನೆಯ ಪಾವತಿಯು $0 ಆಗಿರಬೇಕು ( fv ವಾದವನ್ನು ಬಿಟ್ಟುಬಿಡಲಾಗಿದೆ), ಮತ್ತು ಪಾವತಿಗಳು ಪ್ರತಿ ಅವಧಿಯ ಕೊನೆಯಲ್ಲಿ ಬಾಕಿಯಿರುತ್ತವೆ ( ಟೈಪ್ ವಾದವನ್ನು ಬಿಟ್ಟುಬಿಡಲಾಗಿದೆ).
ಸಾಪ್ತಾಹಿಕ :
=IPMT(6%/52, 1, 2*52, 20000)
ಮಾಸಿಕ :
=IPMT(6%/12, 1, 2*12, 20000)
ತ್ರೈಮಾಸಿಕ :
=IPMT(6%/4, 1, 2*4, 20000)
ಅರೆ-ವಾರ್ಷಿಕ :
=IPMT(6%/2, 1, 2*2, 20000)
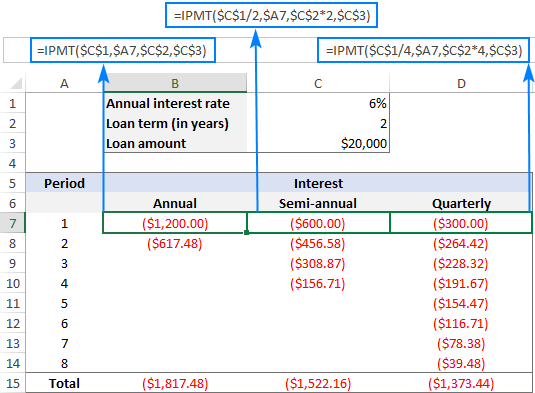
ಕೆಳಗಿನ ಸ್ಕ್ರೀನ್ಶಾಟ್ ಅನ್ನು ನೋಡಿದಾಗ, ಬಡ್ಡಿಯ ಮೊತ್ತವನ್ನು ನೀವು ಗಮನಿಸಬಹುದು ಪ್ರತಿ ನಂತರದ ಅವಧಿಯಲ್ಲಿ ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಇದುಏಕೆಂದರೆ ಯಾವುದೇ ಪಾವತಿಯು ಸಾಲದ ಮೂಲವನ್ನು ಕಡಿಮೆ ಮಾಡಲು ಕೊಡುಗೆ ನೀಡುತ್ತದೆ ಮತ್ತು ಇದು ಬಡ್ಡಿಯನ್ನು ಲೆಕ್ಕಹಾಕುವ ಉಳಿದ ಬಾಕಿಯನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ.
ಹಾಗೆಯೇ, ಅದೇ ಸಾಲದ ಮೇಲೆ ಪಾವತಿಸಬೇಕಾದ ಒಟ್ಟು ಬಡ್ಡಿಯ ಮೊತ್ತವು ವಾರ್ಷಿಕ, ಅರೆ-ವಾರ್ಷಿಕಕ್ಕೆ ಭಿನ್ನವಾಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ದಯವಿಟ್ಟು ಗಮನಿಸಿ ಮತ್ತು ತ್ರೈಮಾಸಿಕ ಕಂತುಗಳು:
IPMT ಫಂಕ್ಷನ್ನ ಪೂರ್ಣ ರೂಪ
ಈ ಉದಾಹರಣೆಯಲ್ಲಿ, ನಾವು ಅದೇ ಸಾಲಕ್ಕೆ ಬಡ್ಡಿಯನ್ನು ಲೆಕ್ಕ ಹಾಕಲಿದ್ದೇವೆ, ಅದೇ ಪಾವತಿ ಆವರ್ತನ , ಆದರೆ ವಿವಿಧ ವರ್ಷಾಶನ ಪ್ರಕಾರಗಳು (ನಿಯಮಿತ ಮತ್ತು ವರ್ಷಾಶನ-ಡ್ಯೂ). ಇದಕ್ಕಾಗಿ, ನಾವು IPMT ಫಂಕ್ಷನ್ನ ಪೂರ್ಣ ರೂಪವನ್ನು ಬಳಸಬೇಕಾಗುತ್ತದೆ.
ಪ್ರಾರಂಭಿಸಲು, ಇನ್ಪುಟ್ ಸೆಲ್ಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸೋಣ:
- B1 - ವಾರ್ಷಿಕ ಬಡ್ಡಿ ದರ 10>B2 - ವರ್ಷಗಳಲ್ಲಿ ಸಾಲದ ಅವಧಿ
- B3 - ವರ್ಷಕ್ಕೆ ಪಾವತಿಗಳ ಸಂಖ್ಯೆ
- B4 - ಸಾಲದ ಮೊತ್ತ ( pv )
- B5 - ಭವಿಷ್ಯದ ಮೌಲ್ಯ ( fv )
- B6 - ಪಾವತಿಗಳು ಬಾಕಿಯಿದ್ದಾಗ ( ಪ್ರಕಾರ ):
- 0 - ಅವಧಿಯ ಕೊನೆಯಲ್ಲಿ (ನಿಯಮಿತ ವರ್ಷಾಶನ)
- 1 - ಅವಧಿಯ ಆರಂಭದಲ್ಲಿ (ವರ್ಷಾಶನ ಬಾಕಿ)
ಮೊದಲ ಅವಧಿಯ ಸಂಖ್ಯೆಯು A9 ನಲ್ಲಿದೆ ಎಂದು ಭಾವಿಸಿದರೆ, ನಮ್ಮ ಆಸಕ್ತಿಯ ಸೂತ್ರವು ಈ ಕೆಳಗಿನಂತೆ ಹೋಗುತ್ತದೆ:
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
ಗಮನಿಸಿ. ನೀವು ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಅವಧಿಗೆ IPMT ಸೂತ್ರವನ್ನು ಬಳಸಲು ಯೋಜಿಸಿದರೆ, ದಯವಿಟ್ಟು ಸೆಲ್ ಉಲ್ಲೇಖಗಳನ್ನು ನೆನಪಿನಲ್ಲಿಡಿ. ಇನ್ಪುಟ್ ಸೆಲ್ಗಳ ಎಲ್ಲಾ ಉಲ್ಲೇಖಗಳು ಸಂಪೂರ್ಣವಾಗಿರಬೇಕು (ಡಾಲರ್ ಚಿಹ್ನೆಯೊಂದಿಗೆ) ಆದ್ದರಿಂದ ಅವುಗಳನ್ನು ಆ ಕೋಶಗಳಿಗೆ ಲಾಕ್ ಮಾಡಲಾಗುತ್ತದೆ. ಪ್ರತಿ ವಾದವು ಸಾಪೇಕ್ಷ ಸೆಲ್ ಉಲ್ಲೇಖವಾಗಿರಬೇಕು (A9 ನಂತಹ ಡಾಲರ್ ಚಿಹ್ನೆ ಇಲ್ಲದೆ) ಏಕೆಂದರೆ ಅದು ಬದಲಾಗಬೇಕುಸೂತ್ರವನ್ನು ನಕಲಿಸಲಾದ ಸಾಲಿನ ಸಾಪೇಕ್ಷ ಸ್ಥಾನ.
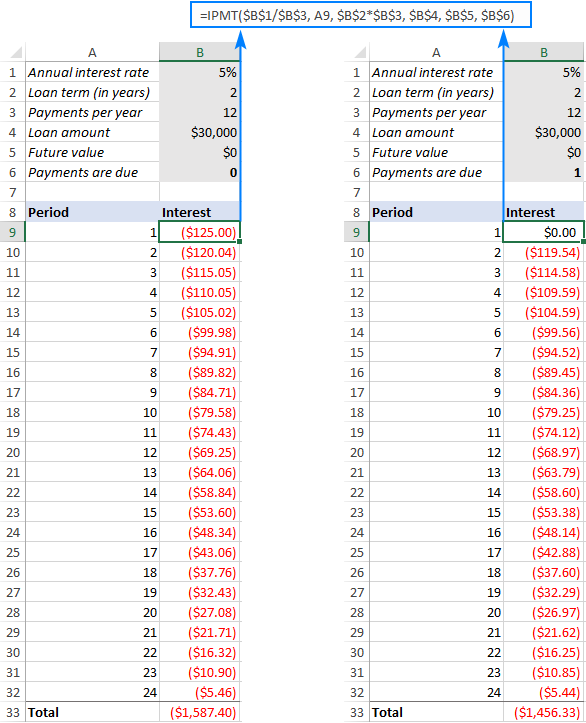
ಆದ್ದರಿಂದ, ನಾವು ಮೇಲಿನ ಸೂತ್ರವನ್ನು B9 ನಲ್ಲಿ ನಮೂದಿಸಿ, ಉಳಿದ ಅವಧಿಗಳಿಗೆ ಅದನ್ನು ಎಳೆಯಿರಿ ಮತ್ತು ಕೆಳಗಿನ ಫಲಿತಾಂಶವನ್ನು ಪಡೆಯಿರಿ. ನೀವು ಆಸಕ್ತಿ ಕಾಲಮ್ಗಳಲ್ಲಿನ ಸಂಖ್ಯೆಗಳನ್ನು ಹೋಲಿಸಿದಲ್ಲಿ (ಎಡಭಾಗದಲ್ಲಿ ನಿಯಮಿತ ವರ್ಷಾಶನ ಮತ್ತು ಬಲಭಾಗದಲ್ಲಿ ವರ್ಷಾಶನ ಬಾಕಿ), ನೀವು ಅವಧಿಯ ಆರಂಭದಲ್ಲಿ ಪಾವತಿಸಿದಾಗ ಬಡ್ಡಿಯು ಸ್ವಲ್ಪ ಕಡಿಮೆಯಾಗಿದೆ ಎಂದು ನೀವು ಗಮನಿಸಬಹುದು.
Excel IPMT ಕಾರ್ಯವು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿಲ್ಲ
ನಿಮ್ಮ IPMT ಸೂತ್ರವು ದೋಷವನ್ನು ಎಸೆದರೆ, ಅದು ಈ ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಒಂದಾಗಿರಬಹುದು:
- #NUM! ದೋಷ ಸಂಭವಿಸುತ್ತದೆ ಪ್ರತಿ ವಾದವು 1 ರಿಂದ nper ವ್ಯಾಪ್ತಿಯಿಂದ ಹೊರಗಿದೆ.
- #VALUE! ಯಾವುದೇ ವಾದಗಳು ಸಂಖ್ಯಾತ್ಮಕವಲ್ಲದಿದ್ದಲ್ಲಿ ದೋಷ ಸಂಭವಿಸುತ್ತದೆ.
ನೀವು ಎಕ್ಸೆಲ್ನಲ್ಲಿ IPMT ಕಾರ್ಯವನ್ನು ಹೇಗೆ ಬಳಸುತ್ತೀರಿ. ಈ ಟ್ಯುಟೋರಿಯಲ್ ನಲ್ಲಿ ಚರ್ಚಿಸಲಾದ ಸೂತ್ರಗಳನ್ನು ಹತ್ತಿರದಿಂದ ನೋಡಲು, ನಮ್ಮ Excel IPMT ಕಾರ್ಯ ಮಾದರಿ ವರ್ಕ್ಬುಕ್ ಅನ್ನು ಡೌನ್ಲೋಡ್ ಮಾಡಲು ನಿಮಗೆ ಸ್ವಾಗತ. ಓದಿದ್ದಕ್ಕಾಗಿ ನಾನು ನಿಮಗೆ ಧನ್ಯವಾದಗಳು ಮತ್ತು ಮುಂದಿನ ವಾರ ನಮ್ಮ ಬ್ಲಾಗ್ನಲ್ಲಿ ನಿಮ್ಮನ್ನು ನೋಡುತ್ತೇನೆ ಎಂದು ಭಾವಿಸುತ್ತೇನೆ!

