บทช่วยสอนแสดงวิธีใช้ฟังก์ชัน IPMT ใน Excel เพื่อค้นหาส่วนดอกเบี้ยของการชำระเงินเป็นงวดสำหรับเงินกู้หรือการจำนอง

เมื่อใดก็ตามที่คุณกู้เงิน ไม่ว่าจะเป็นสินเชื่อจำนอง สินเชื่อบ้านหรือสินเชื่อรถยนต์ คุณต้องชำระเงินคืนตามจำนวนที่คุณยืมในตอนแรกพร้อมดอกเบี้ยที่เพิ่มเข้ามา พูดง่ายๆ ก็คือ ดอกเบี้ยคือค่าใช้จ่ายในการใช้เงินของใครบางคน (โดยปกติจะเป็นของธนาคาร)

ส่วนดอกเบี้ยของการชำระเงินกู้สามารถคำนวณได้ด้วยตนเองโดยการคูณอัตราดอกเบี้ยของงวดด้วยยอดคงเหลือ แต่ Microsoft Excel มีฟังก์ชันพิเศษสำหรับสิ่งนี้ - ฟังก์ชัน IPMT ในบทช่วยสอนนี้ เราจะอธิบายเชิงลึกเกี่ยวกับไวยากรณ์และให้ตัวอย่างสูตรในชีวิตจริง

ฟังก์ชัน Excel IPMT - ไวยากรณ์และการใช้งานพื้นฐาน

IPMT เป็นฟังก์ชันการจ่ายดอกเบี้ยของ Excel ส่งกลับจำนวนดอกเบี้ยของการชำระเงินกู้ในช่วงเวลาที่กำหนด โดยสมมติว่าอัตราดอกเบี้ยและจำนวนเงินรวมของการชำระเงินคงที่ในทุกงวด

เพื่อให้จำชื่อฟังก์ชันได้ดีขึ้น โปรดสังเกตว่า "I" หมายถึง สำหรับ "ดอกเบี้ย" และ "PMT" สำหรับ "การชำระเงิน"

ไวยากรณ์ของฟังก์ชัน IPMT ใน Excel มีดังนี้:

ที่ไหน:

• อัตรา (จำเป็น) - อัตราดอกเบี้ยคงที่ต่องวด คุณสามารถระบุเป็นเปอร์เซ็นต์หรือเลขทศนิยม

  ตัวอย่างเช่น หากคุณชำระเงิน รายปี สำหรับเงินกู้เป็นรายปีอัตราดอกเบี้ย 6 เปอร์เซ็นต์ ใช้ 6% หรือ 0.06 สำหรับ อัตรา

  หากคุณชำระเงินเป็นรายสัปดาห์ รายเดือน หรือรายไตรมาส ให้หารอัตรารายปีด้วยจำนวนงวดการชำระเงินต่อปี ดังตัวอย่างนี้ สมมติว่า หากคุณชำระเงิน รายไตรมาส สำหรับเงินกู้ที่มีอัตราดอกเบี้ยต่อปีที่ 6 เปอร์เซ็นต์ ให้ใช้ 6%/4 สำหรับ อัตรา

• ต่อ (จำเป็น) - ระยะเวลาที่คุณต้องการคำนวณดอกเบี้ย ต้องเป็นจำนวนเต็มในช่วงตั้งแต่ 1 ถึง nper
• Nper (จำเป็น) - จำนวนการชำระเงินทั้งหมดตลอดอายุของเงินกู้
• Pv (จำเป็น) - มูลค่าปัจจุบันของเงินกู้หรือการลงทุน กล่าวอีกนัยหนึ่ง คือเงินต้นของเงินกู้ เช่น จำนวนเงินที่คุณยืม
• Fv (ไม่บังคับ) - มูลค่าในอนาคต เช่น ยอดคงเหลือที่ต้องการหลังจากชำระเงินครั้งล่าสุด หากละเว้น แสดงว่าเป็นศูนย์ (0)
• ประเภท (ไม่บังคับ) - ระบุเวลาที่ถึงกำหนดชำระเงิน:
  • 0 หรือละเว้น - ชำระเงินแล้ว เมื่อสิ้นสุดแต่ละงวด
  • 1 - ชำระเงินเมื่อเริ่มต้นแต่ละงวด

ตัวอย่างเช่น หากคุณได้รับเงินกู้ $20,000 ซึ่งคุณต้องชำระเป็นงวด รายปี ในช่วง 3 ปีข้างหน้า โดยมีอัตราดอกเบี้ยต่อปีที่ 6% คุณสามารถคำนวณส่วนดอกเบี้ยของการชำระเงินในปีที่ 1 ได้ด้วยสูตรนี้:

=IPMT(6%, 1, 3, 20000)

แทนที่จะใส่ตัวเลขลงในสูตรโดยตรง คุณสามารถทำได้ป้อนข้อมูลลงในเซลล์ที่กำหนดไว้ล่วงหน้าบางเซลล์และอ้างอิงถึงเซลล์เหล่านั้นดังที่แสดงในภาพหน้าจอด้านล่าง

ตามหลักการของสัญญาณกระแสเงินสด ผลลัพธ์จะถูกส่งกลับเป็นตัวเลข ลบ เนื่องจากคุณชำระเงิน ออกเงินนี้ โดยค่าเริ่มต้น จะถูกเน้นด้วยสีแดงและอยู่ในวงเล็บ (รูปแบบ สกุลเงิน สำหรับตัวเลขที่เป็นค่าลบ) ดังที่แสดงในส่วนด้านซ้ายของภาพหน้าจอด้านล่าง ทางด้านขวา คุณสามารถดูผลลัพธ์ของสูตรเดียวกันในรูปแบบ ทั่วไป

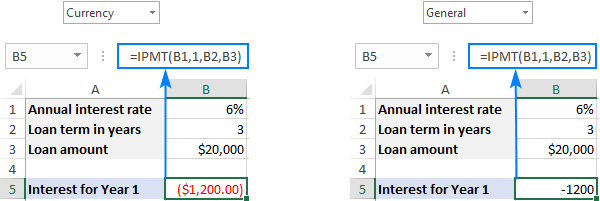
หากคุณต้องการได้รับดอกเบี้ยเป็น จำนวนบวก ใส่เครื่องหมายลบก่อนฟังก์ชัน IPMT ทั้งหมดหรืออาร์กิวเมนต์ pv :

=-IPMT(6%, 1, 3, 20000)

หรือ

=IPMT(6%, 1, 3, -20000)

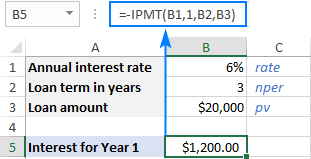
ตัวอย่างการใช้สูตร IPMT ใน Excel

เมื่อคุณทราบพื้นฐานแล้ว เรามาดูวิธีใช้ฟังก์ชัน IPMT เพื่อหาจำนวนดอกเบี้ยที่แตกต่างกัน ความถี่ในการชำระเงิน และการเปลี่ยนแปลงเงื่อนไขเงินกู้เปลี่ยนแปลงดอกเบี้ยที่อาจเกิดขึ้นได้อย่างไร

ก่อนที่เราจะเจาะลึก ควรสังเกตว่าควรใช้สูตร IPMT หลังจากฟังก์ชัน PMT ที่คำนวณยอดรวมของงวด การชำระเงิน (ดอกเบี้ย + เงินต้น)

สูตร IPMT สำหรับความถี่การชำระเงินต่างๆ (สัปดาห์ เดือน ไตรมาส)

เพื่อให้ได้ส่วนดอกเบี้ยของสิทธิ์การชำระเงินกู้ คุณควรแปลงดอกเบี้ยรายปีเสมอ อัตราตามระยะเวลาที่สอดคล้องกันและจำนวนปีถึงจำนวนการชำระเงินทั้งหมดงวด:

• สำหรับอาร์กิวเมนต์ อัตรา ให้หารอัตราดอกเบี้ยต่อปีด้วยจำนวนงวดที่ชำระต่อปี โดยถือว่างวดหลังเท่ากับจำนวนงวดทบต้นต่อปี
• สำหรับ อาร์กิวเมนต์ nper ให้คูณจำนวนปีด้วยจำนวนการชำระเงินต่อปี

ตารางต่อไปนี้แสดงการคำนวณ:

ตัวอย่างเช่น ลองหาจำนวนดอกเบี้ยที่คุณจะต้องจ่ายสำหรับเงินกู้ก้อนเดียวกันแต่ต่างกัน ความถี่ในการชำระเงิน:

• อัตราดอกเบี้ยต่อปี: 6%
• ระยะเวลาเงินกู้: 2 ปี
• จำนวนเงินกู้: $20,000
• ระยะเวลา: 1

ยอดหลัง r การชำระเงินครั้งสุดท้ายจะเป็น $0 (ไม่ต้องระบุอาร์กิวเมนต์ fv ) และการชำระเงินจะครบกำหนดเมื่อสิ้นสุดแต่ละงวด (ไม่ต้องระบุอาร์กิวเมนต์ type )

=IPMT(6%/52, 1, 2*52, 20000)

รายเดือน :

=IPMT(6%/12, 1, 2*12, 20000)

รายไตรมาส :

=IPMT(6%/4, 1, 2*4, 20000)

รายครึ่งปี :

=IPMT(6%/2, 1, 2*2, 20000)

ดูภาพหน้าจอด้านล่าง คุณจะสังเกตได้ว่าจำนวนดอกเบี้ย ลดลงในแต่ละงวดที่ตามมา นี่คือเนื่องจากการชำระเงินใด ๆ มีส่วนช่วยลดเงินต้นของเงินกู้ และทำให้ยอดคงเหลือที่คำนวณดอกเบี้ยลดลง

นอกจากนี้ โปรดทราบว่าจำนวนดอกเบี้ยทั้งหมดที่ต้องชำระสำหรับเงินกู้เดียวกันจะแตกต่างกันสำหรับรายปี รายครึ่งปี และการผ่อนชำระรายไตรมาส:

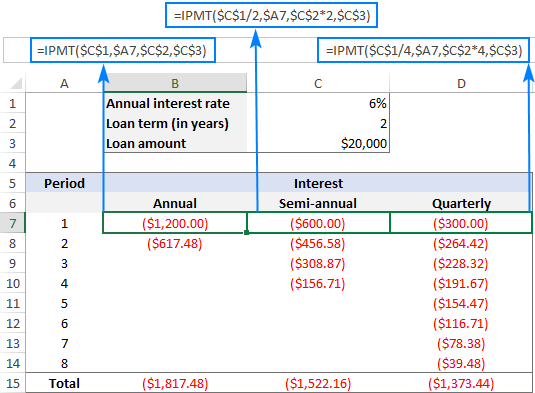
รูปแบบเต็มรูปแบบของฟังก์ชัน IPMT

ในตัวอย่างนี้ เราจะคำนวณดอกเบี้ยสำหรับเงินกู้ก้อนเดียวกัน ความถี่ในการชำระเท่ากัน แต่ประเภทเงินงวดต่างกัน (ปกติและเงินงวดถึงกำหนดชำระ) สำหรับสิ่งนี้ เราจะต้องใช้ฟังก์ชัน IPMT แบบเต็ม

ในการเริ่มต้น ให้กำหนดเซลล์อินพุต:

• B1 - อัตราดอกเบี้ยรายปี
• B2 - ระยะเวลาเงินกู้ในปี
• B3 - จำนวนการชำระเงินต่อปี
• B4 - จำนวนเงินกู้ ( pv )
• B5 - มูลค่าในอนาคต ( fv )
• B6 - เมื่อถึงกำหนดชำระเงิน ( ประเภท ):
  • 0 - เมื่อสิ้นสุดงวด (เงินงวดปกติ)
  • 1 - เมื่อต้นงวด (ครบกำหนดชำระ)

สมมติว่าหมายเลขงวดแรกอยู่ใน A9 สูตรดอกเบี้ยของเราจะเป็นดังนี้:

=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)

หมายเหตุ หากคุณวางแผนที่จะใช้สูตร IPMT มากกว่าหนึ่งช่วงเวลา โปรดคำนึงถึงการอ้างอิงเซลล์ การอ้างอิงทั้งหมดไปยังเซลล์อินพุตจะต้องเป็นแบบสัมบูรณ์ (โดยมีเครื่องหมายดอลลาร์) ดังนั้นการอ้างอิงทั้งหมดจะถูกล็อกไว้ที่เซลล์เหล่านั้น อาร์กิวเมนต์ ต่อ ต้องเป็นการอ้างอิงเซลล์แบบสัมพัทธ์ (โดยไม่มีเครื่องหมายดอลลาร์ เช่น A9) เนื่องจากควรเปลี่ยนตามตำแหน่งสัมพัทธ์ของแถวที่มีการคัดลอกสูตร

ดังนั้นเราจึงป้อนสูตรข้างต้นใน B9 ลากลงมาตามระยะเวลาที่เหลือ และรับผลลัพธ์ต่อไปนี้ หากคุณเปรียบเทียบตัวเลขในคอลัมน์ ดอกเบี้ย (เงินงวดปกติทางด้านซ้ายและเงินงวดที่ครบกำหนดชำระทางด้านขวา) คุณจะสังเกตเห็นว่าดอกเบี้ยจะลดลงเล็กน้อยเมื่อคุณชำระเงินเมื่อต้นงวด<3

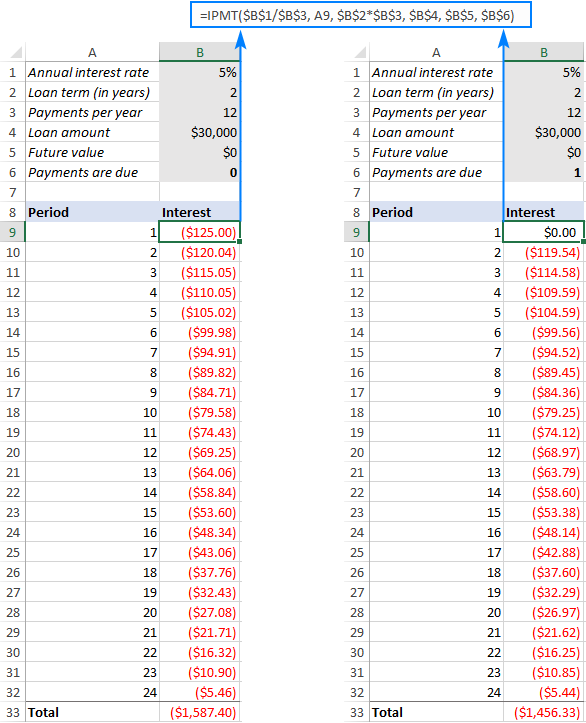
ฟังก์ชัน IPMT ของ Excel ไม่ทำงาน

หากสูตร IPMT ของคุณแสดงข้อผิดพลาด เป็นไปได้มากว่าเป็นหนึ่งในรายการต่อไปนี้:

1. #NUM! เกิดข้อผิดพลาดคืออาร์กิวเมนต์ per อยู่นอกช่วง 1 ถึง nper .
2. #VALUE! ข้อผิดพลาดจะเกิดขึ้นหากอาร์กิวเมนต์ใดๆ ไม่ใช่ตัวเลข

นั่นคือวิธีที่คุณใช้ฟังก์ชัน IPMT ใน Excel หากต้องการดูสูตรที่กล่าวถึงในบทช่วยสอนนี้อย่างละเอียดยิ่งขึ้น คุณสามารถดาวน์โหลดสมุดงานตัวอย่างฟังก์ชัน Excel IPMT ของเราได้ ฉันขอขอบคุณสำหรับการอ่านและหวังว่าจะได้พบคุณในบล็อกของเราในสัปดาห์หน้า!