ટ્યુટોરીયલ બતાવે છે કે કેવી રીતે એક્સેલમાં IPMT ફંક્શનનો ઉપયોગ લોન અથવા મોર્ટગેજ પરની સામયિક ચુકવણીના વ્યાજનો ભાગ શોધવા માટે કરવો.

જ્યારે પણ તમે લોન લો, પછી તે મોર્ટગેજ હોય, હોમ લોન હોય કે કાર લોન હોય, તમારે મૂળ ઉછીની રકમ અને તેના ઉપર વ્યાજ ચૂકવવું પડશે. સાદા શબ્દોમાં, વ્યાજ એ કોઈના (સામાન્ય રીતે બેંકના) નાણાનો ઉપયોગ કરવાની કિંમત છે.

લોન ચુકવણીના વ્યાજના ભાગની ગણતરી સમયગાળાના વ્યાજ દરને બાકીની રકમ દ્વારા ગુણાકાર કરીને જાતે કરી શકાય છે. પરંતુ માઈક્રોસોફ્ટ એક્સેલ આ માટે એક વિશેષ કાર્ય ધરાવે છે - IPMT કાર્ય. આ ટ્યુટોરીયલમાં, અમે તેના વાક્યરચનાને સમજાવીને અને વાસ્તવિક જીવનના સૂત્ર ઉદાહરણો આપીને ઊંડાણપૂર્વક જઈશું.

Excel IPMT ફંક્શન - સિન્ટેક્સ અને મૂળભૂત ઉપયોગો

IPMT એ એક્સેલનું વ્યાજ ચુકવણી કાર્ય છે. તે આપેલ સમયગાળામાં લોનની ચુકવણીની વ્યાજની રકમ પરત કરે છે, વ્યાજ દર અને ચુકવણીની કુલ રકમ તમામ સમયગાળામાં સ્થિર છે એમ ધારીને.

ફંક્શનના નામને વધુ સારી રીતે યાદ રાખવા માટે, નોંધ લો કે "I" છે "વ્યાજ" અને "ચુકવણી" માટે "PMT" માટે.

એક્સેલમાં IPMT કાર્યનું વાક્યરચના નીચે મુજબ છે:

ક્યાં:

• દર (જરૂરી) - સમયગાળા દીઠ સતત વ્યાજ દર. તમે તેને ટકાવારી અથવા દશાંશ નંબર તરીકે આપી શકો છો.

  ઉદાહરણ તરીકે, જો તમે વાર્ષિક સાથે લોન પર વાર્ષિક ચૂકવણી કરો છો6 ટકા વ્યાજ દર, દર માટે 6% અથવા 0.06 નો ઉપયોગ કરો.

  જો તમે સાપ્તાહિક, માસિક અથવા ત્રિમાસિક ચૂકવણી કરો છો, તો વાર્ષિક દરને દર વર્ષે ચૂકવણીના સમયગાળાની સંખ્યા દ્વારા વિભાજીત કરો, આ ઉદાહરણમાં બતાવ્યા પ્રમાણે. કહો, જો તમે 6 ટકાના વાર્ષિક વ્યાજ દર સાથે લોન પર ત્રિમાસિક ચૂકવણી કરો છો, તો દર માટે 6%/4નો ઉપયોગ કરો.

• પ્રતિ (જરૂરી) - તે સમયગાળો કે જેના માટે તમે વ્યાજની ગણતરી કરવા માંગો છો. તે 1 થી nper ની રેન્જમાં પૂર્ણાંક હોવું આવશ્યક છે.
• Nper (જરૂરી) - લોનના જીવનકાળ દરમિયાન ચૂકવણીની કુલ સંખ્યા.<11
• Pv (જરૂરી) - લોન અથવા રોકાણનું વર્તમાન મૂલ્ય. બીજા શબ્દોમાં કહીએ તો, તે લોનની મુદ્દલ છે, એટલે કે તમે ઉધાર લીધેલી રકમ.
• Fv (વૈકલ્પિક) - ભાવિ મૂલ્ય, એટલે કે છેલ્લી ચુકવણી કર્યા પછી ઇચ્છિત બેલેન્સ. જો અવગણવામાં આવે, તો તે શૂન્ય (0) હોવાનું સૂચિત છે.
• પ્રકાર (વૈકલ્પિક) - ચુકવણી ક્યારે બાકી છે તે સ્પષ્ટ કરે છે:
  • 0 અથવા અવગણવામાં આવે છે - ચૂકવણી કરવામાં આવે છે દરેક સમયગાળાના અંતે.
  • 1 - દરેક સમયગાળાની શરૂઆતમાં ચૂકવણી કરવામાં આવે છે.

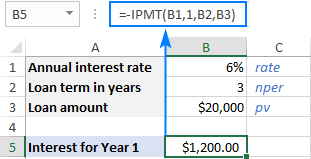
ઉદાહરણ તરીકે, જો તમને $20,000 ની લોન મળી હોય , જે તમારે આગામી 3 વર્ષ દરમિયાન 6% ના વાર્ષિક વ્યાજ દર સાથે વાર્ષિક હપ્તાઓમાં ચૂકવવું આવશ્યક છે, 1લા વર્ષની ચુકવણીના વ્યાજના ભાગની ગણતરી આ ફોર્મ્યુલા સાથે કરી શકાય છે:

=IPMT(6%, 1, 3, 20000)

ફર્મ્યુલામાં સીધો નંબર આપવાને બદલે, તમે કરી શકો છોતેમને કેટલાક પૂર્વવ્યાખ્યાયિત કોષોમાં ઇનપુટ કરો અને નીચેના સ્ક્રીનશોટમાં બતાવ્યા પ્રમાણે તે કોષોનો સંદર્ભ લો.

રોકડ પ્રવાહ સાઇન કન્વેન્શન અનુસાર, પરિણામ નકારાત્મક નંબર તરીકે પરત કરવામાં આવે છે કારણ કે તમે ચૂકવણી કરો છો આ પૈસા બહાર. મૂળભૂત રીતે, તે લાલ રંગમાં પ્રકાશિત થાય છે અને કૌંસમાં બંધ કરવામાં આવે છે ( ચલણ નકારાત્મક સંખ્યાઓ માટે ફોર્મેટ) નીચે સ્ક્રીનશોટના ડાબા ભાગમાં બતાવ્યા પ્રમાણે. જમણી બાજુએ, તમે સામાન્ય ફોર્મેટમાં સમાન ફોર્મ્યુલાનું પરિણામ જોઈ શકો છો.

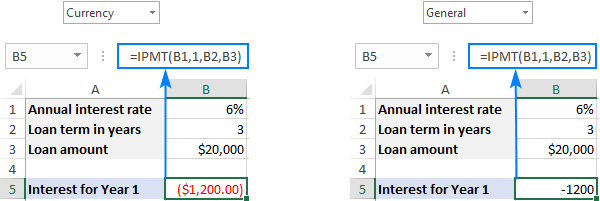
જો તમને <8 તરીકે રસ મેળવવાનું પસંદ હોય>પોઝિટિવ નંબર , સમગ્ર IPMT ફંક્શન અથવા pv દલીલ:

=-IPMT(6%, 1, 3, 20000)

અથવા

=IPMT(6%, 1, 3, -20000) <પહેલાં માઈનસ ચિહ્ન મૂકો 3>

એક્સેલમાં IPMT ફોર્મ્યુલાનો ઉપયોગ કરવાના ઉદાહરણો

હવે તમે બેઝિક્સ જાણો છો, ચાલો જોઈએ કે IPMT ફંક્શનનો ઉપયોગ વિવિધ માટે વ્યાજની રકમ શોધવા માટે કેવી રીતે કરવો. ચુકવણીની આવર્તન, અને કેવી રીતે લોનની પરિસ્થિતિઓમાં ફેરફાર સંભવિત વ્યાજને બદલે છે.

આપણે ડૂબકી લગાવીએ તે પહેલાં, એ નોંધવું જોઈએ કે પીએમટી ફંક્શન પછી IPMT ફોર્મ્યુલાનો ઉપયોગ કરવો શ્રેષ્ઠ છે જે સામયિકની કુલ રકમની ગણતરી કરે છે ચુકવણી (વ્યાજ + મુદ્દલ).

વિવિધ ચુકવણી આવર્તન (અઠવાડિયા, મહિના, ત્રિમાસિક) માટે IPMT ફોર્મ્યુલા

લોન ચુકવણીનો વ્યાજનો હિસ્સો યોગ્ય રીતે મેળવવા માટે, તમારે હંમેશા વાર્ષિક વ્યાજને કન્વર્ટ કરવું જોઈએ. અનુરૂપ સમયગાળાના દરનો દર અને ચૂકવણીની કુલ સંખ્યાના વર્ષોની સંખ્યાસમયગાળો:

• દર દલીલ માટે, વાર્ષિક વ્યાજ દરને દર વર્ષે ચૂકવણીની સંખ્યા દ્વારા વિભાજિત કરો, એમ ધારી રહ્યા છીએ કે બાદમાં પ્રતિ વર્ષ ચક્રવૃદ્ધિ સમયગાળાની સંખ્યા જેટલી છે.
• nper દલીલ માટે, વર્ષની સંખ્યાને દર વર્ષે ચૂકવણીની સંખ્યા વડે ગુણાકાર કરો.

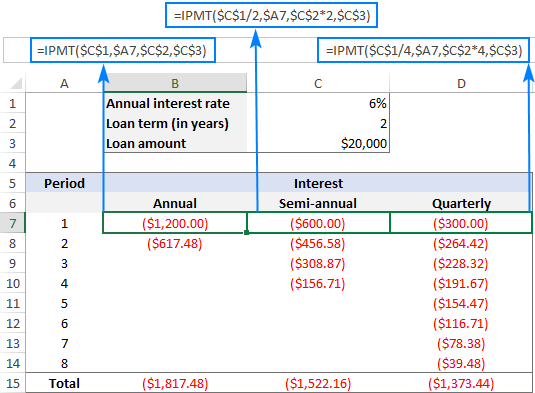
નીચેનું કોષ્ટક ગણતરીઓ બતાવે છે:

ઉદાહરણ તરીકે, ચાલો જોઈએ કે તમારે સમાન લોન પર વ્યાજની કેટલી રકમ ચૂકવવી પડશે પરંતુ અલગ અલગ ચુકવણીની આવર્તન:

• વાર્ષિક વ્યાજ દર: 6%
• લોન સમયગાળો: 2 વર્ષ
• લોન રકમ: $20,000
• કાળ: 1<11

બેલેન્સ પછી r છેલ્લી ચુકવણી $0 હોવી જોઈએ ( fv દલીલ અવગણવામાં આવી છે), અને ચૂકવણી દરેક સમયગાળાના અંતે બાકી છે ( પ્રકાર દલીલ અવગણવામાં આવી છે).

સાપ્તાહિક :

=IPMT(6%/52, 1, 2*52, 20000)

માસિક :

=IPMT(6%/12, 1, 2*12, 20000)

ત્રિમાસિક :

=IPMT(6%/4, 1, 2*4, 20000)

દરેક અનુગામી સમયગાળા સાથે ઘટે છે. આ છેકારણ કે કોઈપણ ચુકવણી લોનના મુદ્દલને ઘટાડવામાં ફાળો આપે છે, અને આ બાકીની રકમ ઘટાડે છે જેના પર વ્યાજની ગણતરી કરવામાં આવે છે.

આ ઉપરાંત, કૃપા કરીને નોંધ લો કે સમાન લોન પર ચૂકવવાપાત્ર વ્યાજની કુલ રકમ વાર્ષિક, અર્ધ-વાર્ષિક માટે અલગ છે. અને ત્રિમાસિક હપ્તાઓ:

IPMT કાર્યનું સંપૂર્ણ સ્વરૂપ

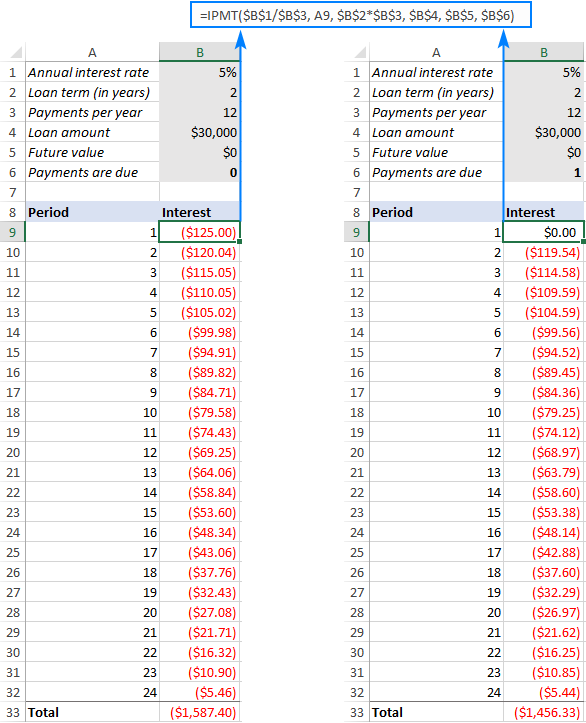
આ ઉદાહરણમાં, આપણે સમાન લોન માટે વ્યાજની ગણતરી કરવા જઈ રહ્યા છીએ, સમાન ચુકવણી આવર્તન , પરંતુ વિવિધ વાર્ષિકી પ્રકારો (નિયમિત અને વાર્ષિકી બાકી). આ માટે, આપણે IPMT ફંક્શનના સંપૂર્ણ સ્વરૂપનો ઉપયોગ કરવો પડશે.

શરૂઆત કરવા માટે, ચાલો ઇનપુટ કોષોને વ્યાખ્યાયિત કરીએ:

• B1 - વાર્ષિક વ્યાજ દર
• B2 - વર્ષોમાં લોનની મુદત
• B3 - દર વર્ષે ચૂકવણીની સંખ્યા
• B4 - લોનની રકમ ( pv )
• B5 - ભાવિ મૂલ્ય ( fv )
• B6 - જ્યારે ચૂકવણી બાકી હોય ( પ્રકાર ):
  • 0 - સમયગાળાના અંતે (નિયમિત વાર્ષિકી)
  • 1 - સમયગાળાની શરૂઆતમાં (નિયત વાર્ષિકી)

પ્રથમ પીરિયડ નંબર A9 માં છે એમ ધારી રહ્યા છીએ, અમારી રુચિ સૂત્ર નીચે મુજબ છે:

=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)

નોંધ. જો તમે એક કરતાં વધુ સમયગાળા માટે IPMT ફોર્મ્યુલાનો ઉપયોગ કરવાની યોજના ઘડી રહ્યા હો, તો કૃપા કરીને સેલ સંદર્ભોને ધ્યાનમાં રાખો. ઇનપુટ કોષોના તમામ સંદર્ભો નિરપેક્ષ (ડોલર ચિહ્ન સાથે) હોવા જોઈએ જેથી તે તે કોષો પર લૉક કરવામાં આવે. પ્રતિ દલીલ એ સંબંધિત સેલ સંદર્ભ (A9 જેવા ડૉલર ચિહ્ન વિના) હોવી જોઈએ કારણ કે તે આના આધારે બદલવી જોઈએ.પંક્તિની સાપેક્ષ સ્થિતિ કે જેમાં સૂત્રની નકલ કરવામાં આવી છે.

તેથી, અમે ઉપરનું સૂત્ર B9 માં દાખલ કરીએ છીએ, તેને બાકીના સમયગાળા માટે નીચે ખેંચીએ છીએ અને નીચેનું પરિણામ મેળવીએ છીએ. જો તમે વ્યાજ કૉલમ (ડાબી બાજુએ નિયમિત વાર્ષિકી અને જમણી બાજુએ વાર્ષિકી-બાકાત) માં સંખ્યાઓની સરખામણી કરો છો, તો તમે જોશો કે જ્યારે તમે સમયગાળાની શરૂઆતમાં ચૂકવણી કરો છો ત્યારે વ્યાજ થોડું ઓછું હોય છે.

Excel IPMT ફંક્શન કામ કરતું નથી

જો તમારું IPMT ફોર્મ્યુલા ભૂલ કરે છે, તો તે નીચેનામાંથી એક હોવાની સંભાવના છે:

1. #NUM! ભૂલ થાય છે તે પ્રતિ દલીલ શ્રેણી 1 થી nper ની બહાર છે.
2. #VALUE! જો કોઈપણ દલીલ બિન-સંખ્યાત્મક હોય તો ભૂલ થાય છે.

આ રીતે તમે Excel માં IPMT ફંક્શનનો ઉપયોગ કરો છો. આ ટ્યુટોરીયલમાં ચર્ચા કરેલ સૂત્રોને નજીકથી જોવા માટે, અમારી એક્સેલ IPMT ફંક્શન સેમ્પલ વર્કબુક ડાઉનલોડ કરવા માટે તમારું સ્વાગત છે. હું વાંચવા બદલ તમારો આભાર અને આશા રાખું છું કે તમને આવતા અઠવાડિયે અમારા બ્લોગ પર મળીશ!