Enhavtabelo
La lernilo montras kiel uzi la funkcion IPMT en Excel por trovi la interezan parton de perioda pago pri prunto aŭ hipoteko.
Kiam vi prenas prunton, ĉu ĝi estas hipoteko, domprunto aŭ aŭtoprunto, vi devas repagi la sumon, kiun vi origine pruntis, kaj interezojn aldone. En simplaj terminoj, interezo estas la kosto de uzado de ies (kutime banko) mono.
La interezparto de pruntpago povas esti kalkulita permane multobligante la interezoprocenton de la periodo per la restanta saldo. Sed Microsoft Excel havas specialan funkcion por tio - la funkcio IPMT. En ĉi tiu lernilo, ni profunde klarigos ĝian sintakson kaj disponigos realajn formulajn ekzemplojn.
Excel IPMT-funkcio - sintakso kaj bazaj uzoj
IPMT estas la funkcio de interezpago de Excel. Ĝi resendas la interezan kvanton de pruntpago en difinita periodo, supozante, ke la interezprocento kaj la totala kvanto de pago estas konstantaj en ĉiuj periodoj.
Por pli bone memori la nomon de la funkcio, rimarku, ke "I" staras. por "interezo" kaj "PMT" por "pago".
La sintakso de la funkcio IPMT en Excel estas jena:
IPMT(tarifo, po, nper, pv, [fv], [tipo ])Kie:
- Kiro (postulata) - la konstanta interezo por periodo. Vi povas provizi ĝin kiel procento aŭ dekuma nombro.
Ekzemple, se vi faras jarajn pagojn sur prunto kun ĉiujarainterezoprocento de 6 procentoj, uzu 6% aŭ 0,06 por kurzo .
Se vi faras semajnajn, monatajn aŭ kvaronjarajn pagojn, dividu la jaran indicon per la nombro da pagperiodoj jare, kiel montrite en ĉi tiu ekzemplo. Diru, se vi faras trimonatajn pagojn sur prunto kun jara interezo de 6 procentoj, uzu 6%/4 por kurzo .
- Po (postulata) - la periodo por kiu vi volas kalkuli la interezon. Ĝi devas esti entjero en la intervalo de 1 ĝis nper .
- Nper (postulata) - la totala nombro da pagoj dum la vivdaŭro de la prunto.
- Pv (postulata) - la nuna valoro de la prunto aŭ investo. Alivorte, ĝi estas la pruntĉefo, t.e. la sumo kiun vi pruntis.
- Fv (laŭvola) - la estonta valoro, t.e. la dezirata saldo post la lasta pago estas farita. Se ellasita, ĝi estas subkomprenata esti nul (0).
- Tipo (laŭvola) - precizigas kiam la pagoj estas pagendaj:
- 0 aŭ ellasita - pagoj estas faritaj je la fino de ĉiu periodo.
- 1 - pagoj estas faritaj komence de ĉiu periodo.
Ekzemple, se vi ricevis prunton de $20,000 , kiun vi devas pagi en jaraj partopagoj dum la venontaj 3 jaroj kun jara interezoprocento de 6%, la interezparto de la 1-a jara pago povas esti kalkulita per ĉi tiu formulo:
=IPMT(6%, 1, 3, 20000)
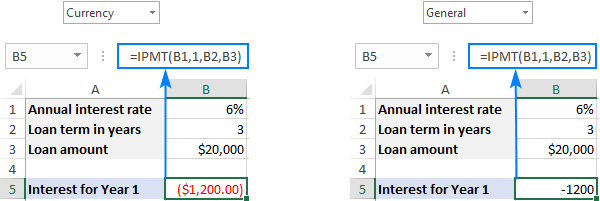
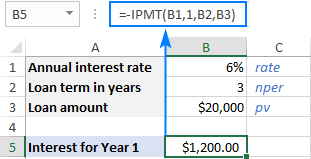
Anstataŭ liveri la nombrojn rekte en formulon, vi povasenigu ilin en iuj antaŭdifinitaj ĉeloj kaj referencu tiujn ĉelojn kiel montrite en la ekrankopio malsupre.
Konforme al la konvencio de monfluo-signo, la rezulto estas redonita kiel negativa nombro ĉar vi pagas eltiri ĉi tiun monon. Defaŭlte, ĝi estas elstarigita ruĝe kaj enfermita en krampoj (formato Monero por negativaj nombroj) kiel montrite en la maldekstra parto de la malsupra ekrankopio. Dekstre, vi povas vidi la rezulton de la sama formulo en la formato Ĝenerala .
Se vi preferas akiri intereson kiel pozitiva nombro , metu minuson antaŭ aŭ la tuta IPMT-funkcio aŭ la pv argumento:
=-IPMT(6%, 1, 3, 20000)
aŭ
=IPMT(6%, 1, 3, -20000)
Ekzemploj pri uzado de IPMT-formulo en Excel
Nun kiam vi konas la bazojn, ni vidu kiel uzi la IPMT-funkcion por trovi la kvanton de intereso por malsamaj frekvencoj de pago, kaj kiel ŝanĝi la pruntkondiĉojn ŝanĝas la eblan interezon.
Antaŭ ol ni plonĝi enen, oni devas rimarki, ke IPMT-formuloj estas plej bone uzataj post la PMT-funkcio, kiu kalkulas la totalan kvanton de periodaĵo. pago (interezo + ĉefo).
IPMT-formulo por malsamaj pagfrekvencoj (semajnoj, monatoj, kvaronoj)
Por ĝuste ricevi la interezan parton de pruntpago, vi ĉiam devas konverti la jaran interezon imposto al la responda periodo kaj la nombro da jaroj al la totala pagoperiodoj:
- Por la argumento kurzo , dividu la jaran interezoprocenton per la nombro da pagoj jare, supozante, ke ĉi-lasta egalas al la nombro da kunmetaj periodoj jare.
- Por la nper argumento , multipliku la nombron da jaroj per la nombro da pagoj jare.
La sekva tabelo montras la kalkulojn:
| Ofteco de pago | Kara argumento | Nper argumento |
| Semajna | jara intereso kurzo / 52 | jaroj * 52 |
| Monata | jara interezoprocento / 12 | jaroj * 12 |
| Kvarona | jara interezoprocento / 4 | jaroj * 4 |
| Dumjara | jara interezo / 2 | jaroj * 2 |
Ekzemple, ni trovu la kvanton da interezo, kiun vi devos pagi je la sama prunto sed en malsamaj pagfrekvencoj:
- Jara interezoprocento: 6%
- Pruntodaŭro: 2 jaroj
- Pruntkvanto: $20,000
- Periodo: 1
La bilanco post r la lasta pago devas esti $0 (la argumento fv ellasita), kaj la pagoj estas pagendaj je la fino de ĉiu periodo (la argumento tipo ellasita).
Ĉiusemajne :
=IPMT(6%/52, 1, 2*52, 20000)
Ĉiumonate :
=IPMT(6%/12, 1, 2*12, 20000)
Kvaronjare :
=IPMT(6%/4, 1, 2*4, 20000)
Dumjara :
=IPMT(6%/2, 1, 2*2, 20000)
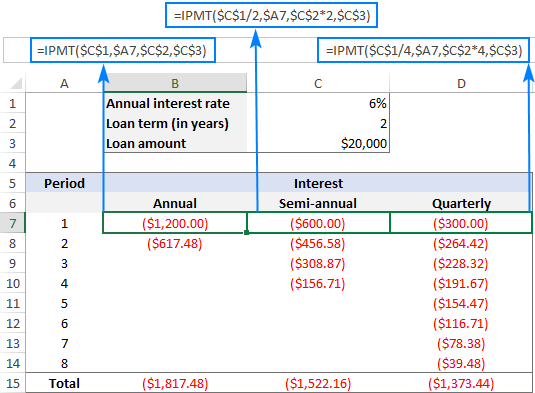
Rigardante la ekrankopion sube, vi povas rimarki, ke la intereza kvanto malpliiĝas kun ĉiu posta periodo. Ĉi tio estasĉar ĉiu pago kontribuas al redukto de la pruntoĉefo, kaj ĉi tio reduktas la restantan saldon, sur kiu estas kalkulita interezo.
Ankaŭ, bonvolu rimarki, ke la totala sumo de interezo pagenda pri la sama prunto diferencas por ĉiujara, duonjara. kaj trimonataj pagoj:
Plena formo de la funkcio IPMT
En ĉi tiu ekzemplo, ni kalkulos interezojn por la sama prunto, la sama pagfrekvenco , sed malsamaj anuitatspecoj (regula kaj anuitat-ŝuldata). Por tio, ni devos uzi la plenan formon de la funkcio IPMT.
Por komenci, ni difinu la enigajn ĉelojn:
- B1 - jara interezo
- B2 - pruntperiodo en jaroj
- B3 - nombro da pagoj jare
- B4 - pruntokvanto ( pv )
- B5 - estonta valoro ( fv )
- B6 - kiam la pagoj estas pagendaj ( tipo ):
- 0 - je la fino de periodo (regula anuitato)
- 1 - je la komenco de periodo (annuo-ŝuldata)
Supozinte, ke la unua perioda nombro estas en A9, nia interezformulo estas jene:
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
Notu. Se vi planas uzi la IPMT-formulon por pli ol unu periodo, bonvolu atenti la ĉelajn referencojn. Ĉiuj referencoj al la eniga ĉeloj devas esti absolutaj (kun la dolaro) do ili estas ŝlositaj al tiuj ĉeloj. La argumento po devas esti relativa ĉelreferenco (sen la dolarsigno kiel A9) ĉar ĝi devus ŝanĝiĝi surbaze de larelativa pozicio de vico al kiu la formulo estas kopiita.
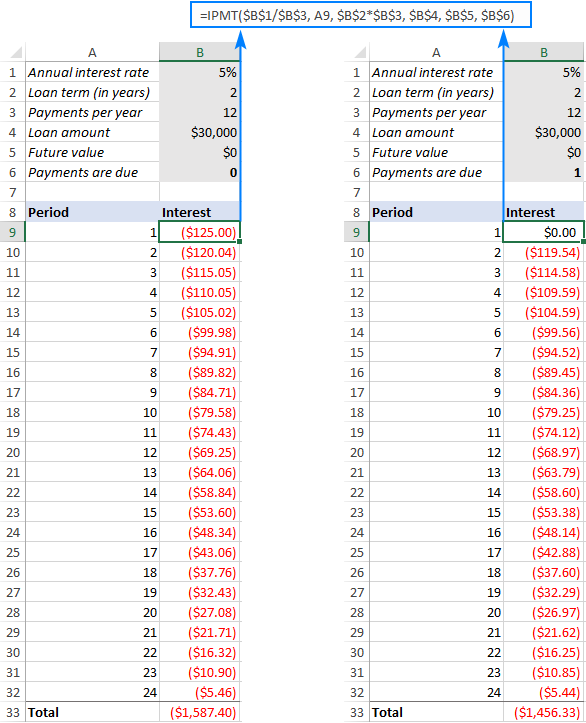
Do, ni enigas la supran formulon en B9, trenu ĝin malsupren por la ceteraj periodoj, kaj ricevas la sekvan rezulton. Se vi komparas la nombrojn en la kolumnoj Intereso (regula anuitato maldekstre kaj anuitato dekstre), vi rimarkos, ke interezo estas iom pli malalta kiam vi pagas komence de periodo.
Excel IPMT-funkcio ne funkcias
Se via IPMT-formulo ĵetas eraron, plej verŝajne ĝi estos unu el la jenaj:
- #NUM! eraro okazas se la argumento per estas ekster la intervalo 1 ĝis nper .
- #VALORO! eraro okazas se iu el la argumentoj estas nenumera.
Tiel vi uzas la funkcion IPMT en Excel. Por pli detale rigardi la formulojn diskutitajn en ĉi tiu lernilo, vi bonvenas elŝuti nian ekzemplan laborlibron de Excel IPMT. Mi dankas vin pro legado kaj esperas vidi vin en nia blogo venontsemajne!

