ਵਿਸ਼ਾ - ਸੂਚੀ
ਟਿਊਟੋਰਿਅਲ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ਕਰਜ਼ੇ ਜਾਂ ਮੌਰਗੇਜ 'ਤੇ ਸਮੇਂ-ਸਮੇਂ 'ਤੇ ਭੁਗਤਾਨ ਦੇ ਵਿਆਜ ਵਾਲੇ ਹਿੱਸੇ ਨੂੰ ਲੱਭਣ ਲਈ ਐਕਸਲ ਵਿੱਚ IPMT ਫੰਕਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਿਵੇਂ ਕਰਨੀ ਹੈ।
ਜਦੋਂ ਵੀ ਤੁਸੀਂ ਕੋਈ ਕਰਜ਼ਾ ਲੈਂਦੇ ਹੋ, ਭਾਵੇਂ ਇਹ ਇੱਕ ਮੌਰਗੇਜ, ਹੋਮ ਲੋਨ ਜਾਂ ਕਾਰ ਲੋਨ ਹੋਵੇ, ਤੁਹਾਨੂੰ ਅਸਲ ਵਿੱਚ ਉਧਾਰ ਲਈ ਗਈ ਰਕਮ ਅਤੇ ਇਸਦੇ ਉੱਪਰ ਵਿਆਜ ਦਾ ਭੁਗਤਾਨ ਕਰਨ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ। ਸਰਲ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਵਿਆਜ ਕਿਸੇ ਦੇ (ਆਮ ਤੌਰ 'ਤੇ ਕਿਸੇ ਬੈਂਕ ਦੇ) ਪੈਸੇ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਲਾਗਤ ਹੈ।
ਕਿਸੇ ਕਰਜ਼ੇ ਦੇ ਭੁਗਤਾਨ ਦੇ ਵਿਆਜ ਵਾਲੇ ਹਿੱਸੇ ਦੀ ਮਿਆਦ ਦੀ ਵਿਆਜ ਦਰ ਨੂੰ ਬਾਕੀ ਬਚੇ ਬਕਾਏ ਨਾਲ ਗੁਣਾ ਕਰਕੇ ਹੱਥੀਂ ਗਿਣਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਪਰ ਮਾਈਕਰੋਸਾਫਟ ਐਕਸਲ ਕੋਲ ਇਸਦੇ ਲਈ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਫੰਕਸ਼ਨ ਹੈ - IPMT ਫੰਕਸ਼ਨ. ਇਸ ਟਿਊਟੋਰਿਅਲ ਵਿੱਚ, ਅਸੀਂ ਇਸਦੇ ਸੰਟੈਕਸ ਨੂੰ ਸਮਝਾਉਣ ਅਤੇ ਅਸਲ-ਜੀਵਨ ਫਾਰਮੂਲੇ ਦੀਆਂ ਉਦਾਹਰਣਾਂ ਪ੍ਰਦਾਨ ਕਰਨ ਲਈ ਡੂੰਘਾਈ ਨਾਲ ਜਾਵਾਂਗੇ।
Excel IPMT ਫੰਕਸ਼ਨ - ਸੰਟੈਕਸ ਅਤੇ ਬੁਨਿਆਦੀ ਵਰਤੋਂ
IPMT ਐਕਸਲ ਦਾ ਵਿਆਜ ਭੁਗਤਾਨ ਕਾਰਜ ਹੈ। ਇਹ ਵਿਆਜ ਦਰ ਅਤੇ ਭੁਗਤਾਨ ਦੀ ਕੁੱਲ ਰਕਮ ਨੂੰ ਸਾਰੀਆਂ ਮਿਆਦਾਂ ਵਿੱਚ ਸਥਿਰ ਮੰਨਦੇ ਹੋਏ, ਇੱਕ ਦਿੱਤੀ ਮਿਆਦ ਵਿੱਚ ਕਰਜ਼ੇ ਦੀ ਅਦਾਇਗੀ ਦੀ ਵਿਆਜ ਰਕਮ ਵਾਪਸ ਕਰਦਾ ਹੈ।
ਫੰਕਸ਼ਨ ਦੇ ਨਾਮ ਨੂੰ ਬਿਹਤਰ ਢੰਗ ਨਾਲ ਯਾਦ ਰੱਖਣ ਲਈ, ਧਿਆਨ ਦਿਓ ਕਿ "I" ਹੈ "ਭੁਗਤਾਨ" ਲਈ "ਵਿਆਜ" ਅਤੇ "PMT" ਲਈ।
ਐਕਸਲ ਵਿੱਚ IPMT ਫੰਕਸ਼ਨ ਦਾ ਸੰਟੈਕਸ ਇਸ ਤਰ੍ਹਾਂ ਹੈ:
IPMT(ਦਰ, ਪ੍ਰਤੀ, nper, pv, [fv], [type ])ਕਿੱਥੇ:
- ਦਰ (ਲੋੜੀਂਦਾ) - ਪ੍ਰਤੀ ਅਵਧੀ ਸਥਾਈ ਵਿਆਜ ਦਰ। ਤੁਸੀਂ ਇਸਨੂੰ ਪ੍ਰਤੀਸ਼ਤ ਜਾਂ ਦਸ਼ਮਲਵ ਸੰਖਿਆ ਦੇ ਰੂਪ ਵਿੱਚ ਸਪਲਾਈ ਕਰ ਸਕਦੇ ਹੋ।
ਉਦਾਹਰਨ ਲਈ, ਜੇਕਰ ਤੁਸੀਂ ਕਰਜ਼ੇ 'ਤੇ ਸਾਲਾਨਾ ਸਾਲਾਨਾ ਭੁਗਤਾਨ ਕਰਦੇ ਹੋ6 ਪ੍ਰਤੀਸ਼ਤ ਦੀ ਵਿਆਜ ਦਰ, ਦਰ ਲਈ 6% ਜਾਂ 0.06 ਦੀ ਵਰਤੋਂ ਕਰੋ।
ਜੇਕਰ ਤੁਸੀਂ ਹਫਤਾਵਾਰੀ, ਮਾਸਿਕ ਜਾਂ ਤਿਮਾਹੀ ਭੁਗਤਾਨ ਕਰਦੇ ਹੋ, ਤਾਂ ਸਾਲਾਨਾ ਦਰ ਨੂੰ ਪ੍ਰਤੀ ਸਾਲ ਭੁਗਤਾਨ ਦੀ ਮਿਆਦ ਦੀ ਸੰਖਿਆ ਨਾਲ ਵੰਡੋ, ਜਿਵੇਂ ਕਿ ਇਸ ਉਦਾਹਰਨ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਕਹੋ, ਜੇਕਰ ਤੁਸੀਂ 6 ਪ੍ਰਤੀਸ਼ਤ ਦੀ ਸਾਲਾਨਾ ਵਿਆਜ ਦਰ ਨਾਲ ਕਰਜ਼ੇ 'ਤੇ ਤਿਮਾਹੀ ਭੁਗਤਾਨ ਕਰਦੇ ਹੋ, ਤਾਂ ਦਰ ਲਈ 6%/4 ਦੀ ਵਰਤੋਂ ਕਰੋ।
- ਪ੍ਰਤੀ (ਲੋੜੀਂਦੀ) - ਉਹ ਮਿਆਦ ਜਿਸ ਲਈ ਤੁਸੀਂ ਵਿਆਜ ਦੀ ਗਣਨਾ ਕਰਨਾ ਚਾਹੁੰਦੇ ਹੋ। ਇਹ 1 ਤੋਂ nper ਦੀ ਰੇਂਜ ਵਿੱਚ ਇੱਕ ਪੂਰਨ ਅੰਕ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।
- Nper (ਲੋੜੀਂਦਾ) - ਕਰਜ਼ੇ ਦੇ ਜੀਵਨ ਕਾਲ ਦੌਰਾਨ ਭੁਗਤਾਨਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ।
- Pv (ਲੋੜੀਂਦਾ) - ਕਰਜ਼ੇ ਜਾਂ ਨਿਵੇਸ਼ ਦਾ ਮੌਜੂਦਾ ਮੁੱਲ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਇਹ ਕਰਜ਼ਾ ਮੂਲ ਹੈ, ਅਰਥਾਤ ਉਹ ਰਕਮ ਜੋ ਤੁਸੀਂ ਉਧਾਰ ਲਈ ਸੀ।
- Fv (ਵਿਕਲਪਿਕ) - ਭਵਿੱਖ ਦਾ ਮੁੱਲ, ਭਾਵ ਆਖਰੀ ਭੁਗਤਾਨ ਕੀਤੇ ਜਾਣ ਤੋਂ ਬਾਅਦ ਲੋੜੀਂਦਾ ਬਕਾਇਆ। ਜੇਕਰ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸਦਾ ਮਤਲਬ ਜ਼ੀਰੋ (0) ਹੈ।
- ਕਿਸਮ (ਵਿਕਲਪਿਕ) - ਇਹ ਦੱਸਦਾ ਹੈ ਕਿ ਭੁਗਤਾਨ ਕਦੋਂ ਕਰਨੇ ਹਨ:
- 0 ਜਾਂ ਛੱਡੇ ਗਏ - ਭੁਗਤਾਨ ਕੀਤੇ ਜਾਂਦੇ ਹਨ। ਹਰੇਕ ਮਿਆਦ ਦੇ ਅੰਤ ਵਿੱਚ।
- 1 - ਭੁਗਤਾਨ ਹਰੇਕ ਮਿਆਦ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਕੀਤੇ ਜਾਂਦੇ ਹਨ।
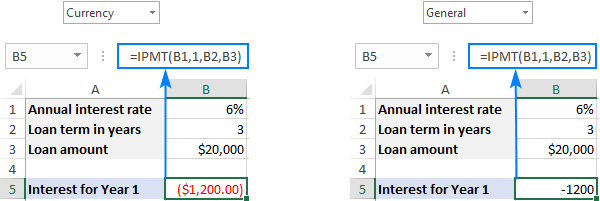
ਉਦਾਹਰਨ ਲਈ, ਜੇਕਰ ਤੁਹਾਨੂੰ $20,000 ਦਾ ਕਰਜ਼ਾ ਪ੍ਰਾਪਤ ਹੋਇਆ ਹੈ , ਜਿਸਦਾ ਤੁਹਾਨੂੰ ਅਗਲੇ 3 ਸਾਲਾਂ ਦੌਰਾਨ 6% ਦੀ ਸਲਾਨਾ ਵਿਆਜ ਦਰ ਨਾਲ ਸਾਲਾਨਾ ਕਿਸ਼ਤਾਂ ਵਿੱਚ ਭੁਗਤਾਨ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ, ਪਹਿਲੇ ਸਾਲ ਦੇ ਭੁਗਤਾਨ ਦੇ ਵਿਆਜ ਵਾਲੇ ਹਿੱਸੇ ਦੀ ਗਣਨਾ ਇਸ ਫਾਰਮੂਲੇ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ:
=IPMT(6%, 1, 3, 20000)
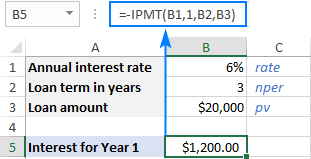
ਸੰਖਿਆਵਾਂ ਨੂੰ ਸਿੱਧੇ ਫਾਰਮੂਲੇ ਵਿੱਚ ਸਪਲਾਈ ਕਰਨ ਦੀ ਬਜਾਏ, ਤੁਸੀਂ ਕਰ ਸਕਦੇ ਹੋਉਹਨਾਂ ਨੂੰ ਕੁਝ ਪੂਰਵ-ਪਰਿਭਾਸ਼ਿਤ ਸੈੱਲਾਂ ਵਿੱਚ ਇਨਪੁਟ ਕਰੋ ਅਤੇ ਉਹਨਾਂ ਸੈੱਲਾਂ ਦਾ ਹਵਾਲਾ ਦਿਓ ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਸਕ੍ਰੀਨਸ਼ਾਟ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।
ਨਕਦ ਪ੍ਰਵਾਹ ਸੰਕੇਤ ਸੰਮੇਲਨ ਦੇ ਅਨੁਸਾਰ, ਨਤੀਜਾ ਇੱਕ ਨੈਗੇਟਿਵ ਨੰਬਰ ਵਜੋਂ ਵਾਪਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਤੁਸੀਂ ਭੁਗਤਾਨ ਕਰਦੇ ਹੋ ਇਸ ਪੈਸੇ ਨੂੰ ਬਾਹਰ. ਮੂਲ ਰੂਪ ਵਿੱਚ, ਇਹ ਲਾਲ ਰੰਗ ਵਿੱਚ ਉਜਾਗਰ ਕੀਤਾ ਗਿਆ ਹੈ ਅਤੇ ਬਰੈਕਟ ਵਿੱਚ ਬੰਦ ਹੈ ( ਮੁਦਰਾ ਨਕਾਰਾਤਮਕ ਸੰਖਿਆਵਾਂ ਲਈ ਫਾਰਮੈਟ) ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਸਕ੍ਰੀਨਸ਼ੌਟ ਦੇ ਖੱਬੇ ਹਿੱਸੇ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਸੱਜੇ ਪਾਸੇ, ਤੁਸੀਂ ਆਮ ਫਾਰਮੈਟ ਵਿੱਚ ਉਸੇ ਫਾਰਮੂਲੇ ਦਾ ਨਤੀਜਾ ਦੇਖ ਸਕਦੇ ਹੋ।
ਜੇਕਰ ਤੁਸੀਂ ਇੱਕ <8 ਦੇ ਰੂਪ ਵਿੱਚ ਦਿਲਚਸਪੀ ਲੈਣਾ ਚਾਹੁੰਦੇ ਹੋ>ਪਾਜ਼ਿਟਿਵ ਨੰਬਰ , ਪੂਰੇ IPMT ਫੰਕਸ਼ਨ ਜਾਂ pv ਆਰਗੂਮੈਂਟ:
=-IPMT(6%, 1, 3, 20000)
ਜਾਂ
=IPMT(6%, 1, 3, -20000) <ਅੱਗੇ ਇੱਕ ਘਟਾਓ ਦਾ ਚਿੰਨ੍ਹ ਲਗਾਓ। 3>
ਐਕਸਲ ਵਿੱਚ IPMT ਫਾਰਮੂਲੇ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀਆਂ ਉਦਾਹਰਨਾਂ
ਹੁਣ ਜਦੋਂ ਤੁਸੀਂ ਮੂਲ ਗੱਲਾਂ ਜਾਣਦੇ ਹੋ, ਆਓ ਦੇਖੀਏ ਕਿ ਵੱਖ-ਵੱਖ ਲਈ ਵਿਆਜ ਦੀ ਮਾਤਰਾ ਲੱਭਣ ਲਈ IPMT ਫੰਕਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਿਵੇਂ ਕਰੀਏ। ਭੁਗਤਾਨ ਦੀ ਬਾਰੰਬਾਰਤਾ, ਅਤੇ ਕਿਵੇਂ ਕਰਜ਼ੇ ਦੀਆਂ ਸਥਿਤੀਆਂ ਨੂੰ ਬਦਲਣਾ ਸੰਭਾਵੀ ਵਿਆਜ ਨੂੰ ਬਦਲਦਾ ਹੈ।
ਇਸ ਤੋਂ ਪਹਿਲਾਂ ਕਿ ਅਸੀਂ ਇਸ ਵਿੱਚ ਡੁਬਕੀ ਕਰੀਏ, ਇਹ ਨੋਟ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਪੀਐਮਟੀ ਫੰਕਸ਼ਨ ਤੋਂ ਬਾਅਦ ਆਈਪੀਐਮਟੀ ਫਾਰਮੂਲੇ ਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਸਭ ਤੋਂ ਵਧੀਆ ਹੈ ਜੋ ਸਮੇਂ ਦੀ ਕੁੱਲ ਰਕਮ ਦੀ ਗਣਨਾ ਕਰਦਾ ਹੈ ਭੁਗਤਾਨ (ਵਿਆਜ + ਮੂਲ)।
ਵੱਖ-ਵੱਖ ਭੁਗਤਾਨ ਫ੍ਰੀਕੁਐਂਸੀਜ਼ (ਹਫ਼ਤੇ, ਮਹੀਨੇ, ਤਿਮਾਹੀ) ਲਈ IPMT ਫਾਰਮੂਲਾ
ਕਰਜ਼ੇ ਦੇ ਭੁਗਤਾਨ ਦੇ ਵਿਆਜ ਵਾਲੇ ਹਿੱਸੇ ਨੂੰ ਸਹੀ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ, ਤੁਹਾਨੂੰ ਹਮੇਸ਼ਾ ਸਾਲਾਨਾ ਵਿਆਜ ਨੂੰ ਬਦਲਣਾ ਚਾਹੀਦਾ ਹੈ। ਸੰਬੰਧਿਤ ਮਿਆਦ ਦੀ ਦਰ ਅਤੇ ਭੁਗਤਾਨ ਦੀ ਕੁੱਲ ਸੰਖਿਆ ਲਈ ਸਾਲਾਂ ਦੀ ਸੰਖਿਆ ਦੀ ਦਰਪੀਰੀਅਡਜ਼:
- ਦਰ ਦਲੀਲ ਲਈ, ਸਾਲਾਨਾ ਵਿਆਜ ਦਰ ਨੂੰ ਪ੍ਰਤੀ ਸਾਲ ਭੁਗਤਾਨਾਂ ਦੀ ਸੰਖਿਆ ਨਾਲ ਵੰਡੋ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਬਾਅਦ ਵਾਲੀ ਮਿਆਦ ਪ੍ਰਤੀ ਸਾਲ ਮਿਸ਼ਰਿਤ ਮਿਆਦਾਂ ਦੀ ਸੰਖਿਆ ਦੇ ਬਰਾਬਰ ਹੈ।
- nper ਆਰਗੂਮੈਂਟ ਲਈ, ਸਾਲਾਂ ਦੀ ਸੰਖਿਆ ਨੂੰ ਪ੍ਰਤੀ ਸਾਲ ਭੁਗਤਾਨਾਂ ਦੀ ਸੰਖਿਆ ਨਾਲ ਗੁਣਾ ਕਰੋ।
ਹੇਠ ਦਿੱਤੀ ਸਾਰਣੀ ਗਣਨਾਵਾਂ ਦਿਖਾਉਂਦੀ ਹੈ:
| ਭੁਗਤਾਨ ਦੀ ਬਾਰੰਬਾਰਤਾ | ਦਰ ਦੀ ਦਲੀਲ | ਪ੍ਰਤੀ ਦਲੀਲ |
| ਹਫਤਾਵਾਰੀ | ਸਲਾਨਾ ਵਿਆਜ ਦਰ / 52 | ਸਾਲ * 52 |
| ਮਾਸਿਕ | ਸਲਾਨਾ ਵਿਆਜ ਦਰ / 12 | ਸਾਲ * 12 |
| ਤਿਮਾਹੀ | ਸਾਲਾਨਾ ਵਿਆਜ ਦਰ / 4 | ਸਾਲ * 4 |
| ਅਰਧ-ਸਾਲਾਨਾ | ਸਾਲਾਨਾ ਵਿਆਜ ਦਰ / 2 | ਸਾਲ * 2 |
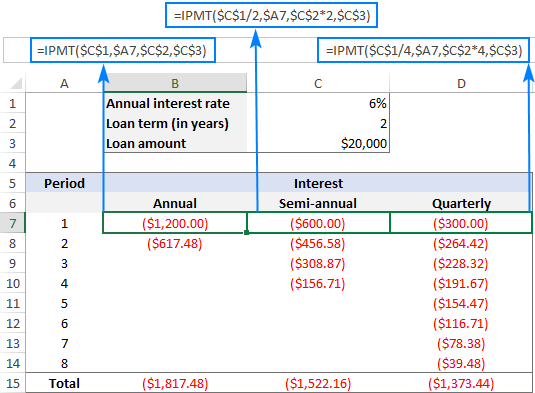
ਉਦਾਹਰਣ ਦੇ ਤੌਰ 'ਤੇ, ਆਓ ਅਸੀਂ ਉਸ ਵਿਆਜ ਦੀ ਰਕਮ ਲੱਭੀਏ ਜੋ ਤੁਹਾਨੂੰ ਉਸੇ ਕਰਜ਼ੇ 'ਤੇ ਅਦਾ ਕਰਨੀ ਪਵੇਗੀ ਪਰ ਵੱਖ-ਵੱਖ ਰੂਪਾਂ ਵਿੱਚ ਭੁਗਤਾਨ ਦੀ ਬਾਰੰਬਾਰਤਾ:
- ਸਲਾਨਾ ਵਿਆਜ ਦਰ: 6%
- ਲੋਨ ਦੀ ਮਿਆਦ: 2 ਸਾਲ
- ਲੋਨ ਦੀ ਰਕਮ: $20,000
- ਅਵਧੀ: 1<11
ਬਾਅਦ ਵਿੱਚ ਬਕਾਇਆ r ਆਖਰੀ ਭੁਗਤਾਨ $0 ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ( fv ਦਲੀਲ ਛੱਡ ਦਿੱਤੀ ਗਈ ਹੈ), ਅਤੇ ਭੁਗਤਾਨ ਹਰੇਕ ਮਿਆਦ ਦੇ ਅੰਤ 'ਤੇ ਬਕਾਇਆ ਹਨ ( ਕਿਸਮ ਦਲੀਲ ਛੱਡੀ ਗਈ ਹੈ)।
ਹਫ਼ਤਾਵਾਰ :
=IPMT(6%/52, 1, 2*52, 20000)
ਮਾਸਿਕ :
=IPMT(6%/12, 1, 2*12, 20000)
ਤਿਮਾਹੀ :
=IPMT(6%/4, 1, 2*4, 20000)
ਅਰਧ-ਸਾਲਾਨਾ :
=IPMT(6%/2, 1, 2*2, 20000)
ਹੇਠਾਂ ਦਿੱਤੇ ਸਕ੍ਰੀਨਸ਼ੌਟ ਨੂੰ ਦੇਖਦੇ ਹੋਏ, ਤੁਸੀਂ ਦੇਖ ਸਕਦੇ ਹੋ ਕਿ ਵਿਆਜ ਦੀ ਰਕਮ ਹਰ ਅਗਲੀ ਮਿਆਦ ਦੇ ਨਾਲ ਘਟਦਾ ਹੈ। ਇਹ ਹੈਕਿਉਂਕਿ ਕੋਈ ਵੀ ਭੁਗਤਾਨ ਕਰਜ਼ੇ ਦੇ ਮੂਲ ਮੂਲ ਨੂੰ ਘਟਾਉਣ ਵਿੱਚ ਯੋਗਦਾਨ ਪਾਉਂਦਾ ਹੈ, ਅਤੇ ਇਹ ਬਾਕੀ ਬਚੇ ਬਕਾਏ ਨੂੰ ਘਟਾਉਂਦਾ ਹੈ ਜਿਸ 'ਤੇ ਵਿਆਜ ਦੀ ਗਣਨਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ।
ਇਸ ਤੋਂ ਇਲਾਵਾ, ਕਿਰਪਾ ਕਰਕੇ ਧਿਆਨ ਦਿਓ ਕਿ ਉਸੇ ਕਰਜ਼ੇ 'ਤੇ ਭੁਗਤਾਨ ਯੋਗ ਵਿਆਜ ਦੀ ਕੁੱਲ ਰਕਮ ਸਾਲਾਨਾ, ਅਰਧ-ਸਾਲਾਨਾ ਲਈ ਵੱਖਰੀ ਹੈ। ਅਤੇ ਤਿਮਾਹੀ ਕਿਸ਼ਤਾਂ:
IPMT ਫੰਕਸ਼ਨ ਦਾ ਪੂਰਾ ਰੂਪ
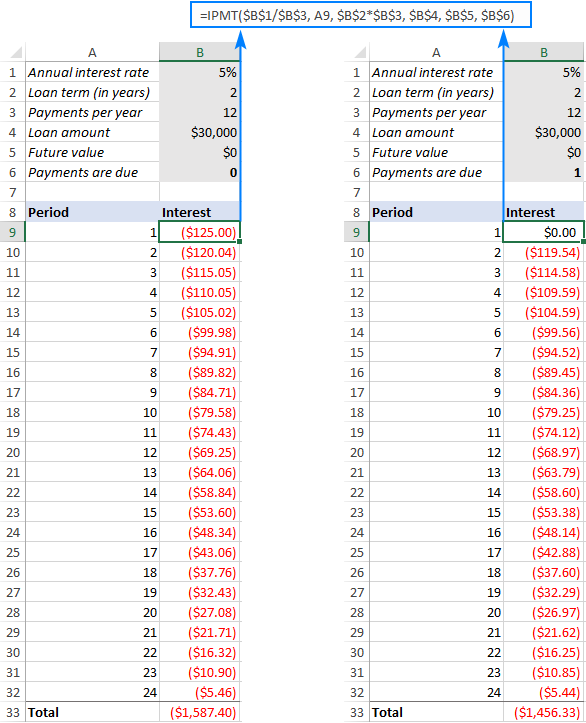
ਇਸ ਉਦਾਹਰਨ ਵਿੱਚ, ਅਸੀਂ ਉਸੇ ਲੋਨ ਲਈ ਵਿਆਜ ਦੀ ਗਣਨਾ ਕਰਨ ਜਾ ਰਹੇ ਹਾਂ, ਉਸੇ ਭੁਗਤਾਨ ਦੀ ਬਾਰੰਬਾਰਤਾ , ਪਰ ਵੱਖ-ਵੱਖ ਸਲਾਨਾ ਕਿਸਮਾਂ (ਰੈਗੂਲਰ ਅਤੇ ਸਲਾਨਾ-ਬਕਾਇਆ)। ਇਸਦੇ ਲਈ, ਸਾਨੂੰ IPMT ਫੰਕਸ਼ਨ ਦੇ ਪੂਰੇ ਰੂਪ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਲੋੜ ਹੋਵੇਗੀ।
ਸ਼ੁਰੂ ਕਰਨ ਲਈ, ਆਓ ਇਨਪੁਟ ਸੈੱਲਾਂ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੀਏ:
- B1 - ਸਾਲਾਨਾ ਵਿਆਜ ਦਰ
- B2 - ਸਾਲਾਂ ਵਿੱਚ ਕਰਜ਼ੇ ਦੀ ਮਿਆਦ
- B3 - ਪ੍ਰਤੀ ਸਾਲ ਭੁਗਤਾਨਾਂ ਦੀ ਗਿਣਤੀ
- B4 - ਕਰਜ਼ੇ ਦੀ ਰਕਮ ( pv )
- B5 - ਭਵਿੱਖ ਦਾ ਮੁੱਲ ( fv )
- B6 - ਜਦੋਂ ਭੁਗਤਾਨ ਬਕਾਇਆ ਹੁੰਦਾ ਹੈ ( ਕਿਸਮ ):
- 0 - ਮਿਆਦ ਦੇ ਅੰਤ 'ਤੇ (ਨਿਯਮਿਤ ਸਾਲਾਨਾ)
- 1 - ਇੱਕ ਪੀਰੀਅਡ ਦੀ ਸ਼ੁਰੂਆਤ ਵਿੱਚ (ਬਕਾਇਆ ਸਾਲਾਨਾ)
ਇਹ ਮੰਨ ਕੇ ਕਿ ਪਹਿਲੀ ਪੀਰੀਅਡ ਨੰਬਰ A9 ਵਿੱਚ ਹੈ, ਸਾਡਾ ਵਿਆਜ ਫਾਰਮੂਲਾ ਇਸ ਤਰ੍ਹਾਂ ਹੈ:
=IPMT($B$1/$B$3, A9, $B$2*$B$3, $B$4, $B$5, $B$6)
ਨੋਟ। ਜੇਕਰ ਤੁਸੀਂ ਇੱਕ ਤੋਂ ਵੱਧ ਸਮੇਂ ਲਈ IPMT ਫਾਰਮੂਲਾ ਵਰਤਣ ਦੀ ਯੋਜਨਾ ਬਣਾ ਰਹੇ ਹੋ, ਤਾਂ ਕਿਰਪਾ ਕਰਕੇ ਸੈੱਲ ਸੰਦਰਭਾਂ 'ਤੇ ਧਿਆਨ ਦਿਓ। ਇਨਪੁਟ ਸੈੱਲਾਂ ਦੇ ਸਾਰੇ ਹਵਾਲੇ ਸੰਪੂਰਨ (ਡਾਲਰ ਚਿੰਨ੍ਹ ਦੇ ਨਾਲ) ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ਤਾਂ ਜੋ ਉਹ ਉਹਨਾਂ ਸੈੱਲਾਂ ਲਈ ਲੌਕ ਹੋ ਜਾਣ। ਪ੍ਰਤੀ ਆਰਗੂਮੈਂਟ ਇੱਕ ਅਨੁਸਾਰੀ ਸੈੱਲ ਸੰਦਰਭ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ (ਬਿਨਾਂ ਡਾਲਰ ਚਿੰਨ੍ਹ ਜਿਵੇਂ ਕਿ A9) ਕਿਉਂਕਿ ਇਹ ਇਸ ਦੇ ਅਧਾਰ ਤੇ ਬਦਲਣਾ ਚਾਹੀਦਾ ਹੈਇੱਕ ਕਤਾਰ ਦੀ ਸਾਪੇਖਿਕ ਸਥਿਤੀ ਜਿਸ ਵਿੱਚ ਫਾਰਮੂਲਾ ਕਾਪੀ ਕੀਤਾ ਗਿਆ ਹੈ।
ਇਸ ਲਈ, ਅਸੀਂ ਉਪਰੋਕਤ ਫਾਰਮੂਲੇ ਨੂੰ B9 ਵਿੱਚ ਦਾਖਲ ਕਰਦੇ ਹਾਂ, ਇਸਨੂੰ ਬਾਕੀ ਦੇ ਪੀਰੀਅਡਾਂ ਲਈ ਹੇਠਾਂ ਖਿੱਚਦੇ ਹਾਂ, ਅਤੇ ਹੇਠਾਂ ਦਿੱਤਾ ਨਤੀਜਾ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ। ਜੇਕਰ ਤੁਸੀਂ ਵਿਆਜ ਕਾਲਮਾਂ (ਖੱਬੇ ਪਾਸੇ ਨਿਯਮਤ ਸਾਲਾਨਾ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਸਾਲਾਨਾ ਬਕਾਇਆ) ਵਿੱਚ ਅੰਕਾਂ ਦੀ ਤੁਲਨਾ ਕਰਦੇ ਹੋ, ਤਾਂ ਤੁਸੀਂ ਵੇਖੋਗੇ ਕਿ ਜਦੋਂ ਤੁਸੀਂ ਮਿਆਦ ਦੀ ਸ਼ੁਰੂਆਤ ਵਿੱਚ ਭੁਗਤਾਨ ਕਰਦੇ ਹੋ ਤਾਂ ਵਿਆਜ ਥੋੜ੍ਹਾ ਘੱਟ ਹੁੰਦਾ ਹੈ।
Excel IPMT ਫੰਕਸ਼ਨ ਕੰਮ ਨਹੀਂ ਕਰ ਰਿਹਾ ਹੈ
ਜੇਕਰ ਤੁਹਾਡਾ IPMT ਫਾਰਮੂਲਾ ਇੱਕ ਗਲਤੀ ਸੁੱਟਦਾ ਹੈ, ਤਾਂ ਇਹ ਇਹਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਹੈ:
- #NUM! ਗਲਤੀ ਹੁੰਦੀ ਹੈ ਪ੍ਰਤੀ ਆਰਗੂਮੈਂਟ ਰੇਂਜ 1 ਤੋਂ nper ਤੋਂ ਬਾਹਰ ਹੈ।
- #VALUE! ਜੇਕਰ ਕੋਈ ਆਰਗੂਮੈਂਟ ਗੈਰ-ਸੰਖਿਆਤਮਕ ਹੈ ਤਾਂ ਗਲਤੀ ਆਉਂਦੀ ਹੈ।
ਇਸ ਤਰ੍ਹਾਂ ਤੁਸੀਂ Excel ਵਿੱਚ IPMT ਫੰਕਸ਼ਨ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋ। ਇਸ ਟਿਊਟੋਰਿਅਲ ਵਿੱਚ ਵਿਚਾਰੇ ਗਏ ਫਾਰਮੂਲਿਆਂ ਨੂੰ ਨੇੜਿਓਂ ਦੇਖਣ ਲਈ, ਸਾਡਾ ਐਕਸਲ IPMT ਫੰਕਸ਼ਨ ਨਮੂਨਾ ਵਰਕਬੁੱਕ ਡਾਊਨਲੋਡ ਕਰਨ ਲਈ ਤੁਹਾਡਾ ਸੁਆਗਤ ਹੈ। ਮੈਂ ਪੜ੍ਹਨ ਲਈ ਤੁਹਾਡਾ ਧੰਨਵਾਦ ਕਰਦਾ ਹਾਂ ਅਤੇ ਅਗਲੇ ਹਫ਼ਤੇ ਤੁਹਾਨੂੰ ਸਾਡੇ ਬਲੌਗ 'ਤੇ ਮਿਲਣ ਦੀ ਉਮੀਦ ਕਰਦਾ ਹਾਂ!

