টিউটোৰিয়েলত দেখুওৱা হৈছে যে ঋণ বা বিনিয়োগৰ বাবে মূলধনৰ ওপৰত পেমেণ্ট গণনা কৰিবলৈ এক্সেলত পিপিএমটি ফাংচন কেনেকৈ ব্যৱহাৰ কৰিব পাৰি।

যেতিয়া আপুনি ঋণ বা বন্ধকত সময়ে সময়ে পেমেণ্ট কৰে, প্ৰতিটো পেমেণ্টৰ এটা নিৰ্দিষ্ট অংশ সুতৰ ফালে যায় (ধাৰ লোৱাৰ বাবে লোৱা মাচুল) আৰু বাকী পেমেণ্ট ঋণৰ মূলধন (আপুনি প্ৰথমে ঋণ লোৱা ধন) পৰিশোধ কৰিবলৈ যায়। সকলো সময়ৰ বাবে মুঠ পেমেণ্টৰ পৰিমাণ স্থিৰ হ'লেও, মূলধন আৰু সুতৰ অংশ বেলেগ বেলেগ - প্ৰতিটো পৰৱৰ্তী পেমেণ্টৰ লগে লগে সুতত কম আৰু মূলধনত অধিক প্ৰয়োগ কৰা হয়।

মাইক্ৰ'চফ্ট এক্সেলৰ দুয়োটাকে বিচাৰি উলিয়াবলৈ বিশেষ কাৰ্য্য আছে মুঠ পেমেণ্টৰ পৰিমাণ আৰু ইয়াৰ অংশসমূহ। এই টিউটোৰিয়েলত আমি প্ৰিন্সিপালৰ ওপৰত পেমেণ্ট গণনা কৰিবলৈ পিপিএমটি ফাংচন কেনেকৈ ব্যৱহাৰ কৰিব লাগে চাম।

এক্সেল পিপিএমটি ফাংচন - বাক্যবিন্যাস আৰু মৌলিক ব্যৱহাৰ

পিপিএমটি এক্সেলৰ ফাংচনে এটা স্থিৰ সুতৰ হাৰ আৰু পেমেণ্ট সূচীৰ ওপৰত ভিত্তি কৰি এটা নিৰ্দিষ্ট সময়ৰ বাবে ঋণ পৰিশোধৰ মূল অংশ গণনা কৰে।

পিপিএমটি ফাংচনৰ বাক্যবিন্যাস তলত দিয়া ধৰণৰ:

ক'ত:

• হাৰ (প্ৰয়োজনীয়) - ঋণৰ বাবে স্থিৰ সুতৰ হাৰ। শতাংশ বা দশমিক সংখ্যা হিচাপে দিব পাৰি।

  উদাহৰণস্বৰূপে, যদি আপুনি ৭ শতাংশ বাৰ্ষিক সুতৰ হাৰৰ সৈতে ঋণ বা বিনিয়োগত বাৰ্ষিক ধন পৰিশোধ কৰে, তেন্তে ৭% বা ০.০৭ যোগান ধৰে। যদি আপুনি মাহেকীয়া কৰেএকেটা ঋণৰ ওপৰত ধন পৰিশোধ কৰা, তাৰ পিছত ৭%/১২ যোগান ধৰা।

• প্ৰতি (প্ৰয়োজনীয়) - লক্ষ্য পেমেণ্টৰ সময়সীমা। ই 1 আৰু nper ৰ মাজৰ এটা পূৰ্ণসংখ্যা হ'ব লাগে।
• Nper (প্ৰয়োজনীয়) - ঋণ বা বিনিয়োগৰ বাবে মুঠ পৰিশোধৰ সংখ্যা।
• Pv (প্ৰয়োজনীয়) - বৰ্তমানৰ মূল্য, অৰ্থাৎ ভৱিষ্যতে দিয়া ধনৰ শৃংখলাৰ মূল্য এতিয়া কিমান। ঋণৰ বৰ্তমান মূল্য হ’ল আপুনি প্ৰথমে ঋণ লোৱা ধনৰাশি।
• Fv (ঐচ্ছিক) - ভৱিষ্যতৰ মূল্য, অৰ্থাৎ শেষৰ ধন পৰিশোধ কৰাৰ পিছত আপুনি লাভ কৰিব বিচৰা বেলেঞ্চ। যদি বাদ দিয়া হয়, তেন্তে ইয়াক শূন্য (0) বুলি ধৰা হয়।
• ধৰণ (ঐচ্ছিক) - ই সূচায় যে কেতিয়া পেমেণ্টৰ সময়সীমা হ'ব:
  • 0 বা বাদ দিয়া হৈছে - পেমেণ্টৰ সময়সীমা প্ৰতিটো সময়ৰ শেষত।
  • 1 - প্ৰতিটো সময়ৰ আৰম্ভণিতে ধন পৰিশোধ কৰিব লাগিব।

উদাহৰণস্বৰূপে, যদি আপুনি 3 বছৰৰ বাবে 50,000 ডলাৰ ঋণ লয় 8% বাৰ্ষিক সুতৰ হাৰৰ সৈতে আৰু আপুনি বাৰ্ষিক ধন পৰিশোধ কৰে, নিম্নলিখিত সূত্ৰই 1 সময়ৰ বাবে ঋণ পৰিশোধৰ মূল অংশ গণনা কৰিব:

=PPMT(8%, 1, 3, 50000)

যদি আপুনি একেটা ঋণতে মাহেকীয়া পেমেণ্ট কৰিব, তাৰ পিছত এই সূত্ৰ ব্যৱহাৰ কৰক:

=PPMT(8%/12, 1, 3*12, 50000)

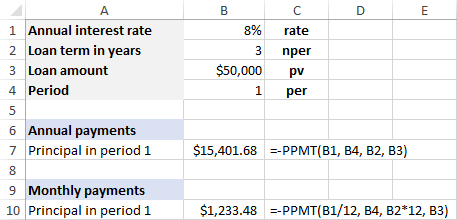
সূত্ৰত থকা যুক্তিসমূহ হাৰ্ডকোড কৰাৰ পৰিৱৰ্তে, আপুনি সিহতক ইনপুট কৰিব পাৰে পূৰ্বনিৰ্ধাৰিত কোষসমূহ আৰু এই পৰ্দাশটত দেখুওৱাৰ দৰে সেই কোষসমূহ চাওক:

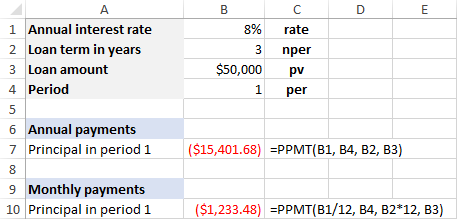
যদি আপুনি ফলাফলটো এটা ধনাত্মক সংখ্যা হিচাপে ল'ব বিচাৰে, তেন্তে a ৰাখক বিয়োগ চিহ্নৰ আগত সমগ্ৰ পিপিএমটি সূত্ৰ বা... pv যুক্তি (ঋণৰ পৰিমাণ)। উদাহৰণস্বৰূপে:

=-PPMT(8%, 1, 3, 50000)

বা

=PPMT(8%, 1, 3, -50000)

এক্সেল পিপিএমটি ফাংচনৰ বিষয়ে আপুনি জানিবলগীয়া ৩টা কথা

আপোনাৰ কাৰ্য্যপত্ৰিকাত PPMT সূত্ৰসমূহ সফলতাৰে ব্যৱহাৰ কৰিবলৈ, অনুগ্ৰহ কৰি নিম্নলিখিত তথ্যসমূহ মনত ৰাখক:

1. মূলধনক এটা ঋণাত্মক নম্বৰ হিচাপে ঘূৰাই দিয়া হয় কাৰণ ই এটা আউটগোয়িং পেমেণ্ট .
2. অবিকল্পিতভাৱে, ফলাফলত মুদ্ৰা বিন্যাস প্ৰয়োগ কৰা হয়, ঋণাত্মক সংখ্যাসমূহ ৰঙা ৰঙেৰে হাইলাইট কৰা আৰু বন্ধনীত আবদ্ধ কৰা।
3. বিভিন্ন পেমেণ্টৰ বাবে মূল ধন গণনা কৰাৰ সময়ত কম্পাঙ্কসমূহ, নিশ্চিত কৰক যে আপুনি হাৰ আৰু nper যুক্তিসমূহৰ সৈতে সামঞ্জস্যপূৰ্ণ। হাৰ ৰ বাবে বাৰ্ষিক সুতৰ হাৰক প্ৰতি বছৰে দিয়া ধনৰ সংখ্যাৰে ভাগ কৰক (ধৰি লওক ই প্ৰতি বছৰে কম্পাউণ্ডিং পিৰিয়ডৰ সংখ্যাৰ সমান)। nper ৰ বাবে, বছৰৰ সংখ্যাক প্ৰতি বছৰে দিয়া পেমেণ্টৰ সংখ্যাৰে গুণ কৰক।
   • সপ্তাহ : হাৰ - বাৰ্ষিক সুতৰ হাৰ/52; nper - বছৰ*৫২<১১><৮><৯>মাহ<১০>: হাৰ - বাৰ্ষিক সুতৰ হাৰ/১২; nper - বছৰ*12
   • ত্ৰিমাসিক : হাৰ - বাৰ্ষিক সুতৰ হাৰ/4; nper - years*4

এক্সেলত পিপিএমটি সূত্ৰ ব্যৱহাৰ কৰাৰ উদাহৰণ

আৰু এতিয়া, পিপিএমটি কেনেকৈ ব্যৱহাৰ কৰিব লাগে দেখুৱাই দিয়া দুটামান সূত্ৰৰ উদাহৰণ লওঁ উদাহৰণ 1. পিপিএমটি সূত্ৰৰ চমু ৰূপ

ধৰি লওক, আপুনি ঋণৰ বাবে মূলধনৰ ওপৰত পৰিশোধ গণনা কৰিব বিচাৰে। এই উদাহৰণত, সেয়া হ’ব ১২টা মাহিলী পেমেণ্ট,কিন্তু একেটা সূত্ৰই অন্য পেমেণ্ট ফ্ৰিকুৱেন্সিৰ বাবেও কাম কৰিব যেনে সাপ্তাহিক, ত্ৰিমাসিক, অৰ্ধ-বাৰ্ষিক বা বাৰ্ষিক।

আপুনি প্ৰতিটো সময়ৰ বাবে এটা বেলেগ সূত্ৰ লিখাৰ সমস্যাৰ পৰা ৰক্ষা কৰিবলৈ, কিছুমানত পিৰিয়ড সংখ্যা সুমুৱাওক কোষ, কওক A7:A18, আৰু তলত দিয়া ইনপুট কোষসমূহ স্থাপন কৰক:

• B1 - বাৰ্ষিক সুতৰ হাৰ
• B2 - ঋণৰ সময়সীমা (বছৰত)
• B3 - প্ৰতি বছৰে পেমেণ্টৰ সংখ্যা
• B4 - ঋণৰ পৰিমাণ

ইনপুট কোষৰ ওপৰত ভিত্তি কৰি, আপোনাৰ পিপিএমটি সূত্ৰৰ বাবে যুক্তিসমূহ সংজ্ঞায়িত কৰক:

• হাৰ - বাৰ্ষিক সুতৰ হাৰ / প্ৰতি বছৰে পেমেণ্টৰ সংখ্যা ($B$1/$B$3)।
• প্ৰতি - প্ৰথম পেমেণ্টৰ সময়সীমা (A7).
• Nper - বছৰ * প্ৰতি বছৰে পেমেণ্টৰ সংখ্যা ($B$2*$B$3)।
• Pv - ঋণৰ পৰিমাণ ($B$4 )
• Fv - বাদ দিয়া হৈছে, শেষৰ পেমেণ্টৰ পিছত শূন্য বেলেঞ্চ ধৰি লৈ।
• ধৰণ - বাদ দিয়া হৈছে, ধৰি লওক পেমেণ্টসমূহ প্ৰতিটো সময়ৰ অন্তত ত দিব লাগিব।

এতিয়া, সকলো যুক্তি একেলগে ৰাখক আৰু আপুনি নিম্নলিখিত সূত্ৰটো পাব:

=PPMT($B$1/$B$3, A7, $B$2*$B$3, $B$4)

অনুগ্ৰহ কৰি মন কৰক, যে আমি per ৰ বাহিৰে সকলো যুক্তিতে নিৰপেক্ষ কোষ প্ৰসংগ ব্যৱহাৰ কৰো য'ত এটা আপেক্ষিক কোষ প্ৰসংগ (A7) ব্যৱহাৰ কৰা হয়। কাৰণ rate , nper আৰু pv যুক্তিসমূহে ইনপুট কোষসমূহক বুজায় আৰু সূত্ৰটো ক'ত কপি কৰা নহওক কিয়, স্থিৰ হৈ থাকিব লাগে। per যুক্তিটো a ৰ আপেক্ষিক অৱস্থানৰ ওপৰত ভিত্তি কৰি সলনি হ’ব লাগেrow.

C7 ত ওপৰৰ সূত্ৰটো সুমুৱাওক, তাৰ পিছত ইয়াক প্ৰয়োজন অনুসৰি যিমানবোৰ ঘৰলৈ তললৈ টানি নিয়ক, আৰু আপুনি নিম্নলিখিত ফলাফল পাব:

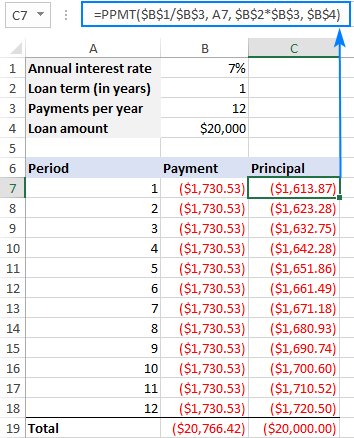
যেনেকৈ আপুনি ওপৰৰ স্ক্ৰীণশ্বটত দেখিব পাৰে, মুঠ পেমেণ্ট (পিএমটি ফাংচনৰ সৈতে গণনা কৰা) সকলো সময়ৰ বাবে একে যেতিয়া মূলধন অংশ প্ৰতিটো একেৰাহে সময়ৰ লগে লগে বৃদ্ধি পায় কাৰণ প্ৰথমতে মূলধনতকৈ অধিক সুত প্ৰদান কৰা হয়।

To PPMT ফাংচনৰ ফলাফল পৰীক্ষা কৰক, আপুনি SUM ফাংচন ব্যৱহাৰ কৰি সকলো মূলধন পৰিশোধ যোগ কৰিব পাৰে, আৰু চাব পাৰে যে যোগফলটো মূল ঋণৰ পৰিমাণৰ সমান নেকি, যিটো আমাৰ ক্ষেত্ৰত $20,000।

উদাহৰণ 2. সম্পূৰ্ণ এই উদাহৰণৰ বাবে, আমি এটা বিনিয়োগ $0 ৰ পৰা আপুনি নিৰ্দিষ্ট কৰা পৰিমাণলৈ বৃদ্ধি কৰিবলৈ প্ৰয়োজনীয় মূলধনৰ ওপৰত পেমেণ্ট গণনা কৰিবলৈ PPMT ফাংচন ব্যৱহাৰ কৰিম।

যিহেতু আমি গৈ আছো পিপিএমটি ফাংচনৰ সম্পূৰ্ণ ৰূপ ব্যৱহাৰ কৰিবলৈ আমি অধিক ইনপুট কোষ সংজ্ঞায়িত কৰোঁ:

• B1 - বাৰ্ষিক সুতৰ হাৰ
• B2 - বছৰত বিনিয়োগৰ সময়সীমা
• B3 - পেমেণ্টৰ সংখ্যা প্ৰতি বছৰ
• B4 - বৰ্তমানৰ মান ( pv )
• B5 - ভৱিষ্যতৰ মান ( fv )
• B6 - কেতিয়া পৰিশোধৰ সময়সীমা ( ধৰণ )

পূৰ্বৰ উদাহৰণৰ দৰেই, হাৰৰ বাবে, আমি বাৰ্ষিক সুতৰ হাৰক প্ৰতি বছৰে ধন পৰিশোধৰ সংখ্যাৰে ভাগ কৰোঁ ($B$1/$B$3)। nper ৰ বাবে আমি বছৰৰ সংখ্যাক প্ৰতি বছৰে দিয়া পেমেণ্টৰ সংখ্যাৰে গুণ কৰোঁ ($B$2*$B$3)।

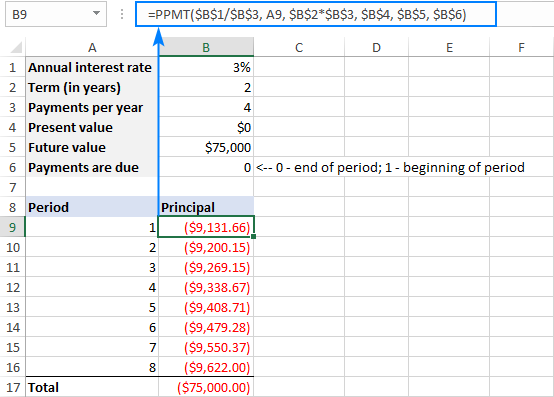
প্ৰথমটোৰ সৈতেA10 ত থকা পেমেণ্ট পিৰিয়ড নম্বৰত, সূত্ৰটোৱে তলত দিয়া আকৃতি লয়:

=PPMT($B$1/$B$3, A10, $B$2*$B$3, $B$4, $B$5, $B$7)

এই উদাহৰণত, পেমেণ্টসমূহ প্ৰতিটো ত্ৰৈমাসিকৰ শেষত 2 বছৰৰ সময়ছোৱাত কৰা হয়। অনুগ্ৰহ কৰি মন কৰক যে সকলো মূলধন পৰিশোধৰ যোগফল বিনিয়োগৰ ভৱিষ্যত মূল্যৰ সমান:

এক্সেল পিপিএমটি ফাংচনে কাম কৰা নাই

যদি এটা পিপিএমটি সূত্ৰই কাম কৰা নাই আপোনাৰ কাৰ্য্যপত্ৰিকাত সঠিকভাৱে, এই সমস্যা সমাধান টিপছসমূহে সহায় কৰিব পাৰে:

1. per যুক্তি 0 তকৈ ডাঙৰ হব লাগে কিন্তু nper তকৈ কম বা সমান হব লাগে, অন্যথা a #NUM! ভুল হয়।
2. সকলো যুক্তি সংখ্যাগত হ'ব লাগে, অন্যথা এটা #VALUE!
3. সাপ্তাহিক, মাহেকীয়া বা ত্ৰিমাসিক পেমেণ্ট গণনা কৰাৰ সময়ত, ওপৰৰ উদাহৰণসমূহত দেখুওৱাৰ দৰে এটা বাৰ্ষিক সুতৰ হাৰক সংশ্লিষ্ট সময়ৰ হাৰলৈ ৰূপান্তৰ কৰাটো নিশ্চিত কৰক, অন্যথা আপোনাৰ পিপিএমটি সূত্ৰৰ ফলাফল ভুল হ'ব।

এক্সেলত আপুনি PPMT ফাংচনটো এনেদৰে ব্যৱহাৰ কৰে। কিছু অনুশীলন পাবলৈ, আপুনি আমাৰ পিপিএমটি সূত্ৰৰ উদাহৰণসমূহ ডাউনলোড কৰিবলৈ আদৰণি জনোৱা হৈছে। পঢ়াৰ বাবে ধন্যবাদ আৰু অহা সপ্তাহত আমাৰ ব্লগত লগ পাম বুলি আশা কৰিলোঁ!