ණයක් හෝ ආයෝජනයක් සඳහා මූලික ගෙවීම ගණනය කිරීමට Excel හි PPMT ශ්‍රිතය භාවිතා කරන ආකාරය නිබන්ධනය පෙන්වයි.

ඔබ ණයක් හෝ උකසක් මත වරින් වර ගෙවීම් කරන විට, සෑම ගෙවීමකින්ම යම් කොටසක් පොලී (ණය ගැනීම සඳහා අය කරන ගාස්තුව) වෙත යන අතර ගෙවීමේ ඉතිරි මුදල ණය ප්‍රධානය (ඔබ මුලින් ණයට ගත් මුදල) ​​ගෙවීමට යයි. සියලුම කාලසීමාවන් සඳහා සම්පූර්ණ ගෙවීමේ මුදල නියත වන අතර, මූලික සහ පොලී කොටස් වෙනස් වේ - එක් එක් අනුප්‍රාප්තික ගෙවීම සමඟ පොලී සඳහා අඩුවෙන් යොදනු ලබන අතර මූලික මුදලට වැඩි ප්‍රමාණයක් යොදනු ලැබේ.

Microsoft Excel හට මේ දෙකම සොයා ගැනීමට විශේෂ කාර්යයන් ඇත. සම්පූර්ණ ගෙවීම් ප්රමාණය සහ එහි කොටස්. මෙම නිබන්ධනයේදී, අපි මූලික ගෙවීම ගණනය කිරීමට PPMT ශ්‍රිතය භාවිතා කරන්නේ කෙසේදැයි බලමු.

Excel PPMT ශ්‍රිතය - වාක්‍ය ඛණ්ඩය සහ මූලික භාවිතයන්

PPMT Excel හි කාර්යය නියත පොලී අනුපාතයක් සහ ගෙවීම් කාලසටහනක් මත පදනම්ව දී ඇති කාල සීමාවක් සඳහා ණය ගෙවීමක ප්‍රධාන කොටස ගණනය කරයි.

PPMT ශ්‍රිතයේ වාක්‍ය ඛණ්ඩය පහත පරිදි වේ:

කොතැනද:

• Rate (අවශ්‍යයි) - ණය සඳහා නියත පොලී අනුපාතය. ප්‍රතිශතයක් හෝ දශම සංඛ්‍යාවක් ලෙස සැපයිය හැක.

  උදාහරණයක් ලෙස, ඔබ සියයට 7 ක වාර්ෂික පොලී අනුපාතයක් සමඟ ණයක් හෝ ආයෝජනයක් මත වාර්ෂික ගෙවීම් කරන්නේ නම්, 7% හෝ 0.07 සපයන්න. ඔබ මාසික කරන්නේ නම්එම ණය මත ගෙවීම්, පසුව 7%/12 සැපයීම.

• Per (අවශ්‍යයි) - ඉලක්කගත ගෙවීම් කාලය. එය 1 සහ nper අතර පූර්ණ සංඛ්‍යාවක් විය යුතුය.
• Nper (අවශ්‍යයි) - ණය හෝ ආයෝජනය සඳහා වූ මුළු ගෙවීම් ගණන.
• Pv (අවශ්‍යයි) - වර්තමාන අගය, එනම් අනාගත ගෙවීම් මාලාවක් දැන් කොපමණ වටිනවාද යන්න. ණයක වර්තමාන වටිනාකම යනු ඔබ මුලින් ණයට ගත් මුදලයි.
• Fv (විකල්ප) - අනාගත අගය, එනම් අවසාන ගෙවීමෙන් පසු ඔබ ලබා ගැනීමට බලාපොරොත්තු වන ශේෂය. ඉවත් කර ඇත්නම්, එය ශුන්‍ය (0) ලෙස උපකල්පනය කෙරේ.
• වර්ගය (විකල්ප) - ගෙවීම් නියමිත වේලාව පෙන්නුම් කරයි:
  • 0 හෝ මඟ හැරිය - ගෙවීම් නියමිත වේ. එක් එක් කාලපරිච්ඡේදය අවසානයේ.
  • 1 - එක් එක් කාලපරිච්ඡේදය ආරම්භයේදී ගෙවීම් නියමිත වේ.

උදාහරණයක් ලෙස, ඔබ වසර 3ක් සඳහා ඩොලර් 50,000ක් ණයට ගන්නේ නම් 8% ක වාර්ෂික පොලී අනුපාතයක් සහිතව සහ ඔබ වාර්ෂික ගෙවීම් සිදු කරයි, පහත සූත්‍රය 1 කාල සීමාව සඳහා ණය ගෙවීමක ප්‍රධාන කොටස ගණනය කරනු ඇත:

=PPMT(8%, 1, 3, 50000)

නම් ඔබ එම ණය මතම මාසික ගෙවීම් කිරීමට යන්නේ, පසුව මෙම සූත්‍රය භාවිතා කරන්න:

=PPMT(8%/12, 1, 3*12, 50000)

සූත්‍රයේ ඇති තර්ක දෘඪ කේත කිරීම වෙනුවට, ඔබට ඒවා ඇතුළත් කළ හැක පූර්ව නිශ්චිත කොටු සහ මෙම තිර පිටුවේ පෙන්වා ඇති පරිදි එම සෛල වෙත යොමු වන්න:

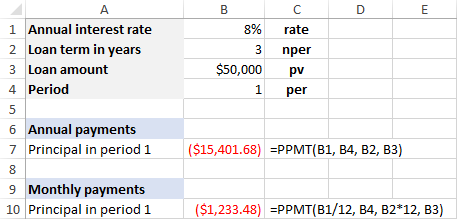
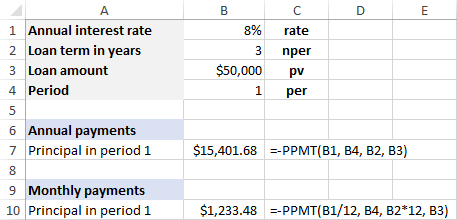
ඔබ ප්‍රතිඵලය ධන අංකයක් ලෙස ලබා ගැනීමට කැමති නම් , ඉන්පසුව සම්පූර්ණ PPMT සූත්‍රයට පෙර අඩු ලකුණ හෝ pv තර්කය (ණය මුදල). උදාහරණයක් ලෙස:

=-PPMT(8%, 1, 3, 50000)

හෝ

=PPMT(8%, 1, 3, -50000)

Excel PPMT ශ්‍රිතය ගැන ඔබ දැනගත යුතු කරුණු 3

ඔබගේ වැඩ පත්‍රිකාවල PPMT සූත්‍ර සාර්ථකව භාවිතා කිරීමට, කරුණාකර පහත කරුණු මතක තබා ගන්න:

1. ප්‍රධාන සෘණ අංකයක් ලෙස ආපසු එවන්නේ එය පිටතට යන ගෙවීමක් වන බැවිනි. .
2. පෙරනිමියෙන්, ප්‍රතිඵලයට මුදල් ආකෘතිය යොදනු ලැබේ, සෘණ අංක රතු පැහැයෙන් උද්දීපනය කර වරහන් තුළ කොට ඇත.
3. විවිධ ගෙවීම් සඳහා ප්‍රධාන මුදල ගණනය කිරීමේදී සංඛ්‍යාත, ඔබ අනුපාතයට සහ nper තර්කවලට අනුකූල බව සහතික කර ගන්න. අනුපාතය සඳහා, වාර්ෂික පොලී අනුපාතිකය වසරකට ගෙවීම් ගණනින් බෙදන්න (එය වසරකට සංයෝජන කාල ගණනට සමාන යැයි උපකල්පනය කරයි). nper සඳහා, වසර ගණන වසරකට ගෙවීම් ගණනින් ගුණ කරන්න.
   • සති : අනුපාතය - වාර්ෂික පොලී අනුපාතය/52; nper - අවුරුදු*52
   • මාස : අනුපාතය - වාර්ෂික පොලී අනුපාතය/12; nper - අවුරුදු*12
   • කාර්තු : අනුපාතය - වාර්ෂික පොලී අනුපාතය/4; nper - years*4

Excel හි PPMT සූත්‍රය භාවිතා කිරීමේ උදාහරණ

දැන්, PPMT භාවිතා කරන ආකාරය පෙන්වන සූත්‍ර උදාහරණ කිහිපයක් ගනිමු. Excel හි ක්‍රියාකාරිත්වය.

උදාහරණය 1. PPMT සූත්‍රයේ කෙටි ආකාරය

ඔබට ණයක් සඳහා ප්‍රින්සිපල් මත ගෙවීම් ගණනය කිරීමට අවශ්‍ය වේ. මෙම උදාහරණයේ දී, එය මාසික ගෙවීම් 12 ක් වනු ඇත,නමුත් සතිපතා, ත්‍රෛමාසික, අර්ධ වාර්ෂික හෝ වාර්ෂික වැනි අනෙකුත් ගෙවීම් සංඛ්‍යාත සඳහාද එම සූත්‍රය ක්‍රියා කරයි.

එක් එක් කාල පරිච්ඡේදය සඳහා වෙනස් සූත්‍රයක් ලිවීමේ ගැටලුව ඔබට ඉතිරි කර ගැනීමට, කාල සීමාවන් කිහිපයක් ඇතුළත් කරන්න. සෛල, A7:A18 කියන්න, සහ පහත සඳහන් ආදාන කොටු සකසන්න:

• B1 - වාර්ෂික පොලී අනුපාතය
• B2 - ණය කාලය (වසර තුළ)
• B3 - වසරකට ගෙවීම් ගණන
• B4 - ණය මුදල

ආදාන කොටු මත පදනම්ව, ඔබේ PPMT සූත්‍රය සඳහා තර්ක නිර්වචනය කරන්න:

• අනුපාතය - වාර්ෂික පොලී අනුපාතය / වසරකට ගෙවීම් ගණන ($B$1/$B$3).
• Per - පළමු ගෙවීමේ කාලය (A7).
• Nper - වසර * වසරකට ගෙවීම් ගණන ($B$2*$B$3).
• Pv - ණය මුදල ($B$4) )
• Fv - අවසන් ගෙවීමෙන් පසු ශුන්‍ය ශේෂය යැයි උපකල්පනය කරයි.
• වර්ගය - මඟ හැරිය, උපකල්පනය කරන ගෙවීම් එක් එක් කාලපරිච්ඡේදයේ අවසානය ට නියමිතයි.

දැන්, සියලු තර්ක එකට එකතු කරන්න, එවිට ඔබට පහත සූත්‍රය ලැබෙනු ඇත:

කරුණාකර අවධානය යොමු කරන්න, සාපේක්ෂ සෛල යොමුවක් (A7) භාවිතා කරන per හැර අනෙකුත් සියලුම තර්ක වලදී අපි නිරපේක්ෂ සෛල යොමු භාවිතා කරමු. මෙයට හේතුව අනුපාතය , nper සහ pv තර්ක ආදාන කොටු වෙත යොමු වන අතර සූත්‍රය කොතැනක පිටපත් කළත් නියතව පැවතිය යුතුය. a හි සාපේක්ෂ පිහිටීම මත පදනම්ව per තර්කය වෙනස් විය යුතුයපේළිය.

ඉහත සූත්‍රය C7 හි ඇතුළත් කරන්න, ඉන්පසු එය අවශ්‍ය තරම් සෛල ගණනකට ඇද දමන්න, එවිට ඔබට පහත ප්‍රතිඵලය ලැබෙනු ඇත:

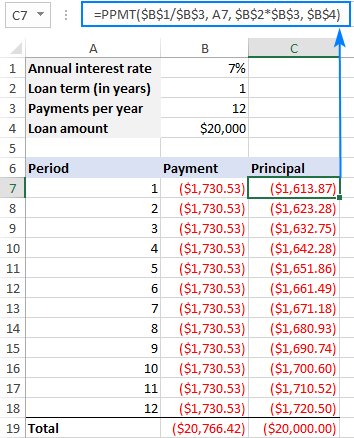
ලෙස ඉහත තිර පිටපතෙහි ඔබට දැක ගත හැක, මුලදී මුලික මුදලට වඩා වැඩි පොලියක් ගෙවන බැවින්, එක් එක් අනුප්‍රාප්තික කාලපරිච්ඡේදය සමඟ ප්‍රධාන කොටස වැඩි වන අතර, සම්පූර්ණ ගෙවීම (PMT ශ්‍රිතය සමඟ ගණනය කරනු ලැබේ) සියලු කාල පරිච්ඡේද සඳහා සමාන වේ.

ට. PPMT ශ්‍රිතයේ ප්‍රතිඵල සත්‍යාපනය කරන්න, ඔබට SUM ශ්‍රිතය භාවිතයෙන් සියලුම ප්‍රධාන ගෙවීම් එකතු කළ හැකි අතර, එම මුදල මුල් ණය මුදලට සමාන වේ දැයි බලන්න, එය අපගේ නඩුවේ $20,000 වේ.

උදාහරණ 2. සම්පූර්ණයි. PPMT සූත්‍රයේ ආකෘතිය

මෙම උදාහරණය සඳහා, අපි $0 සිට ඔබ සඳහන් කරන මුදල දක්වා ආයෝජනයක් වැඩි කිරීමට අවශ්‍ය ප්‍රධාන මත ගෙවීම් ගණනය කිරීමට PPMT ශ්‍රිතය භාවිතා කරන්නෙමු.

අපි යන නිසා PPMT ශ්‍රිතයේ සම්පූර්ණ ස්වරූපය භාවිතා කිරීම සඳහා, අපි තවත් ආදාන කොටු නිර්වචනය කරමු:

• B1 - වාර්ෂික පොලී අනුපාතය
• B2 - වසරවල ආයෝජන වාරය
• B3 - ගෙවීම් සංඛ්යාව වර්ෂය
• B4 - වත්මන් අගය ( pv )
• B5 - අනාගත අගය ( fv )
• B6 - විට ගෙවීම් නියමිතයි ( වර්ගය )

පෙර උදාහරණය සමඟින්, අනුපාතය සඳහා, අපි වාර්ෂික පොලී අනුපාතය වසරකට ගෙවීම් ගණනින් බෙදන්නෙමු ($B$1/$B$3). nper සඳහා, අපි වසර ගණන වසරකට ගෙවීම් ගණනින් ගුණ කරමු ($B$2*$B$3).

පළමු එක සමඟA10 හි ගෙවීම් කාල සීමාව, සූත්‍රය පහත හැඩය ගනී:

=PPMT($B$1/$B$3, A10, $B$2*$B$3, $B$4, $B$5, $B$7)

මෙම උදාහරණයේ දී, වසර 2ක කාලයක් තුළ එක් එක් කාර්තුව අවසානයේ ගෙවීම් කරනු ලැබේ. සියලුම ප්‍රධාන ගෙවීම්වල එකතුව ආයෝජනයේ අනාගත වටිනාකමට සමාන බව කරුණාවෙන් සලකන්න:

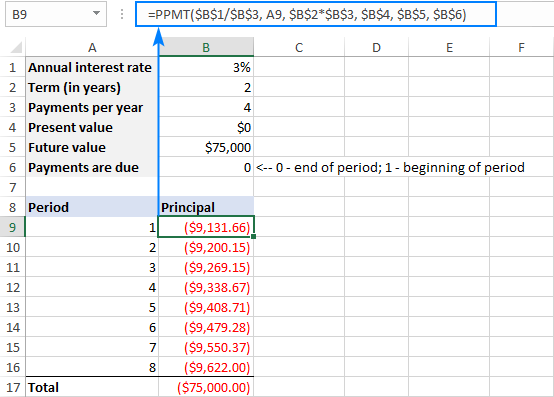
Excel PPMT ශ්‍රිතය ක්‍රියා නොකරයි

PPMT සූත්‍රයක් ක්‍රියා නොකරන්නේ නම් ඔබේ වැඩ පත්‍රිකාවේ නිවැරදිව, මෙම දෝශ නිරාකරණ ඉඟි උදවු විය හැක:

1. per තර්කය 0 ට වඩා වැඩි විය යුතු නමුත් nper ට වඩා අඩු හෝ සමාන විය යුතුය, එසේ නොමැතිනම් a #NUM! දෝෂයක් ඇතිවේ.
2. සියලු තර්ක සංඛ්‍යාත්මක විය යුතුය, එසේ නොමැතිනම් #VALUE! දෝෂයක් ඇතිවේ.
3. සතිපතා, මාසික හෝ ත්‍රෛමාසික ගෙවීම් ගණනය කිරීමේදී, ඉහත උදාහරණවල පෙන්වා ඇති පරිදි වාර්ෂික පොලී අනුපාතයක් අනුරූප කාල සීමාවට පරිවර්තනය කිරීමට වග බලා ගන්න, එසේ නොමැතිනම් ඔබේ PPMT සූත්‍රයේ ප්‍රතිඵලය වැරදි වනු ඇත.

ඔබ Excel හි PPMT ශ්‍රිතය භාවිතා කරන්නේ එලෙසයි. යම් පුහුණුවක් ලබා ගැනීම සඳහා, අපගේ PPMT සූත්‍ර උදාහරණ බාගත කිරීමට ඔබව සාදරයෙන් පිළිගනිමු. කියවීම ගැන මම ඔබට ස්තූතිවන්ත වන අතර ලබන සතියේ අපගේ බ්ලොග් අඩවියෙන් ඔබව දැකීමට බලාපොරොත්තු වෙමි!