Содржина
Упатството објаснува како да додадете и каде да најдете Solver во различни верзии на Excel, од 2016 до 2003 година. Примерите чекор-по-чекор покажуваат како да се користи Excel Solver за да се најдат оптимални решенија за линеарно програмирање и други видови на проблеми.
Сите знаат дека Microsoft Excel содржи многу корисни функции и моќни алатки кои можат да ви заштедат часови на пресметки. Но, дали знаевте дека има и алатка која може да ви помогне да најдете оптимални решенија за проблемите со одлучување?
Во ова упатство, ќе ги покриеме сите суштински аспекти на додатокот Excel Solver и ќе обезбедиме чекор -упатство по чекор за тоа како да го користите најефикасно.
Што е Excel Solver?
Excel Solver припаѓа на посебен сет на наредбите кои честопати се нарекуваат алатки за анализа на What-if. Тој е првенствено наменет за симулација и оптимизација на различни деловни и инженерски модели.
Додатокот за Excel Solver е особено корисен за решавање на проблеми со линеарни програмирање, ака проблеми со линеарна оптимизација, и затоа понекогаш се нарекува линеарен програмски решавач . Освен тоа, може да се справи со мазни нелинеарни и немазни проблеми. Ве молиме погледнете ги алгоритмите на Excel Solver за повеќе детали.
Иако Solver не може да го реши секој можен проблем, тој е навистина корисен кога се справувате со сите видови проблеми со оптимизација каде што треба да ја донесете најдобрата одлука. На пример, можеколичината нарачана од секој клиент (B10:E10) треба да се испорача. Ова се Ограничени ќелии .
Следно што треба да направите е да ја пресметате вкупната количина испорачана од секој магацин (G7:G8) и вкупно примени стоки од секој клиент (B9:E9). Можете да го направите ова со едноставни формули за сума прикажани на сликата од екранот подолу. Исто така, вметнете ја формулата SUMPRODUCT во C12 за да ги пресметате вкупните трошоци за испорака:
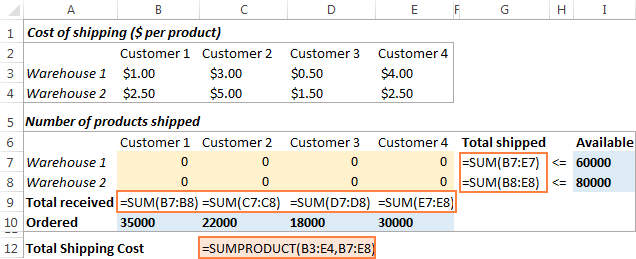
За да го олесните разбирливиот модел за оптимизација на транспортот, креирајте ги следните именувани опсези:
| Име на опсегот | Ќелии | Параметар на решавач |
| Испорачани_производи | B7: E8 | Променливи ќелии |
| Достапни | I7:I8 | Ограничување |
| Вкупно_испратено | G7:G8 | Ограничување |
| Нарачано | B10:E10 | Ограничување |
| Вкупно_примени | B9:E9 | Ограничување |
| Трошоци за испорака | C12 | Цел |
Последното нешто што треба да направите е да ги конфигурирате параметрите на Excel Solver:
- Цел: Shipping_cost поставен на Min
- Променливи ќелии: Производи_испраќани
- Ограничувања: Вкупно_примени = Нарачано и Вкупно_испратено <= Достапно
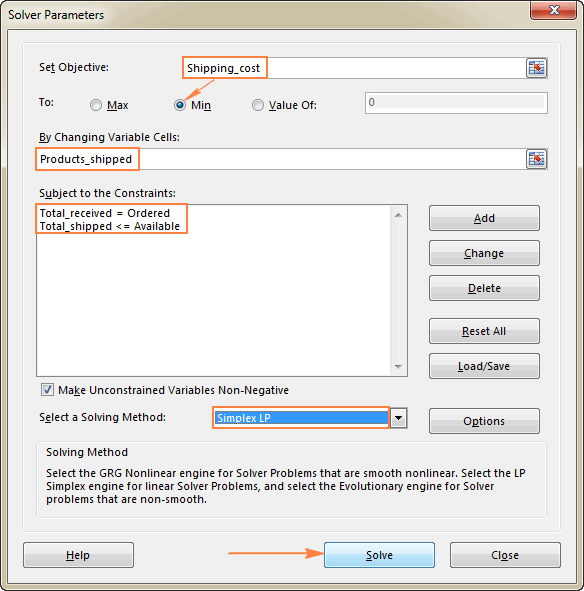
Платете внимание што го избравмеметодот на решавање Simplex LP во овој пример затоа што се занимаваме со проблем со линеарно програмирање. Ако не сте сигурни каков проблем е вашиот, можете да го оставите стандардниот метод за решавање GRG нелинеарно . За повеќе информации, погледнете ги алгоритмите на Excel Solver.
Решение
Кликнете на копчето Реши на дното од прозорецот Параметри на решавачот и вие ќе го добие вашиот одговор. Во овој пример, додатокот Excel Solver ја пресмета оптималната количина на стоки за испорака на секој клиент од секој магацин со минимални вкупни трошоци за испорака:
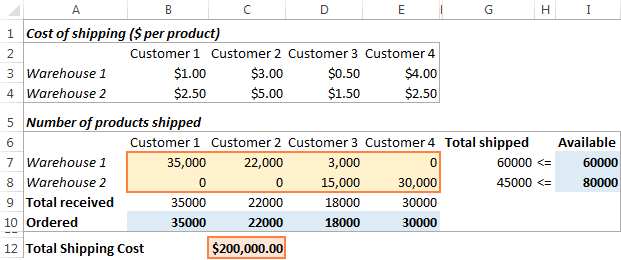
Како да заштедите и вчитајте ги сценаријата на Excel Solver
Кога решавате одреден модел, можеби ќе сакате да ги зачувате вредностите на ќелиите Променливи како сценарио што можете да го прегледате или повторно да го користите подоцна.
На пример, кога се пресметува минималниот трошок за услугата во првиот пример што се дискутира во ова упатство, можеби ќе сакате да пробате различни броеви на проектирани клиенти месечно и да видите како тоа влијае на цената на услугата. Притоа, можеби ќе сакате да го зачувате најверојатното сценарио што веќе сте го пресметале и да го вратите во секој момент.
Зачувување сценариото на Excel Solver се сведува на избор на опсег на ќелии до зачувајте ги податоците внатре. Вчитување моделот Solver е само прашање на обезбедување на Excel со опсегот на ќелии каде што е зачуван вашиот модел. Деталните чекори следат подолу.
Зачувување намодел
За да го зачувате сценариото Excel Solver, направете ги следните чекори:
- Отворете го работниот лист со пресметаниот модел и стартувајте го Excel Solver.
- Во <Прозорец 1>Параметри на решавачот , кликнете на копчето Вчитај/Зачувај .
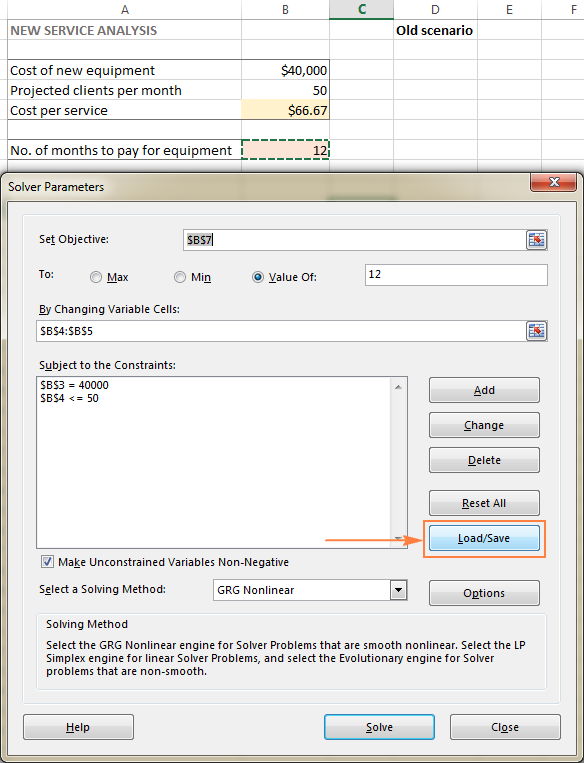
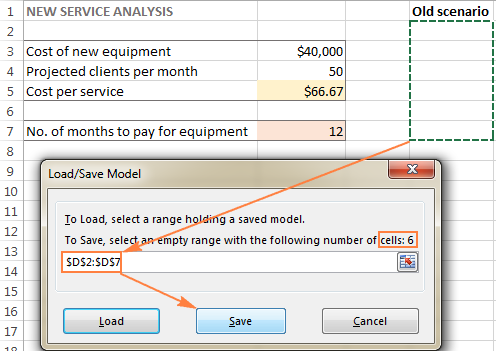
Во исто време, ќе се прикаже прозорецот Параметри на решавачот каде што можете да ги промените вашите ограничувања и да пробате различни опции „што ако“.
Се вчитува зачуваниот модел
Кога ќе одлучите да го вратите зачуваното сценарио, направете го следново:
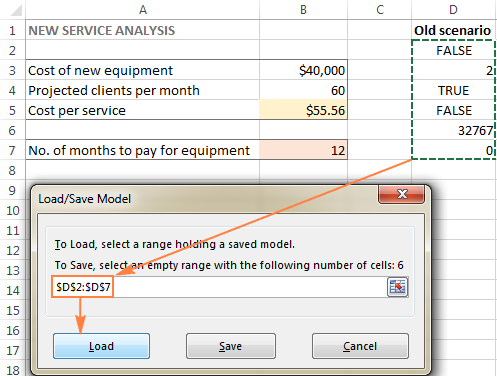
- Во прозорецот Параметри на решавачот , кликнете на Вчитај/ Копче Зачувај .
- На работниот лист, изберете го опсегот на ќелиите што го држат зачуваниот модел и кликнете Вчитај :
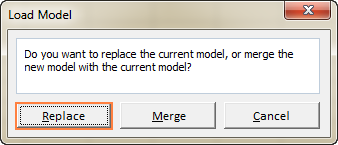
Алгоритми на Excel Solver
Кога дефинирате проблем за Excel Solver, можете да изберете еден од следниве методи во паѓачкото поле Изберете метод за решавање :
- GRG нелинеарно. Генерализиран нелинеарен градиент алгоритам се користи за проблеми кои се мазни нелинеарни, т.е. во кои барем едно од ограничувањата е мазна нелинеарна функција на променливите за одлучување. Повеќе детали можете да најдете овде.
- LP Simplex . Методот Simplex LP Solving се заснова на Симплекс алгоритамот создаден од американскиот математички научник Џорџ Данциг. Се користи за решавање таканаречени проблеми линеарно програмирање - математички модели чии барања се карактеризираат со линеарни врски, односно се состојат од една цел претставена со линеарна равенка која мора да се максимизира или минимизира. За повеќе информации, ве молиме проверете ја оваа страница.
- Evolutionary . Се користи за нерамни проблеми, кои се најтешкиот тип на проблеми за оптимизација за решавање бидејќи некои од функциите се нерамни или дури и прекинати, и затоа е тешко да се одреди насоката во која функцијата се зголемува или намалува. За повеќе информации, погледнете ја оваа страница.
За да промените како Solver наоѓа решение, кликнете на копчето Опции во полето за дијалог Параметри на решавачот и конфигурирајте која било или сите опции на табовите GRG Nonlinear , All Methods и Evolutionary .
Вака можете да го користите Solver во Excel да ги најдете најдобрите решенија за вашите проблеми со одлучување. И сега, можеби ќе сакатепреземете ги примерите на Excel Solver дискутирани во ова упатство и изградете ги обратно за подобро разбирање. Ви благодарам што прочитавте и се надевам дека ќе се видиме на нашиот блог следната недела.
Како да додадете Solver во Excel
Додатокот Solver е вклучен во сите верзии на Microsoft Excel почнувајќи од 2003 година, но тој не е стандардно овозможен.
За да додадете Solver во вашиот Excel, направете ги следните чекори:
- Во Excel 2010 - Excel 365, кликнете Датотека > Опции .
Во Excel 2007, кликнете на копчето Microsoft Office и потоа кликнете Excel Options .
- Во дијалогот Excel Options , кликнете Add-Ins на левата странична лента, проверете 8>Додатоци на Excel се избираат во полето Управување на дното од прозорецот и кликнете Оди .
- Во Додатоци дијалог прозорец, означете го полето Додаток за решавање и кликнете OK :
За да добиете Solver на Excel 2003 , одете во менито Tools и кликнете Add-Ins . Во списокот Додатоци достапни , штиклирајте го полето Додаток за решавање и кликнете OK .
Забелешка. Ако Excel прикаже порака дека додатокот за решавање не е моментално инсталиран на вашиот компјутер, кликнете Да за да го инсталирате.
Каде е Solver во Excel?
Во модерните верзии на Excel, копчето Solver се појавува на табулаторот Податоци , во Анализа група:

Каде еРешавач во Excel 2003?
Откако додатокот Solver ќе се вчита во Excel 2003, неговата команда се додава во менито Tools :
Сега кога знаете каде да го најдете Solver во Excel, отворете нов работен лист и ајде да започнеме!
Забелешка. Примерите дискутирани во ова упатство користат Solver во Excel 2013. Ако имате друга верзија на Excel, сликите од екранот можеби не се совпаѓаат точно со вашата верзија, иако функционалноста на Solver е во основа иста.
Како да го користите Solver во Excel
Пред да го стартувате додатокот Excel Solver, формулирајте го моделот што сакате да го решите во работен лист. Во овој пример, да најдеме решение за следниот едноставен проблем за оптимизација.
Проблем . Да претпоставиме дека сте сопственик на салон за убавина и планирате да обезбедите нова услуга на вашите клиенти. За ова, треба да купите нова опрема која чини 40.000 долари, која треба да се плати на рати во рок од 12 месеци.
Цел : Пресметајте го минималниот трошок по услуга што ќе ви овозможи да платите за новата опрема во наведената временска рамка.
За оваа задача, го создадов следниов модел:
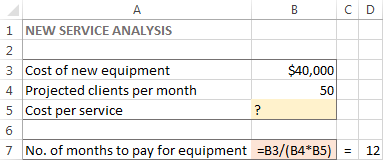
И сега, да видиме како Excel Solver може најдете решение за овој проблем.
1. Стартувај Excel Solver
На табулаторот Податоци , во групата Анализа , кликнете на копчето Решавач .
2. Дефинирајте го проблемот
Прозорецот Параметри на решавачот ќе се отвори каде што иматеза да ги поставите 3-те примарни компоненти:
- Целна ќелија
- Променливи ќелии
- Ограничувања
Токму што прави Excel Solver со горенаведените параметри? Ја наоѓа оптималната вредност (максимална, минимална или одредена) за формулата во ќелијата Цел со менување на вредностите во ќелиите Променлива и предмет на ограничувања во Ограничувања ќелии.
Цел
Ќелијата Цел ( Целна во претходните верзии на Excel) е ќелијата содржи формула што ја претставува целта или целта на проблемот. Целта може да биде максимизирање, минимизирање или постигнување одредена целна вредност.
Во овој пример, целната ќелија е B7, која го пресметува рокот на плаќање користејќи ја формулата =B3/(B4*B5) и резултатот од формулата треба да биде еднаков на 12:
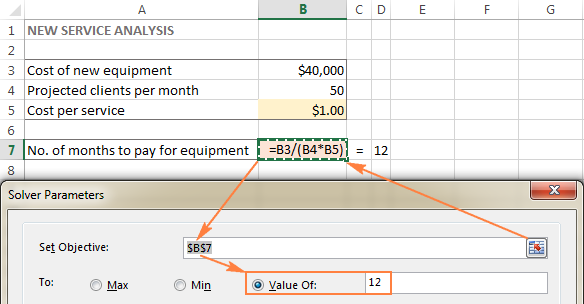
Променливи ќелии
Променливи ќелии ( Промена ќелии или Прилагодливи ќелии во претходните верзии) се ќелии кои содржат променливи податоци кои можат да се променат за да се постигне целта. Excel Solver овозможува одредување до 200 променливи ќелии.
Во овој пример, имаме неколку ќелии чии вредности може да се променат:
- Проектирани клиенти месечно (B4) кои треба да да биде помал или еднаков на 50; и
- Трошоци по услуга (B5) што сакаме да ги пресмета Excel Solver.
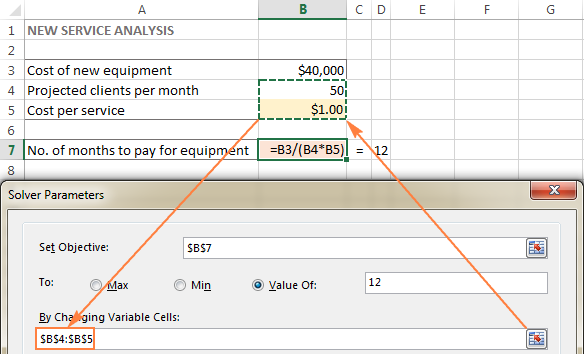
Совет. Ако променливите ќелии или опсези во вашиот модел се несоседни ,изберете ја првата ќелија или опсег, а потоа притиснете и задржете го копчето Ctrl додека избирате други ќелии и/или опсези. Или, рачно напишете ги опсезите, одделени со запирки.
Ограничувања
Решавачот на Excel Ограничувања се ограничувања или ограничувања на можните решенија на проблемот. Поинаку кажано, ограничувањата се условите што мора да се исполнат.
За да додадете ограничувања, направете го следново:
- Кликнете на Додај копче десно до полето „ Предмет на ограничувања “.
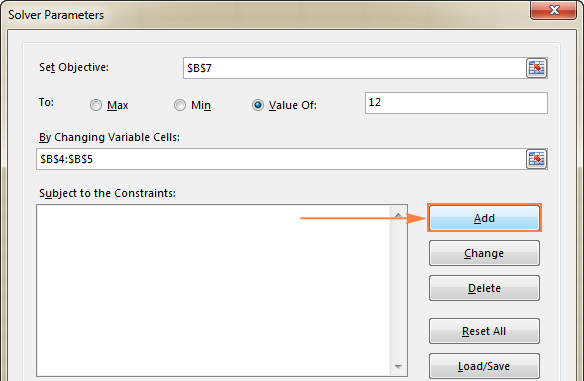
- Во прозорецот Ограничување , внесете ограничување.
- Кликнете на копчето Додај за да го додадете ограничувањето на листата.
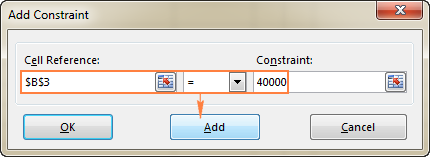
- Продолжи внесување други ограничувања.
- Откако ќе го внесете последното ограничување, кликнете OK за да се вратите во главниот прозорец Решавач Параметри .
Excel Solver овозможува одредување на следните врски помеѓу референцираната ќелија и ограничувањето.
- Помалку или еднакво на , еднакво на , и поголемо или еднакво на . Овие врски ги поставувате со избирање ќелија во полето Референци за ќелии , избирајќи еден од следниве знаци: <= , =, или > ;= , а потоа внесете број, референца / име на ќелија или формула во полето Ограничување (ве молиме погледнете ја горната слика од екранот).
- Цел број . Ако референцираната ќелија мора да биде цел број, изберете int ,а зборот цел број ќе се појави во полето Ограничување .
- Различни вредности . Ако секоја клетка во референтниот опсег мора да содржи различна вредност, изберете dif и зборот AllDifferent ќе се појави во полето Ограничување .
- Бинарно . Ако сакате да ја ограничите референтната ќелија или на 0 или 1, изберете bin и зборот binary ќе се појави во полето Ограничување .
Забелешка. Врските int , bin и dif може да се користат само за ограничувања на ќелиите со променлива.
За уредување или бришење постоечко ограничување, направете го следново:
- Во полето за дијалог Параметри на решавачот , кликнете на ограничување.
- За да го измените избраното ограничување, кликнете Промени и направете ги промените што ги сакате.
- За да го избришете ограничувањето, кликнете на копчето Избриши .
Во овој пример, ограничувањата се:
- B3=40000 - цената на новата опрема е 40.000 $.
- B4<=50 - бројот на проектирани пациенти месечно под 50.
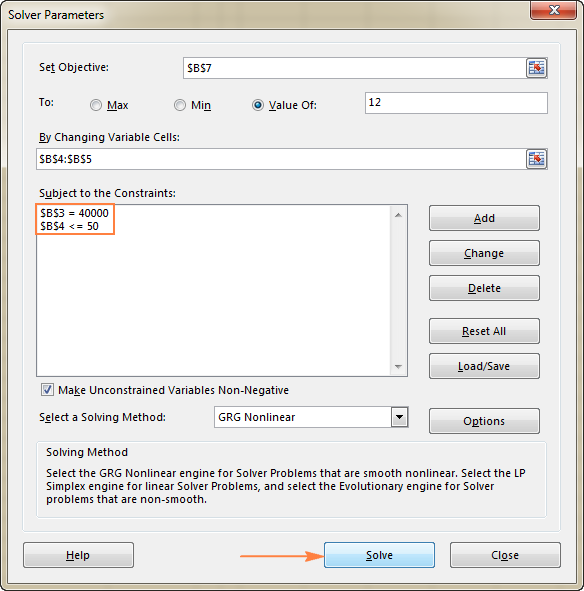
3. Решете го проблемот
Откако ќе ги конфигурирате сите параметри, кликнете на копчето Реши на дното од прозорецот Параметри на решавачот (видете ја сликата од екранот погоре) и оставете додатокот Excel Solver го наоѓа оптималното решение за вашиот проблем.
Во зависност од сложеноста на моделот, компјутерската меморија и брзината на процесорот, може да бидат потребни неколкусекунди, неколку минути, па дури и неколку часа.
Кога Solver ќе заврши со обработката, ќе го прикаже прозорецот за дијалог Резултати за решавање , каде што ќе изберете Задржи го решението за решавање и кликнете OK :
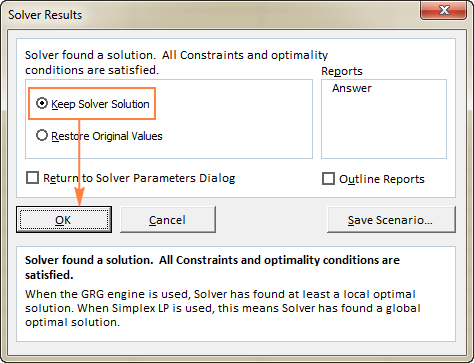
Прозорецот Резултат за решавање ќе се затвори и решението ќе се појави на работниот лист веднаш.
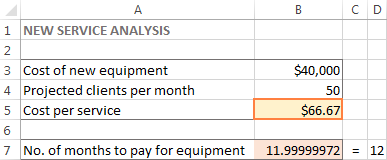
Во овој пример, 66,67 $ се појавуваат во ќелијата B5, што е минималниот трошок по услуга што ќе ви овозможи да платите за новата опрема за 12 месеци, под услов да има најмалку 50 клиенти на месец:
Совети:
- Ако Excel Solver обработува одреден проблем предолго, можете да го прекинете процесот со притискање на Esc клуч. Excel повторно ќе го пресмета работниот лист со последните пронајдени вредности за ќелиите Променлива .
- За да добиете повеќе детали за решениот проблем, кликнете на тип на извештај во полето Извештаи , а потоа кликнете OK . Извештајот ќе биде креиран на нов работен лист:
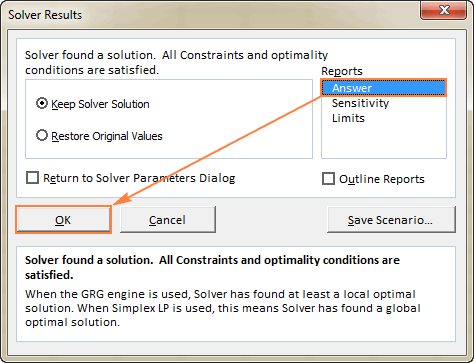
Сега кога ја добивте основната идеја како да користите Solver во Excel, ајде да погледнеме подетално на неколку повеќе примери кои би можеле да ви помогнат да стекнете повеќе разбирање.
Примери на Excel Solver
Подолу ќе најдете уште два примери за користење на додатокот Excel Solver. Прво, ќе најдеме решение за добро позната загатка, а потоа ќе решиме реален проблем со линеарно програмирање.
Excel Solver пример 1 (магичен квадрат)
Iверувајте дека сите се запознаени со загатките „магичен квадрат“ каде што треба да ставите множество броеви на квадрат, така што сите редови, колони и дијагонали се собираат до одреден број.
На пример, дали знаете решение за квадратот 3x3 кој содржи броеви од 1 до 9 каде секоја редица, колона и дијагонала се собираат до 15?
Веројатно не е голема работа да се реши оваа загатка со обиди и грешки, но се обложувам дека Решавачот ќе најде решението побрзо. Нашиот дел од работата е правилно да го дефинираме проблемот.
За почеток, внесете ги броевите од 1 до 9 во табела која се состои од 3 реда и 3 колони. На Excel Solver всушност не му се потребни тие бројки, но тие ќе ни помогнат да го визуелизираме проблемот. Она што навистина му треба на додатокот на Excel Solver се формулите SUM што го вкупуваат секој ред, колона и 2 дијагонали:
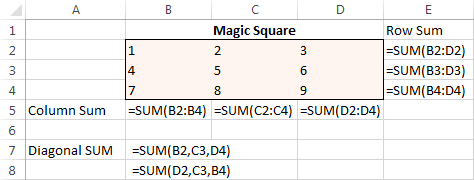
Со сите формули поставени, стартувајте го Solver и поставете следните параметри:
- Постави Цел . Во овој пример, не треба да поставуваме цел, затоа оставете го ова поле празно.
- Променливи ќелии . Сакаме да ги пополниме броевите во ќелиите од B2 до D4, затоа изберете го опсегот B2:D4.
- Ограничувања . Треба да се исполнат следните услови:
- $B$2:$D$4 = AllDifferent - сите ќелии на променливата треба да содржат различни вредности.
- $B$2:$D$4 = цел број - сите од ќелиите на променливата треба да бидат цели броеви.
- $B$5:$D$5 = 15 - збирот на вредностите во секојаколоната треба да изнесува 15.
- $E$2:$E$4 = 15 - збирот на вредностите во секој ред треба да биде 15.
- $B$7:$B$8 = 15 - збирот од двете дијагонали треба да биде еднаква на 15.
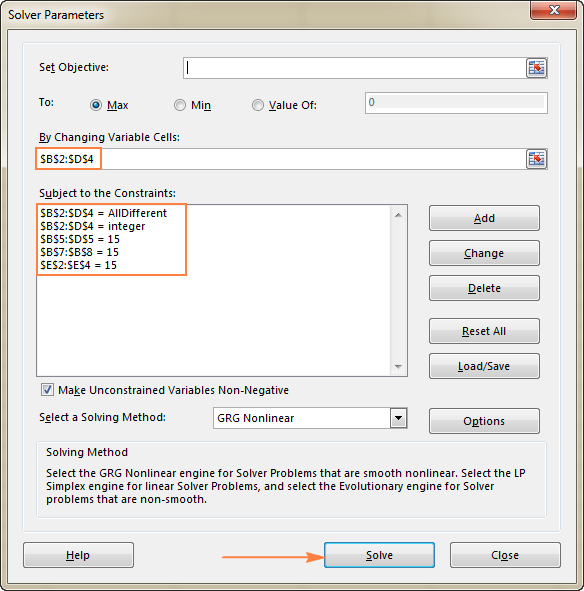
Конечно, кликнете на копчето Реши и решението е таму!
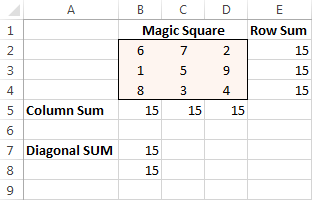
Excel Solver пример 2 (линеарен проблем со програмирање)
Ова е пример за едноставен проблем за оптимизација на транспортот со линеарна цел. Покомплексните модели за оптимизација од овој вид се користат од многу компании за да заштедат илјадници долари секоја година.
Проблем : сакате да ги минимизирате трошоците за испорака на стоки од 2 различни складишта до 4 различни клиенти. Секој магацин има ограничена понуда и секој клиент има одредена побарувачка.
Цел : Минимизирајте ги вкупните трошоци за испорака, не надминувајќи ја количината достапна во секој склад и задоволување на побарувачката на секој клиент .
Изворни податоци
Еве како изгледа нашиот проблем за оптимизација на транспортот:
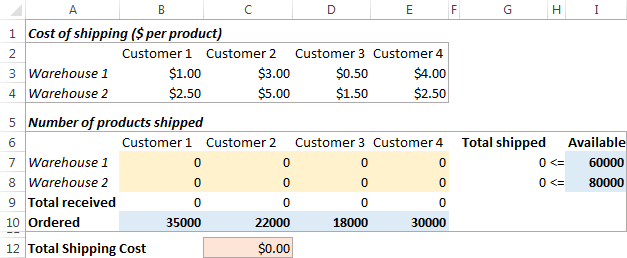
Формулирање на моделот
Да дефинирајте го нашиот линеарен проблем за програмирање за Excel Solver, ајде да одговориме на 3-те главни прашања:
- Кои одлуки треба да се донесат? Сакаме да ја пресметаме оптималната количина на стоки за испорака до секој клиент од секој магацин. Тоа се Променливи ќелии (B7:E8).
- Кои се ограничувањата? Залихите достапни во секој магацин (I7:I8) не може да се надминат, а

