Sisällysluettelo
Ohjeessa selitetään, miten Solver lisätään ja mistä se löytyy eri Excel-versioissa, vuodesta 2016 vuoteen 2003. Vaiheittaiset esimerkit osoittavat, miten Excel Solverin avulla voidaan löytää optimaaliset ratkaisut lineaariseen ohjelmointiin ja muunlaisiin ongelmiin.
Kaikki tietävät, että Microsoft Excel sisältää paljon hyödyllisiä toimintoja ja tehokkaita työkaluja, jotka voivat säästää tuntikausia laskutoimituksia. Mutta tiesitkö, että siinä on myös työkalu, joka voi auttaa sinua löytämään optimaalisia ratkaisuja päätösongelmiin?
Tässä opetusohjelmassa käsittelemme Excel Solver -lisäosan kaikkia olennaisia näkökohtia ja annamme vaiheittaisen oppaan, miten sitä käytetään tehokkaimmin.
Mikä on Excel Solver?
Excel Solver kuuluu erityiseen komentosarjaan, jota kutsutaan usein What-if-analyysityökaluiksi. Se on tarkoitettu ensisijaisesti erilaisten liiketoiminta- ja suunnittelumallien simulointiin ja optimointiin.
Excel Solver -lisäosa on erityisen hyödyllinen lineaaristen ohjelmointiongelmien eli lineaaristen optimointiongelmien ratkaisemisessa, ja siksi sitä kutsutaan toisinaan nimellä lineaarisen ohjelmoinnin ratkaisija Sen lisäksi se pystyy käsittelemään sileitä epälineaarisia ja epäsileviä ongelmia. Katso lisätietoja Excel Solverin algoritmeista.
Vaikka Solver ei pysty ratkaisemaan kaikkia mahdollisia ongelmia, se on todella hyödyllinen kaikenlaisissa optimointiongelmissa, joissa sinun on tehtävä paras mahdollinen päätös. Se voi esimerkiksi auttaa sinua maksimoimaan sijoitetun pääoman tuoton, valitsemaan optimaalisen budjetin mainoskampanjallesi, tekemään parhaan työaikataulun työntekijöillesi, minimoimaan toimituskustannukset ja niin edelleen.
Miten lisätä Solver Exceliin
Solver-lisäohjelma sisältyy kaikkiin Microsoft Excelin versioihin vuodesta 2003 alkaen, mutta se ei ole oletusarvoisesti käytössä.
Voit lisätä Solverin Exceliin suorittamalla seuraavat vaiheet:
- Valitse Excel 2010 - Excel 365:ssä Tiedosto > Vaihtoehdot .
Napsauta Excel 2007:ssä Microsoft Office painiketta ja napsauta sitten Excel-vaihtoehdot .
- Vuonna Excel-vaihtoehdot dialogi, napsauta Lisäosat vasemmassa sivupalkissa, varmista, että Excel-lisäosat on valittu Hallitse laatikko ikkunan alaosassa, ja napsauta sitten Mene .
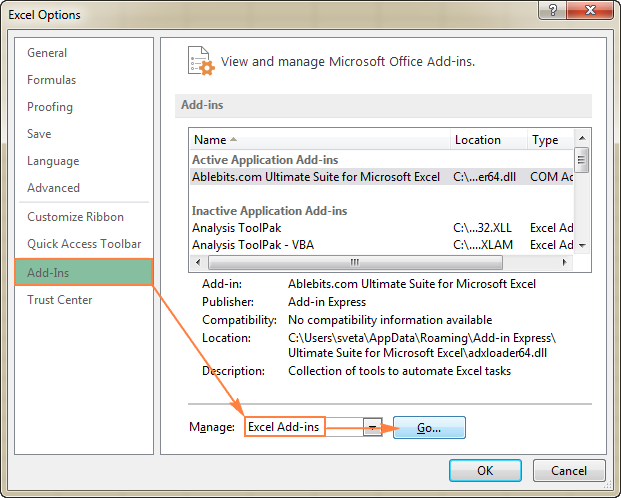
- Vuonna Lisäosat valintaikkunassa, tarkista Solver Add-in ja napsauta OK :
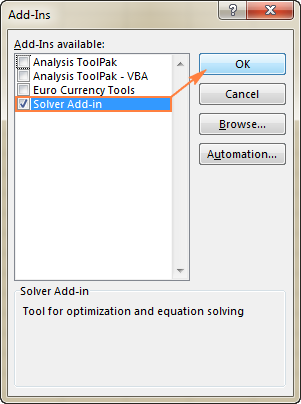
Solverin ottaminen käyttöön Excel 2003 , siirry osoitteeseen Työkalut ja napsauta Lisäosat . Lisäosat saatavilla luettelosta, tarkista Solver Add-in ja napsauta OK .
Huomautus: Jos Excel näyttää viestin, jonka mukaan Solver-lisäohjelmaa ei ole asennettu tietokoneeseen, napsauta kohtaa Kyllä asentaa sen.
Missä on Solver Excelissä?
Nykyaikaisissa Excel-versioissa Ratkaisija painike ilmestyy Tiedot välilehdellä, kohdassa Analyysi ryhmä:

Missä on ratkaisija Excel 2003:ssa?
Kun Solver-lisäohjelma on ladattu Excel 2003:een, sen komento lisätään komentoriviin Työkalut valikko:
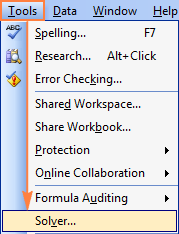
Nyt kun tiedät, mistä löydät Solverin Excelissä, avaa uusi laskentataulukko ja aloitetaan!
Huomautus: Tässä ohjeessa käsitellyissä esimerkeissä käytetään Solveria Excel 2013:ssa. Jos käytössäsi on jokin muu Excel-versio, kuvakaappaukset eivät välttämättä vastaa täysin versiotasi, vaikka Solverin toiminnot ovat periaatteessa samat.
Solverin käyttäminen Excelissä
Ennen Excel Solver -lisäosan käyttämistä muotoile ratkaistava malli työarkissa. Tässä esimerkissä etsitään ratkaisu seuraavaan yksinkertaiseen optimointiongelmaan.
Ongelma Oletetaan, että olet kauneushoitolan omistaja ja suunnittelet tarjoavasi asiakkaillesi uutta palvelua. Tätä varten sinun on ostettava uusi laite, joka maksaa 40 000 dollaria ja joka on maksettava erissä 12 kuukauden kuluessa.
Tavoite : Laske palvelukohtainen vähimmäiskustannus, jonka avulla voit maksaa uuden laitteen tietyn ajan kuluessa.
Tätä tehtävää varten olen luonut seuraavan mallin:
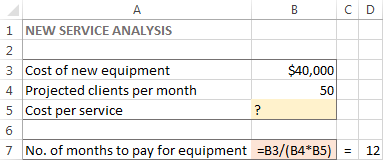
Katsotaan nyt, miten Excel Solver voi löytää ratkaisun tähän ongelmaan.
1. Suorita Excel Solver
On Tiedot välilehdellä, kohdassa Analyysi ryhmää, napsauta Ratkaisija nappi.
2. Määrittele ongelma
The Ratkaisijan parametrit avautuu ikkuna, jossa sinun on määritettävä 3 pääkomponenttia:
- Tavoitesolu
- Muuttuvat solut
- Rajoitukset
Mitä Excel Solver tekee edellä mainituilla parametreilla? Se etsii optimaalisen arvon (maksimi, minimi tai määritetty) kaavan kaavalle kohdassa Tavoite solun muuttamalla arvoja kentässä Muuttuva soluja, ja jollei rajoituksista muuta johdu Rajoitukset soluja.
Tavoite
The Tavoite solu ( Kohde solu aikaisemmissa Excel-versioissa) on solu joka sisältää kaavan Tavoite voi olla maksimointi, minimointi tai jonkin tavoitearvon saavuttaminen.
Tässä esimerkissä tavoitesolu on B7, joka laskee maksuehdon kaavalla =B3/(B4*B5) ja kaavan tuloksen pitäisi olla 12:
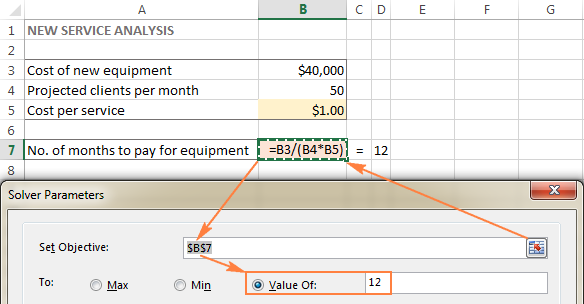
Muuttuvat solut
Muuttuva solut ( Muuttuva soluja tai Säädettävä solut aikaisemmissa versioissa) ovat soluja, jotka sisältävät muuttuvia tietoja, joita voidaan muuttaa tavoitteen saavuttamiseksi. Excel Solver sallii enintään 200 muuttuvan solun määrittämisen.
Tässä esimerkissä on pari solua, joiden arvoja voidaan muuttaa:
- ennakoidut asiakkaat kuukaudessa (B4), joiden määrän tulisi olla enintään 50; ja
- Palvelukohtaiset kustannukset (B5), jotka haluamme Excel Solverin laskevan.
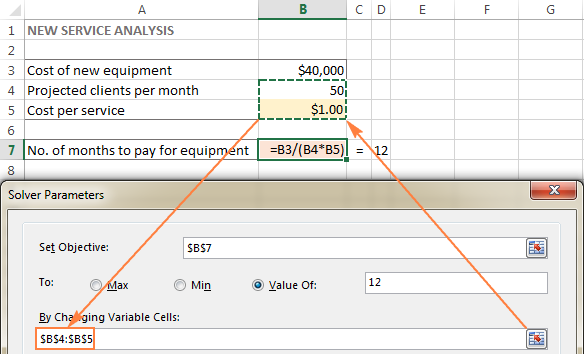
Vihje. Jos mallisi muuttuvat solut tai vaihteluvälit ovat muut kuin vierekkäiset , valitse ensimmäinen solu tai alue ja pidä sitten Ctrl-näppäintä painettuna ja valitse muita soluja ja/tai alueita. Tai kirjoita alueet manuaalisesti pilkulla erotettuina.
Rajoitukset
Excel-ratkaisija Rajoitukset ovat ongelman mahdollisten ratkaisujen rajoituksia tai rajoja. Toisin sanoen rajoitteet ovat ehtoja, joiden on täytyttävä.
Voit lisätä rajoituksen (rajoitukset) seuraavasti:
- Napsauta Lisää painiketta oikealle " Rajoitukset huomioon ottaen " laatikko.
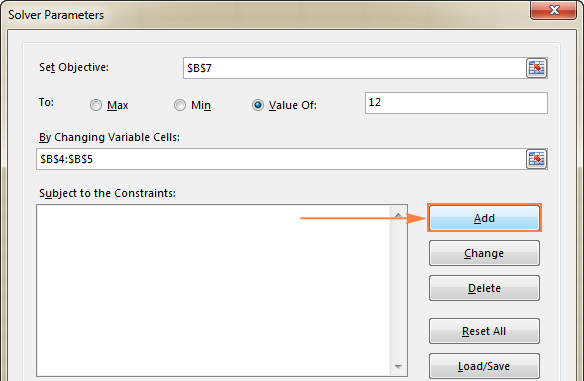
- Vuonna Rajoitus ikkuna, kirjoita rajoitus.
- Napsauta Lisää painiketta lisätäksesi rajoituksen luetteloon.
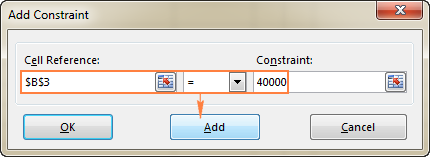
- Jatka muiden rajoitusten syöttämistä.
- Kun olet syöttänyt viimeisen rajoituksen, valitse OK palataksesi pääkuvaan Ratkaisija Parametrit ikkuna.
Excel Solver mahdollistaa seuraavien suhteiden määrittämisen viitattavan solun ja rajoituksen välille.
- Pienempi tai yhtä suuri kuin , yhtä suuri kuin ja suurempi tai yhtä suuri kuin Asetat nämä suhteet valitsemalla solun taulukon Soluviite ruutuun valitsemalla jokin seuraavista merkeistä: <= , =, tai >= ja kirjoita sitten numero, soluviite / solun nimi tai kaava kenttään Rajoitus ruutuun (katso yllä oleva kuvakaappaus).
- Kokonaisluku . Jos viitattavan solun on oltava kokonaisluku, valitse int ja sana kokonaisluku ilmestyy Rajoitus laatikko.
- Eri arvot Jos viitattavan alueen jokaisen solun on sisällettävä eri arvo, valitse dif ja sana AllDifferent ilmestyy Rajoitus laatikko.
- Binäärinen Jos haluat rajoittaa viitattavan solun joko 0:ksi tai 1:ksi, valitse bin ja sana binääri ilmestyy Rajoitus laatikko.
Huomautus. int , bin ja dif suhteita voidaan käyttää vain Variable-solujen rajoituksiin.
Osoitteeseen muokkaa tai poista olemassa olevaa rajoitusta seuraavasti:
- Vuonna Ratkaisijan parametrit valintaikkunassa, napsauta rajoitusta.
- Jos haluat muuttaa valittua rajoitusta, napsauta Muuta ja tee haluamasi muutokset.
- Voit poistaa rajoituksen napsauttamalla Poista nappi.
Tässä esimerkissä rajoitukset ovat:
- B3=40000 - uusien laitteiden kustannukset ovat 40 000 dollaria.
- B4<=50 - alle 50 potilaan ennustettu määrä kuukaudessa.
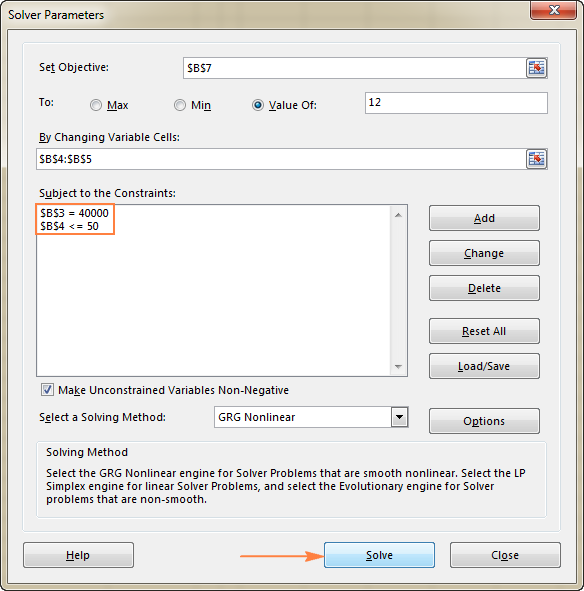
3. Ratkaise ongelma
Kun olet määrittänyt kaikki parametrit, napsauta painiketta Ratkaise painiketta ikkunan alareunassa Ratkaisijan parametrit ikkuna (katso yllä oleva kuvakaappaus) ja anna Excel Solver -lisäosan löytää optimaalinen ratkaisu ongelmaasi.
Mallin monimutkaisuudesta, tietokoneen muistista ja prosessorin nopeudesta riippuen siihen voi kulua muutama sekunti, muutama minuutti tai jopa muutama tunti.
Kun Solver on lopettanut käsittelyn, se näyttää näytön Ratkaisijan tulokset valintaikkuna, jossa valitset Pidä ratkaisija Solution ja klikkaa OK :
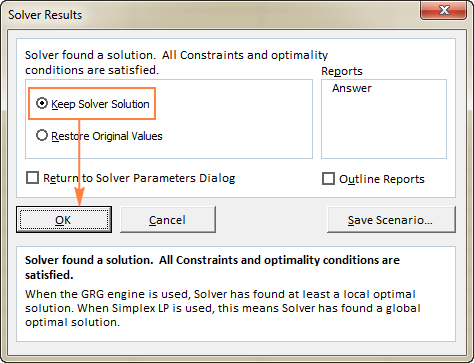
The Ratkaisija Tulos ikkuna sulkeutuu ja ratkaisu ilmestyy heti työarkille.
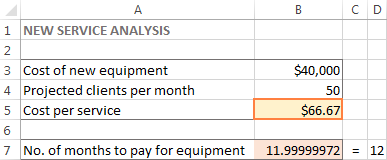
Tässä esimerkissä soluun B5 merkitään 66,67 dollaria, joka on palvelukohtainen vähimmäiskustannus, jolla voit maksaa uuden laitteen 12 kuukaudessa, jos asiakkaita on vähintään 50 kuukaudessa:
Vinkkejä:
- Jos Excel Solver on käsitellyt tiettyä ongelmaa liian kauan, voit keskeyttää prosessin painamalla Esc-näppäintä. Excel laskee laskentataulukon uudelleen viimeisimmillä arvoilla, jotka on löydetty seuraavalle ongelmalle Muuttuva soluja.
- Jos haluat lisätietoja ratkaistusta ongelmasta, napsauta raporttityyppiä kentässä Raportit ja valitse sitten OK Raportti luodaan uudelle työarkille:
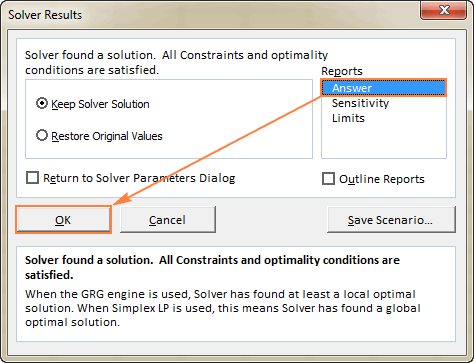
Nyt kun olet saanut perusajatuksen Solverin käytöstä Excelissä, tarkastellaan tarkemmin paria esimerkkiä, jotka voivat auttaa sinua ymmärtämään asiaa paremmin.
Excel Solver esimerkkejä
Alla on kaksi esimerkkiä Excel Solver -lisäosan käytöstä. Ensin etsitään ratkaisu tunnettuun pulmaan ja sitten ratkaistaan todellinen lineaarisen ohjelmoinnin ongelma.
Excel Solver esimerkki 1 (maaginen neliö)
Uskon, että kaikki tuntevat "maagiset neliöt"-arvoitukset, joissa sinun on asetettava joukko numeroita neliöön niin, että kaikki rivit, sarakkeet ja lävistäjät muodostavat tietyn luvun.
Tiedätkö esimerkiksi ratkaisun 3x3-ruutuun, joka sisältää numerot 1-9 ja jossa jokainen rivi, sarake ja lävistäjä on 15?
Tämän pulman ratkaiseminen kokeilemalla ja erehtymällä ei varmaankaan ole iso juttu, mutta lyön vetoa, että Ratkaisija löytää ratkaisun nopeammin. Meidän tehtävämme on määritellä ongelma oikein.
Kirjoita aluksi numerot 1-9 taulukkoon, jossa on 3 riviä ja 3 saraketta. Excel Solver ei oikeastaan tarvitse näitä numeroita, mutta ne auttavat meitä visualisoimaan ongelman. Excel Solver -lisäohjelma tarvitsee oikeastaan SUM-kaavat, jotka laskevat yhteen jokaisen rivin, sarakkeen ja 2 diagonaalia:
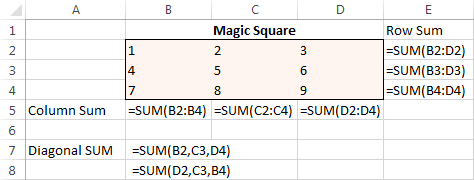
Kun kaikki kaavat ovat valmiina, suorita Solver ja aseta seuraavat parametrit:
- Aseta Tavoite Tässä esimerkissä meidän ei tarvitse asettaa mitään tavoitetta, joten jätä tämä ruutu tyhjäksi.
- Muuttuvat solut Haluamme täyttää solujen B2-D4 numerot, joten valitse alue B2:D4.
- Rajoitukset Seuraavien ehtojen on täytyttävä:
- $B$2:$D$4 = AllDifferent - kaikkien muuttujasolujen tulisi sisältää eri arvoja.
- $B$2:$D$4 = kokonaisluku - kaikkien muuttujasolujen pitäisi olla kokonaislukuja.
- $B$5:$D$5 = 15 - kunkin sarakkeen arvojen summan pitäisi olla 15.
- $E$2:$E$4 = 15 - kunkin rivin arvojen summan pitäisi olla 15.
- $B$7:$B$8 = 15 - molempien lävistäjien summan pitäisi olla 15.
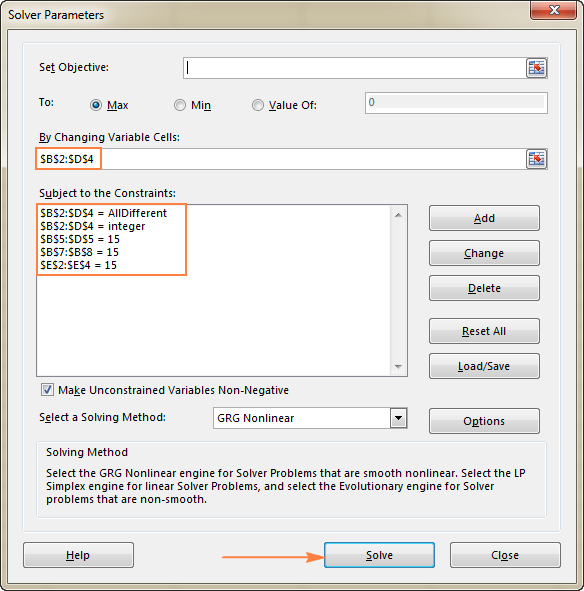
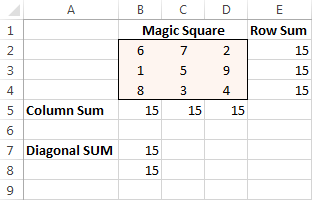
Napsauta lopuksi Ratkaise painiketta, ja ratkaisu on siinä!
Excel Solver esimerkki 2 (lineaarinen ohjelmointiongelma)
Tämä on esimerkki yksinkertaisesta kuljetusten optimointiongelmasta, jolla on lineaarinen tavoite. Monimutkaisempia tämänkaltaisia optimointimalleja käyttävät monet yritykset säästääkseen tuhansia dollareita vuosittain.
Ongelma : Haluat minimoida kustannukset, jotka aiheutuvat tavaroiden lähettämisestä kahdesta eri varastosta neljälle eri asiakkaalle. Kummallakin varastolla on rajallinen tarjonta ja kullakin asiakkaalla on tietty kysyntä.
Tavoite : Minimoi kokonaiskuljetuskustannukset, älä ylitä kussakin varastossa käytettävissä olevaa määrää ja vastaa kunkin asiakkaan kysyntään.
Lähdetiedot
Kuljetusten optimointiongelmamme näyttää seuraavalta:
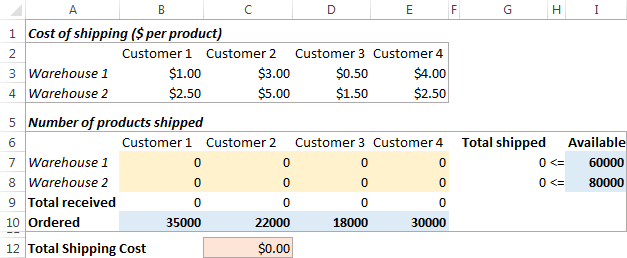
Mallin muotoilu
Jotta voimme määritellä lineaarisen ohjelmoinnin ongelman Excel Solveria varten, vastaamme kolmeen pääkysymykseen:
- Mitä päätöksiä on tehtävä? Haluamme laskea optimaalisen tavaramäärän, joka toimitetaan kullekin asiakkaalle kustakin varastosta. Nämä ovat seuraavat asiat Muuttuva solut (B7:E8).
- Mitkä ovat rajoitteet? Kussakin varastossa (I7:I8) käytettävissä olevia varastoja ei saa ylittää, ja kunkin asiakkaan tilaama määrä (B10:E10) on toimitettava. Nämä ovat seuraavat asiat Rajoitetut solut .
- Mikä on tavoite? - Minimaaliset kokonaiskulut. Ja tämä on meidän... Tavoite solu (C12).
Seuraavaksi sinun on laskettava kustakin varastosta (G7:G8) lähetettyjen tavaroiden kokonaismäärä ja kustakin asiakkaasta vastaanotettujen tavaroiden kokonaismäärä (B9:E9). Voit tehdä tämän yksinkertaisilla Summa-kaavoilla, jotka on esitetty alla olevassa kuvakaappauksessa. Lisää myös SUMPRODUCT-kaava C12-kohtaan, jotta voit laskea toimituskustannukset yhteensä:
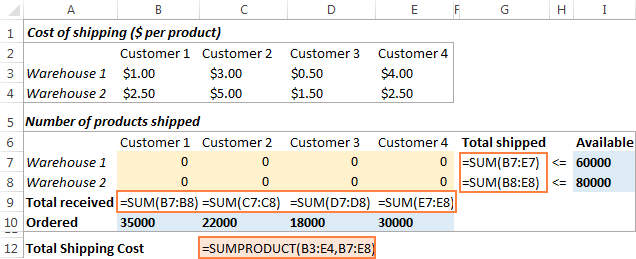
Jotta kuljetusten optimointimallimme olisi helpompi ymmärtää, luo seuraavat nimetyt alueet:
| Alueen nimi | Solut | Ratkaisijan parametri |
| Tuotteet_lähetetty | B7:E8 | Muuttuvat solut |
| Saatavilla | I7:I8 | Rajoitus |
| Total_shipped | G7:G8 | Rajoitus |
| Tilattu | B10:E10 | Rajoitus |
| Yhteensä_vastaanotettu | B9:E9 | Rajoitus |
| Toimituskulut | C12 | Tavoite |
Viimeisenä tehtävänäsi on määrittää Excel Solverin parametrit:
- Tavoite: Shipping_cost on Min
- Muuttujasolut: Products_shipped
- Rajoitukset: Total_received = Tilattu ja Total_shipped <= Saatavilla.
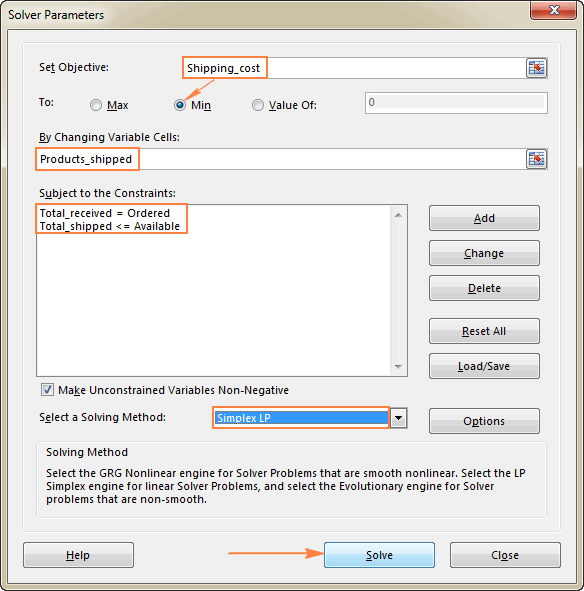
Kiinnitä huomiota siihen, että olemme valinneet Simplex LP ratkaisumenetelmää tässä esimerkissä, koska kyseessä on lineaarinen ohjelmointiongelma. Jos et ole varma, millainen ongelma sinun ongelmasi on, voit jättää oletusarvoisen asetuksen GRG Epälineaarinen Lisätietoja on kohdassa Excel Solver -algoritmit.
Ratkaisu
Napsauta Ratkaise painiketta ikkunan alareunassa Ratkaisijan parametrit Tässä esimerkissä Excel Solver -lisäohjelma laski optimaalisen tavaramäärän, joka voidaan toimittaa kullekin asiakkaalle kustakin varastosta siten, että toimituskustannukset ovat mahdollisimman pienet:
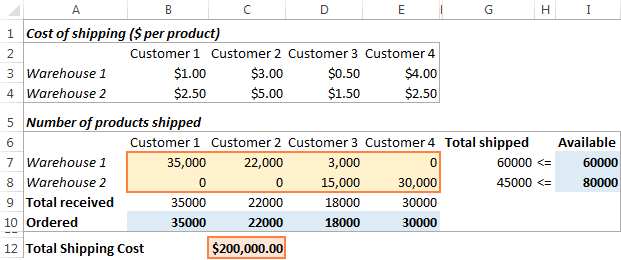
Excel Solver -skenaarioiden tallentaminen ja lataaminen
Kun ratkaiset tiettyä mallia, voit halutessasi tallettaa Muuttuva solujen arvot skenaarioksi, jota voit tarkastella tai käyttää uudelleen myöhemmin.
Kun esimerkiksi lasket minimipalvelukustannuksia aivan ensimmäisessä esimerkissä, jota käsitellään tässä oppaassa, voit kokeilla eri ennustettujen asiakkaiden lukumääriä kuukaudessa ja katsoa, miten se vaikuttaa palvelukustannuksiin. Tällöin voit halutessasi tallentaa jo laskemasi todennäköisimmän skenaarion ja palauttaa sen milloin tahansa.
Säästö Excel Solver -skenaariossa päädytään valitsemaan solualue, johon tiedot tallennetaan. Ladataan Solver-malliin on vain annettava Excelille solualue, johon malli on tallennettu. Seuraavassa on yksityiskohtaiset vaiheet.
Mallin tallentaminen
Voit tallentaa Excel Solver -skenaarion seuraavasti:
- Avaa lasketun mallin sisältävä laskentataulukko ja suorita Excel Solver.
- Vuonna Ratkaisijan parametrit ikkunassa, napsauta Lataa/tallenna nappi.
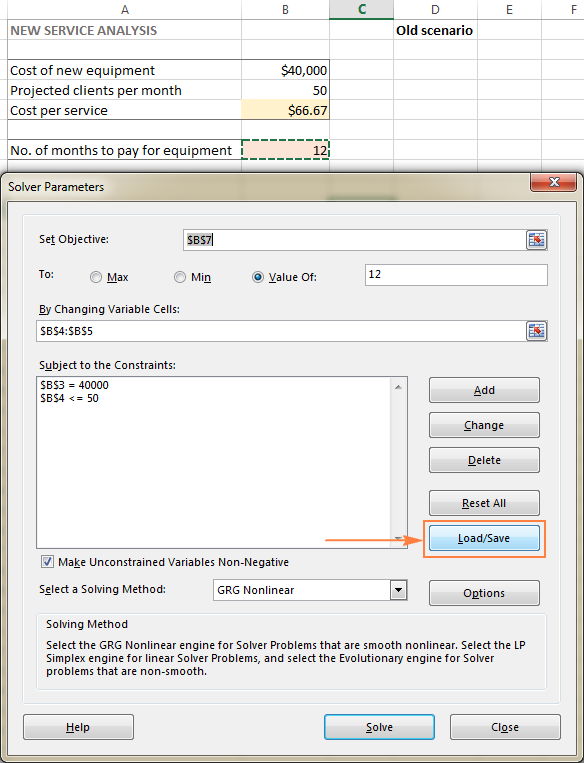
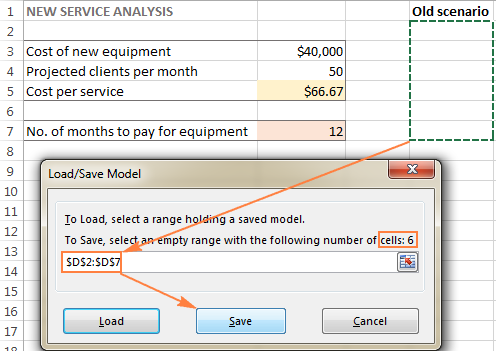
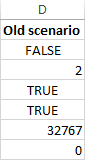
Samaan aikaan Ratkaisijan parametrit avautuu ikkuna, jossa voit muuttaa rajoitteita ja kokeilla erilaisia "mitä jos"-vaihtoehtoja.
Tallennetun mallin lataaminen
Kun päätät palauttaa tallennetun skenaarion, toimi seuraavasti:
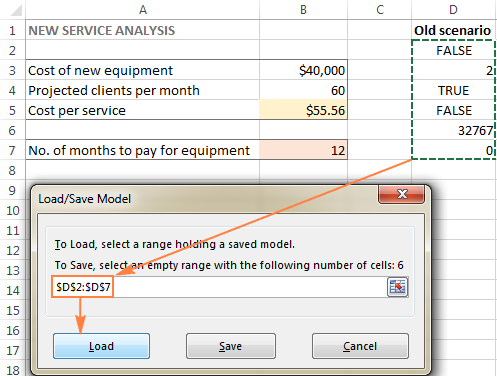
- Vuonna Ratkaisijan parametrit ikkunassa, napsauta Lataa/tallenna nappi.
- Valitse laskentataulukkoon solualue, jossa tallennettu malli on, ja napsauta sitten Lataa :
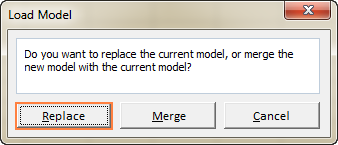
Excel Solver -algoritmit
Kun määrittelet ongelmaa Excel-ratkaisijaa varten, voit valita jonkin seuraavista menetelmistä kentässä Valitse ratkaisumenetelmä pudotusvalikko:
- GRG Nonlinear. Yleistetty vähennetty gradientti Epälineaarinen algoritmia käytetään ongelmiin, jotka ovat sileitä epälineaarisia, eli joissa ainakin yksi rajoituksista on sileä epälineaarinen funktio päätösmuuttujista. Lisätietoja löytyy täältä.
- LP Simplex Simplex LP-ratkaisumenetelmä perustuu yhdysvaltalaisen matemaatikon George Dantzigin luomaan Simplex-algoritmiin. Sitä käytetään ns. Lineaarinen ohjelmointi ongelmat - matemaattiset mallit, joiden vaatimuksia kuvaavat lineaariset suhteet, eli jotka koostuvat yhdestä tavoitteesta, jota edustaa lineaarinen yhtälö, joka on maksimoitava tai minimoitava. Lisätietoja saat tältä sivulta.
- Evoluutio Sitä käytetään ei-sileisiin ongelmiin, jotka ovat vaikeimmin ratkaistavissa olevia optimointiongelmia, koska osa funktioista on epäsileitä tai jopa epäjatkuvia, ja siksi on vaikea määrittää, mihin suuntaan funktio kasvaa tai laskee. Lisätietoja on tällä sivulla.
Jos haluat muuttaa Solverin tapaa löytää ratkaisu, napsauta painiketta Vaihtoehdot painiketta Ratkaisijan parametrit valintaikkunassa ja määrittää minkä tahansa tai kaikki vaihtoehdot kohdassa GRG Epälineaarinen , Kaikki menetelmät ja Evoluutio välilehdet.
Näin voit käyttää Solveria Excelissä löytääksesi parhaat ratkaisut päätöksenteko-ongelmiin. Ja nyt voit ehkä ladata tässä opetusohjelmassa käsitellyt Excel Solver -esimerkit ja kääntää niitä paremman ymmärryksen saamiseksi. Kiitän sinua lukemisesta ja toivon, että näemme sinut blogissamme ensi viikolla.

