Съдържание
В урока е обяснено как да добавите и къде да намерите Solver в различни версии на Excel, от 2016 г. до 2003 г. Примери стъпка по стъпка показват как да използвате Excel Solver за намиране на оптимални решения за линейно програмиране и други видове задачи.
Всеки знае, че Microsoft Excel съдържа много полезни функции и мощни инструменти, които могат да ви спестят часове наред изчисления. Но знаете ли, че в него има и инструмент, който може да ви помогне да намерите оптимални решения за проблеми с решения?
В този урок ще разгледаме всички основни аспекти на добавката Excel Solver и ще ви дадем ръководство стъпка по стъпка как да я използвате най-ефективно.
Какво е Excel Solver?
Решение на Excel принадлежи към специален набор от команди, които често се наричат "Инструменти за анализ на това, което се случи" (What-if Analysis Tools). Той е предназначен предимно за симулация и оптимизация на различни бизнес и инженерни модели.
Добавката Excel Solver е особено полезна за решаване на задачи за линейно програмиране, известни още като задачи за линейна оптимизация, и затова понякога се нарича решаване на линейно програмиране . Освен това той може да се справя с гладки нелинейни и негладки проблеми. За повече подробности вижте алгоритмите на Excel Solver.
Макар че Solver не може да разреши всички възможни проблеми, той е наистина полезен при решаването на всякакви оптимизационни задачи, при които трябва да вземете най-доброто решение. Например той може да ви помогне да увеличите възвръщаемостта на инвестициите, да изберете оптималния бюджет за рекламната си кампания, да съставите най-добрия работен график за служителите си, да сведете до минимум разходите за доставка и т.н.
Как да добавите Solver в Excel
Добавката Solver е включена във всички версии на Microsoft Excel, започвайки от 2003 г., но не е активирана по подразбиране.
За да добавите Solver към вашия Excel, изпълнете следните стъпки:
- В Excel 2010 - Excel 365 щракнете върху Файл > Опции .
В Excel 2007 щракнете върху Microsoft Office и след това щракнете върху Опции на Excel .
- В Опции на Excel кликнете върху Добавки в лявата странична лента, уверете се, че Добавки за Excel е избран в Управление на в долната част на прозореца и щракнете върху Отидете на .
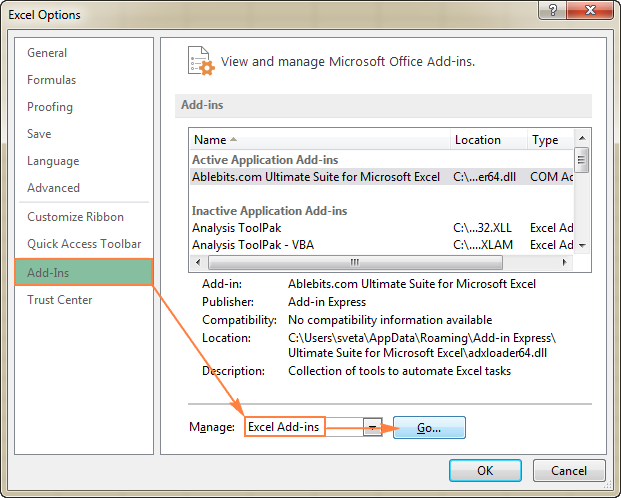
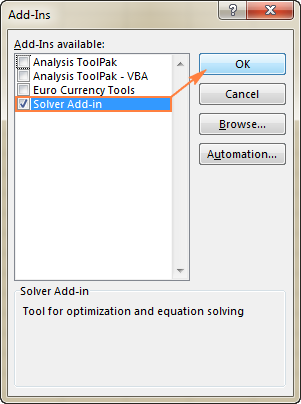
- В Добавки диалогов прозорец, маркирайте Добавка Solver и щракнете върху ОК :
За да включите Solver Excel 2003 , отидете в Инструменти и щракнете върху Добавки . В Добавки на разположение списък, проверете Добавка Solver и щракнете върху ОК .
Забележка: Ако Excel покаже съобщение, че добавката Solver Add-in не е инсталирана на вашия компютър, щракнете върху Да за да го инсталирате.
Къде се намира Solver в Excel?
В съвременните версии на Excel Решаващ орган бутонът се появява на Данни в раздела Анализ група:

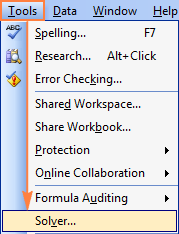
Къде се намира Solver в Excel 2003?
След като добавката Solver бъде заредена в Excel 2003, нейната команда се добавя към Инструменти меню:
Сега, след като знаете къде да намерите Solver в Excel, отворете нов работен лист и нека започнем!
Забележка: Примерите, разгледани в този урок, използват Solver в Excel 2013. Ако имате друга версия на Excel, снимките на екрана може да не съответстват точно на вашата версия, въпреки че функционалността на Solver е основно същата.
Как да използвате Solver в Excel
Преди да стартирате добавката Excel Solver, формулирайте модела, който искате да решите, в работен лист. В този пример нека намерим решение за следната проста оптимизационна задача.
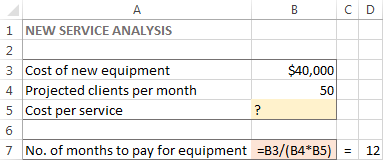
Проблем Да предположим, че сте собственик на салон за красота и планирате да предоставите нова услуга на клиентите си. За целта трябва да закупите ново оборудване, което струва 40 000 USD и което трябва да бъде изплатено на вноски в рамките на 12 месеца.
Цел : Изчислете минималната цена на услуга, която ще ви позволи да платите новото оборудване в рамките на определения срок.
За тази задача създадох следния модел:
А сега нека видим как Excel Solver може да намери решение на този проблем.
1. Стартирайте Excel Solver
На Данни в раздела Анализ щракнете върху групата Решаващ орган бутон.
2. Определяне на проблема
Сайтът Параметри на решаващото устройство Ще се отвори прозорец, в който трябва да настроите трите основни компонента:
- Обективна клетка
- Променливи клетки
- Ограничения
Какво точно прави Excel Solver с горните параметри? Той намира оптималната стойност (максимална, минимална или определена) за формулата в Цел чрез промяна на стойностите в Променлива клетки и при спазване на ограниченията в Ограничения клетки.
Цел
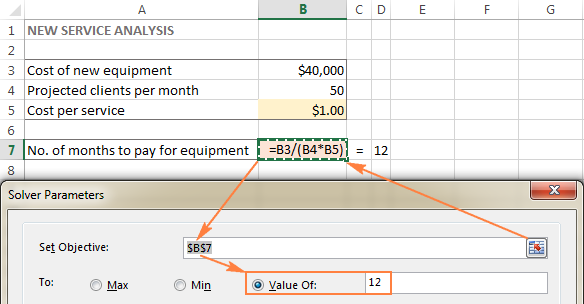
Сайтът Цел клетка ( Цел клетка в по-ранни версии на Excel) е клетката съдържащ формула Целта може да бъде максимизиране, минимизиране или постигане на някаква целева стойност.
В този пример целевата клетка е B7, която изчислява срока на плащане, като използва формулата =B3/(B4*B5) и резултатът от формулата трябва да е равен на 12:
Променливи клетки
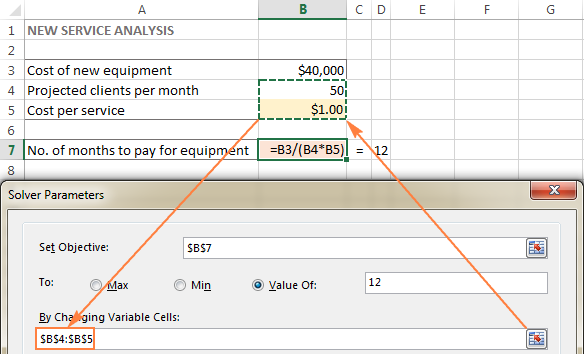
Променлива клетки ( Промяна на клетки или Регулируем клетки в по-ранни версии) са клетки, които съдържат променливи данни, които могат да се променят, за да се постигне целта. Excel Solver позволява задаването на до 200 променливи клетки.
В този пример имаме няколко клетки, чиито стойности могат да се променят:
- Планирани клиенти на месец (B4), които трябва да са по-малко или равни на 50; и
- Разходи за услуга (B5), които искаме да бъдат изчислени от Excel Solver.
Съвет. Ако променливите клетки или диапазони във вашия модел са неприлежащи , изберете първата клетка или диапазон и след това натиснете и задръжте клавиша Ctrl, докато избирате други клетки и/или диапазони. Или въведете диапазоните ръчно, разделени със запетаи.
Ограничения
Решението на Excel Ограничения са ограничения или граници на възможните решения на проблема. Казано по друг начин, ограниченията са условията, които трябва да бъдат изпълнени.
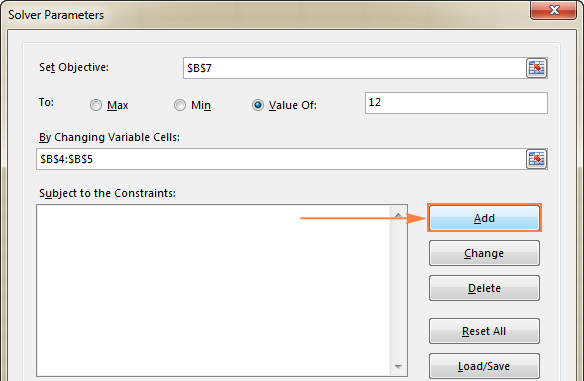
За да добавите ограничение(я), направете следното:
- Щракнете върху Добавяне на бутон вдясно до " При спазване на ограниченията " поле.
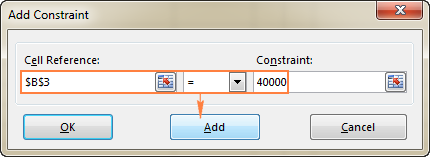
- В Ограничение въведете ограничение.
- Щракнете върху Добавяне на за добавяне на ограничението в списъка.
- Продължете да въвеждате други ограничения.
- След като сте въвели последното ограничение, щракнете върху ОК за да се върнете към главния Решаващ орган Параметри прозорец.
Excel Solver позволява задаването на следните връзки между референтната клетка и ограничението.
- По-малко или равно на , равен на , и по-голям или равен на . Тези връзки се задават, като се избере клетка в Референтна клетка като изберете един от следните знаци: <= , =, или >= и след това въведете число, референция към клетка/име на клетка или формула в Ограничение (моля, вижте горната снимка на екрана).
- Цели числа . Ако препращаната клетка трябва да бъде цяло число, изберете int , а думата цяло число ще се появи в Ограничение кутия.
- Различни стойности . Ако всяка клетка в препратения диапазон трябва да съдържа различна стойност, изберете dif , а думата AllDifferent ще се появи в Ограничение кутия.
- Двоичен . Ако искате да ограничите препратка към клетка до 0 или 1, изберете бин , а думата двоичен ще се появи в Ограничение кутия.
Забележка. int , бин , и dif могат да се използват само за ограничения на клетките с променливи.
За редактиране или изтриване на съществуващо ограничение, направете следното:
- В Параметри на решаващото устройство щракнете върху ограничението в диалоговия прозорец.
- За да промените избраното ограничение, щракнете върху Промяна и направете желаните промени.
- За да изтриете ограничението, щракнете върху Изтриване на бутон.
В този пример ограниченията са:
- B3=40000 - цената на новото оборудване е 40 000 USD.
- B4<=50 - броят на прогнозираните пациенти на месец е под 50.
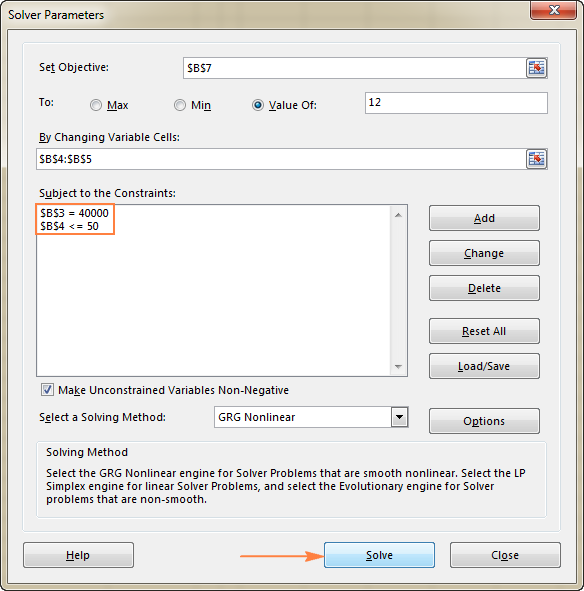
3. Решаване на проблема
След като сте конфигурирали всички параметри, щракнете върху Решаване на проблема бутон в долната част на Параметри на решаващото устройство (вижте снимката на екрана по-горе) и оставете добавката Excel Solver да намери оптималното решение на вашия проблем.
В зависимост от сложността на модела, паметта на компютъра и скоростта на процесора това може да отнеме няколко секунди, няколко минути или дори няколко часа.
Когато Solver завърши обработката, той ще покаже Резултати от решаването диалогов прозорец, в който избирате Запазване на решението за решаване и щракнете върху ОК :
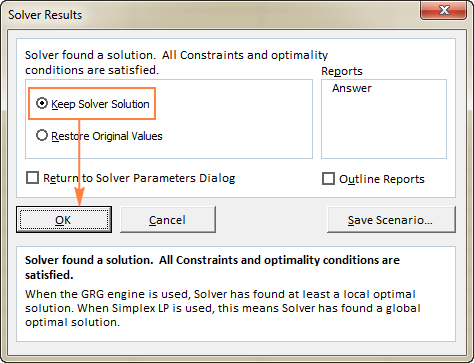
Сайтът Резултат от решаването прозорецът ще се затвори и решението ще се появи веднага в работния лист.
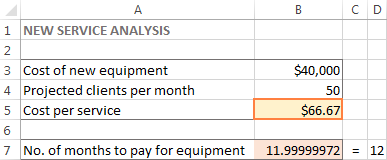
В този пример в клетка В5 се появява 66,67 USD, което е минималната цена на услуга, която ще ви позволи да изплатите новото оборудване за 12 месеца, при условие че има поне 50 клиенти на месец:
Съвети:
- Ако Excel Solver обработва определен проблем твърде дълго, можете да прекъснете процеса, като натиснете клавиша Esc. Excel ще преизчисли работния лист с последните стойности, намерени за Променлива клетки.
- За да получите повече подробности за решената задача, щракнете върху тип отчет в Доклади и след това щракнете върху OK . Отчетът ще бъде създаден в нов работен лист:
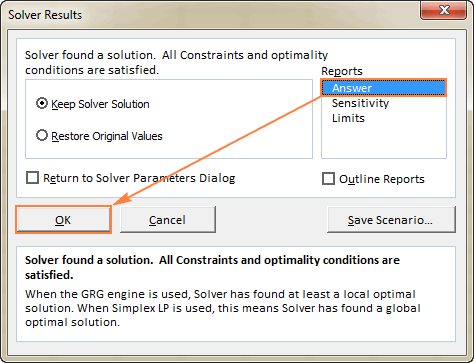
След като вече имате основна представа за това как да използвате Solver в Excel, нека разгледаме по-отблизо още няколко примера, които могат да ви помогнат да ги разберете по-добре.
Примери за решаване на Excel
По-долу ще намерите още два примера за използване на добавката Excel Solver. Първо, ще намерим решение на добре познат пъзел, а след това ще решим реална задача за линейно програмиране.
Пример за решаване на Excel 1 (магически квадрат)
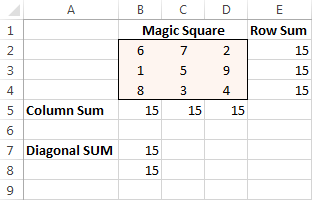
Вярвам, че всеки е запознат с пъзелите "магически квадрат", при които трябва да поставите набор от числа в квадрат, така че всички редове, колони и диагонали да се съберат в определено число.
Знаете ли например решение за квадрата 3х3, съдържащ числата от 1 до 9, в който всеки ред, колона и диагонал дават сбор 15?
Вероятно не е голяма работа да решим този пъзел по метода на пробите и грешките, но се обзалагам, че Solver ще намери решението по-бързо. Нашата част от работата е да определим правилно проблема.
За начало въведете числата от 1 до 9 в таблица, състояща се от 3 реда и 3 колони. Всъщност Excel Solver не се нуждае от тези числа, но те ще ни помогнат да визуализираме проблема. Това, от което добавката Excel Solver наистина се нуждае, са формулите SUM, които сумират всеки ред, колона и 2 диагонала:
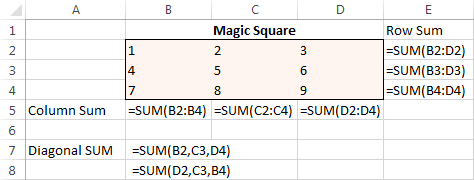
След като всички формули са готови, стартирайте Solver и задайте следните параметри:
- Задайте Цел . В този пример не е необходимо да задаваме цели, затова оставете това поле празно.
- Променливи клетки Искаме да попълним числата в клетките от B2 до D4, затова изберете диапазона B2:D4.
- Ограничения . Трябва да са изпълнени следните условия:
- $B$2:$D$4 = AllDifferent - всички клетки на променливата трябва да съдържат различни стойности.
- $B$2:$D$4 = цяло число - всички клетки от променливата трябва да са цели числа.
- $B$5:$D$5 = 15 - сборът от стойностите във всяка колона трябва да е равен на 15.
- $E$2:$E$4 = 15 - сборът от стойностите във всеки ред трябва да е равен на 15.
- $B$7:$B$8 = 15 - сборът от двата диагонала трябва да е равен на 15.
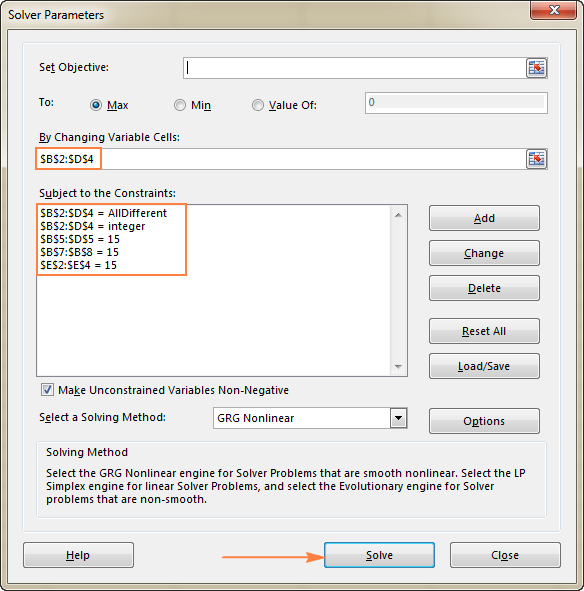
Накрая щракнете върху Решаване на проблема и решението е там!
Пример 2 на Excel Solver (задача за линейно програмиране)
Това е пример за прост проблем за оптимизация на транспорта с линейна цел. По-сложни оптимизационни модели от този вид се използват от много компании, за да спестяват хиляди долари всяка година.
Проблем : Искате да минимизирате разходите за доставка на стоки от 2 различни склада до 4 различни клиенти. Всеки склад има ограничено предлагане, а всеки клиент има определено търсене.
Цел : Минимизиране на общите разходи за доставка, като не се надхвърля наличното количество във всеки склад и се удовлетворява търсенето на всеки клиент.
Източник на данни
Ето как изглежда нашият проблем за оптимизация на транспорта:
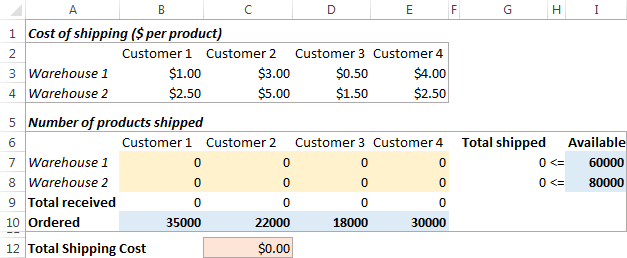
Формулиране на модела
За да определим нашата задача за линейно програмиране за Excel Solver, нека да отговорим на трите основни въпроса:
- Какви решения трябва да се вземат? Искаме да изчислим оптималното количество стоки, които да доставим на всеки клиент от всеки склад. Това са Променлива клетки (B7:E8).
- Какви са ограниченията? Наличните запаси във всеки склад (I7:I8) не могат да бъдат надхвърлени, а поръчаното от всеки клиент количество (B10:E10) трябва да бъде доставено. Това са Ограничен клетки .
- Каква е целта? Минимални общи разходи за доставка. И това е нашата Цел клетка (C12).
Следващото нещо, което трябва да направите, е да изчислите общото количество, изпратено от всеки склад (G7:G8), и общото количество стоки, получени от всеки клиент (B9:E9). Можете да направите това с прости формули Sum, демонстрирани на долната снимка. Също така вмъкнете формулата SUMPRODUCT в C12, за да изчислите общите разходи за доставка:
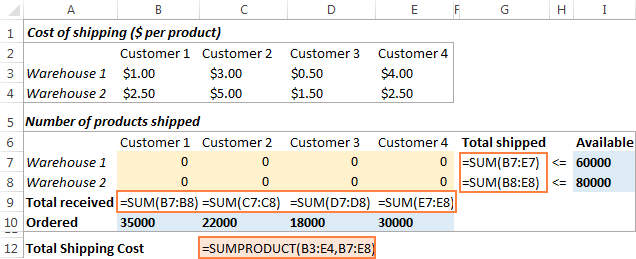
За да направим нашия модел за оптимизация на транспорта по-лесен за разбиране, създайте следните именувани диапазони:
| Име на обхвата | Клетки | Параметър на решаващото устройство |
| Продукти_изпратени | B7:E8 | Променливи клетки |
| Наличен | I7:I8 | Ограничение |
| Общо_изпратени | G7:G8 | Ограничение |
| Поръчано | B10:E10 | Ограничение |
| Общо_получени | B9:E9 | Ограничение |
| Shipping_cost | C12 | Цел |
Последното нещо, което ви остава да направите, е да конфигурирате параметрите на Excel Solver:
- Цел: Shipping_cost се настройва на Min
- Променливи клетки: Products_shipped
- Ограничения: Total_received = поръчано и Total_shipped <= налично
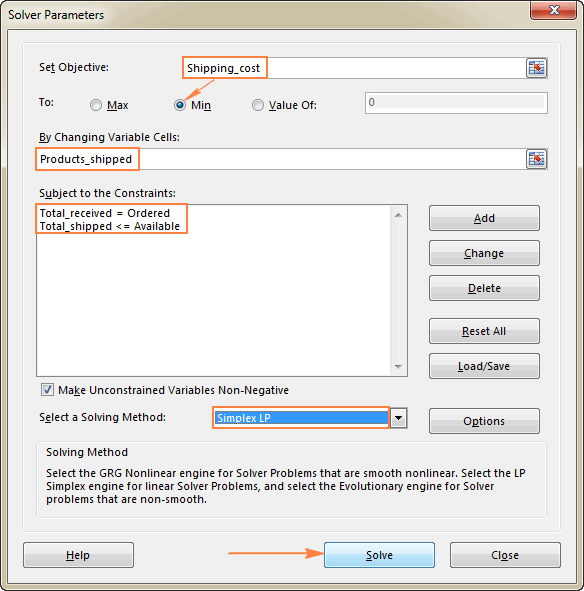
Моля, обърнете внимание, че сме избрали Simplex LP в този пример, тъй като става дума за проблем на линейното програмиране. Ако не сте сигурни какъв е вашият проблем, можете да оставите по подразбиране GRG Нелинейни За повече информация, моля, вижте Алгоритми на Excel Solver.
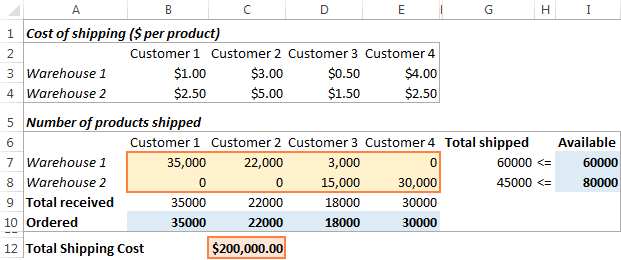
Решение
Щракнете върху Решаване на проблема бутон в долната част на Параметри на решаващото устройство В този пример добавката Excel Solver изчисли оптималното количество стоки за доставка до всеки клиент от всеки склад с минимални общи разходи за доставка:
Как да запазвате и зареждате сценариите на Excel Solver
Когато решавате даден модел, може да искате да запазите Променлива стойности на клетките като сценарий, който можете да прегледате или да използвате отново по-късно.
Например при изчисляването на минималната цена на услугата в първия пример, разгледан в този урок, може да искате да опитате с различен брой прогнозни клиенти на месец и да видите как това се отразява на цената на услугата. При това може да искате да запазите най-вероятния сценарий, който вече сте изчислили, и да го възстановите във всеки един момент.
Спестяване на Сценарият на Excel Solver се свежда до избиране на диапазон от клетки, в които да се запишат данните. Зареждане на модел на Solver е просто въпрос на предоставяне на Excel на обхвата от клетки, където е записан вашият модел. Подробните стъпки следват по-долу.
Запазване на модела
За да запазите сценария на Excel Solver, изпълнете следните стъпки:
- Отворете работния лист с изчисления модел и стартирайте Excel Solver.
- В Параметри на решаващото устройство щракнете върху прозореца Зареждане/запазване бутон.
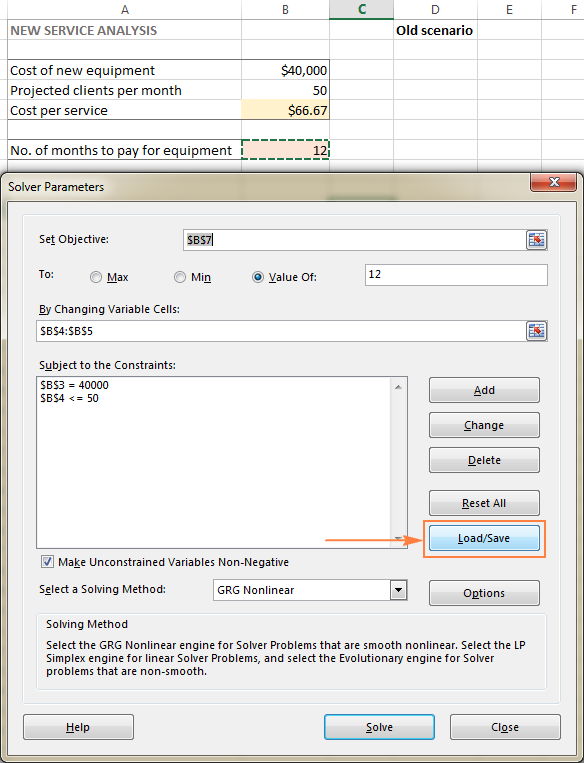
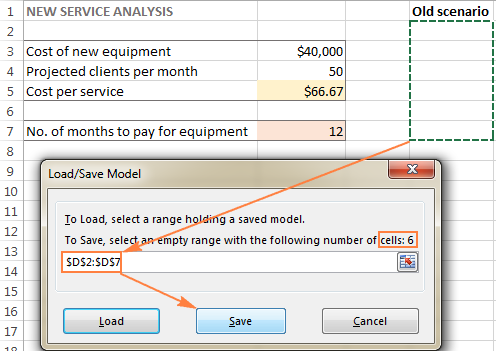
В същото време Параметри на решаващото устройство ще се появи прозорец, в който можете да промените ограниченията и да изпробвате различни варианти "какво ще стане, ако".
Зареждане на запазения модел
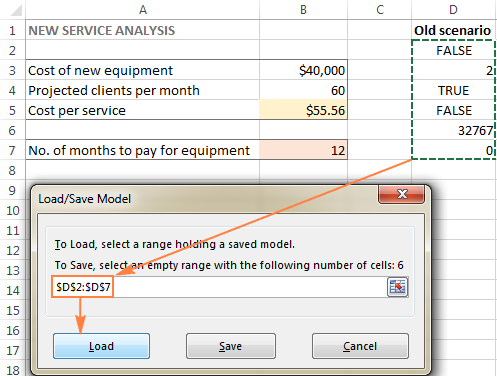
Когато решите да възстановите запазения сценарий, направете следното:
- В Параметри на решаващото устройство щракнете върху прозореца Зареждане/запазване бутон.
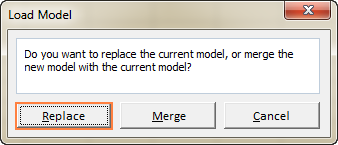
- В работния лист изберете обхвата от клетки, в който се намира запазеният модел, и щракнете върху Зареждане :
Алгоритми на Excel Solver
Когато дефинирате задача за Excel Solver, можете да изберете един от следните методи в Избор на метод за решаване падащо поле:
- GRG Нелинейни. Обобщен намален градиент Нелинейни Алгоритъмът се използва за проблеми, които са гладки нелинейни, т.е. при които поне едно от ограниченията е гладка нелинейна функция на променливите за вземане на решение. повече подробности можете да намерите тук.
- LP Simplex Методът Simplex LP Solving се основава на алгоритъма Simplex, създаден от американския математик Джордж Данциг. Той се използва за решаване на т.нар. Линейно програмиране задачи - математически модели, чиито изисквания се характеризират с линейни зависимости, т.е. състоят се от една цел, представена с линейно уравнение, която трябва да бъде максимизирана или минимизирана. За повече информация, моля, разгледайте тази страница.
- Еволюционен . Той се използва за негладки задачи, които са най-трудният за решаване тип оптимизационни задачи, тъй като някои от функциите са негладки или дори прекъснати и поради това е трудно да се определи посоката, в която дадена функция нараства или намалява. За повече информация вижте тази страница.
За да промените начина, по който Solver намира решение, щракнете върху Опции бутон в Параметри на решаващото устройство и конфигурирайте всички или някои от опциите в диалоговия прозорец GRG Нелинейни , Всички методи , и Еволюционен раздели.
Ето как можете да използвате Solver в Excel, за да намирате най-добрите решения за вашите проблеми с решения. А сега може да изтеглите примерите за Excel Solver, разгледани в този урок, и да ги прегледате за по-добро разбиране. Благодаря ви, че прочетохте, и се надявам да се видим в нашия блог следващата седмица.

