단계별 예제가 포함된 Excel 해 찾기 자습서

Michael Brown

16-05-2023 뛰어나다
  • 이 공유
Michael Brown

이 튜토리얼은 2016년부터 2003년까지 다양한 Excel 버전에서 해 찾기를 추가하는 방법과 찾는 위치를 설명합니다. 단계별 예제에서는 Excel 해 찾기를 사용하여 선형 계획법 및 기타 종류의 작업에 대한 최적의 솔루션을 찾는 방법을 보여줍니다. 문제.

Microsoft Excel에는 계산 시간을 절약할 수 있는 유용한 기능과 강력한 도구가 많이 포함되어 있다는 것을 누구나 알고 있습니다. 그러나 결정 문제에 대한 최적의 솔루션을 찾는 데 도움이 되는 도구도 있다는 것을 알고 계셨습니까?

이 자습서에서는 Excel 해 찾기 추가 기능의 모든 필수 측면을 다루고 단계를 제공합니다. - 가장 효과적으로 사용하는 방법에 대한 단계별 가이드.

    Excel Solver란 무엇입니까?

    Excel Solver 는 What-if 분석 도구라고도 하는 명령. 주로 다양한 비즈니스 및 엔지니어링 모델의 시뮬레이션 및 최적화를 목적으로 합니다.

    Excel Solver 추가 기능은 선형 프로그래밍 문제, 즉 선형 최적화 문제를 해결하는 데 특히 유용하므로 이라고도 합니다. 선형 프로그래밍 솔버 . 그 외에도 부드러운 비선형 및 비매끄러운 문제를 처리할 수 있습니다. 자세한 내용은 Excel Solver 알고리즘을 참조하세요.

    해 찾기가 가능한 모든 문제를 해결할 수는 없지만 최선의 결정을 내려야 하는 모든 종류의 최적화 문제를 처리할 때 정말 유용합니다. 예를 들어,각 고객이 주문한 수량(B10:E10)이 배송되어야 합니다. 이들은 제한된 셀입니다.

  • 목표는 무엇입니까? 배송의 최소 총 비용. 이것이 우리의 목표 셀(C12)입니다.

    • 다음으로 해야 할 일은 각 창고(G7:G8)에서 배송된 총 수량을 계산하는 것입니다. 각 고객이 받은 총 상품(B9:E9). 아래 스크린샷에 나와 있는 간단한 합계 수식을 사용하여 이 작업을 수행할 수 있습니다. 또한 C12에 SUMPRODUCT 공식을 삽입하여 총 배송비를 계산합니다.

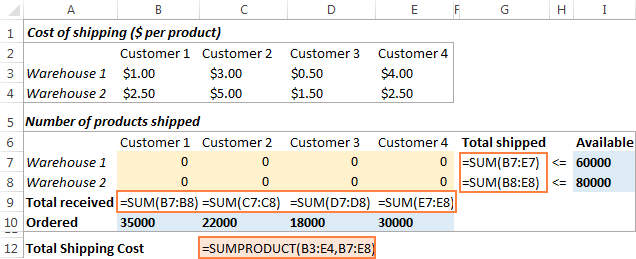
    운송 최적화 모델을 더 쉽게 이해할 수 있도록 다음 명명된 범위를 만듭니다.

    범위 이름 셀 솔버 매개변수
    Products_shipped B7: E8 가변 셀
    사용 가능 I7:I8 제약
    Total_shipped G7:G8 제약
    주문됨 B10:E10 제약
    Total_received B9:E9 Constraint
    Shipping_cost C12 목표

    마지막으로 해야 할 일은 Excel 해 찾기 매개변수를 구성하는 것입니다.

    • 목표: Shipping_cost를 분으로 설정
    • 변수 셀: Products_shipped
    • 제약: Total_received = Ordered 및 Total_shipped <= 사용 가능

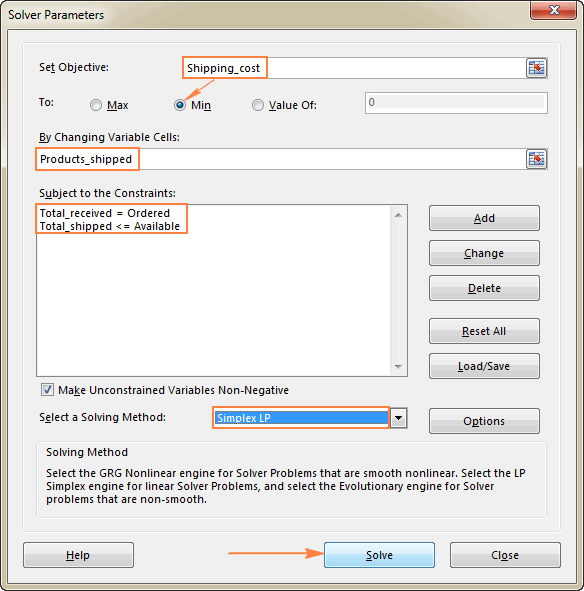
    지불하세요. 우리가 선택한 관심선형 계획법 문제를 다루고 있기 때문에 이 예제에서는 Simplex LP 해결 방법을 사용합니다. 어떤 종류의 문제인지 확실하지 않은 경우 기본 GRG Nonlinear 해결 방법을 그대로 둘 수 있습니다. 자세한 내용은 Excel Solver 알고리즘을 참조하십시오.

    Solution

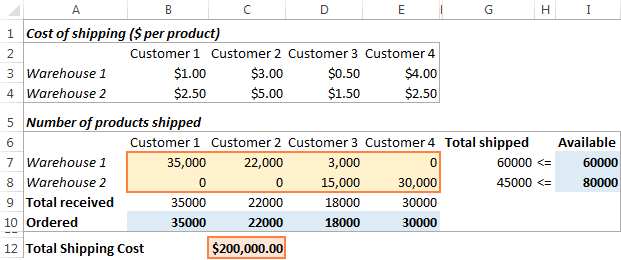
    Solver Parameters 창 하단의 Solve 버튼을 클릭하면 답을 얻을 것입니다. 이 예에서 Excel Solver 추가 기능은 최소 총 배송 비용으로 각 창고에서 각 고객에게 배송할 최적의 상품 수량을 계산했습니다.

    저장 방법 Excel Solver 시나리오 로드

    특정 모델을 해석할 때 변수 셀 값을 나중에 보거나 재사용할 수 있는 시나리오로 저장하고 싶을 수 있습니다.

    예를 들어, 이 튜토리얼에서 논의된 첫 번째 예에서 최소 서비스 비용을 계산할 때 매달 다른 수의 예상 클라이언트를 시도하고 이것이 서비스 비용에 어떤 영향을 미치는지 확인할 수 있습니다. 이때 이미 계산한 가장 가능성 있는 시나리오를 저장하고 언제든지 복원할 수 있습니다. Excel Solver 시나리오

    저장 은 셀 범위를 선택하는 것으로 요약됩니다. 데이터를 저장합니다. Solver 모델을 로드 하는 것은 모델이 저장된 셀 범위를 Excel에 제공하기만 하면 됩니다. 자세한 단계는 다음과 같습니다.

    저장model

    Excel Solver 시나리오를 저장하려면 다음 단계를 수행합니다.

    1. 계산된 모델이 있는 워크시트를 열고 Excel Solver를 실행합니다.
    2. Solver Parameters 창에서 Load/Save 버튼을 클릭합니다.

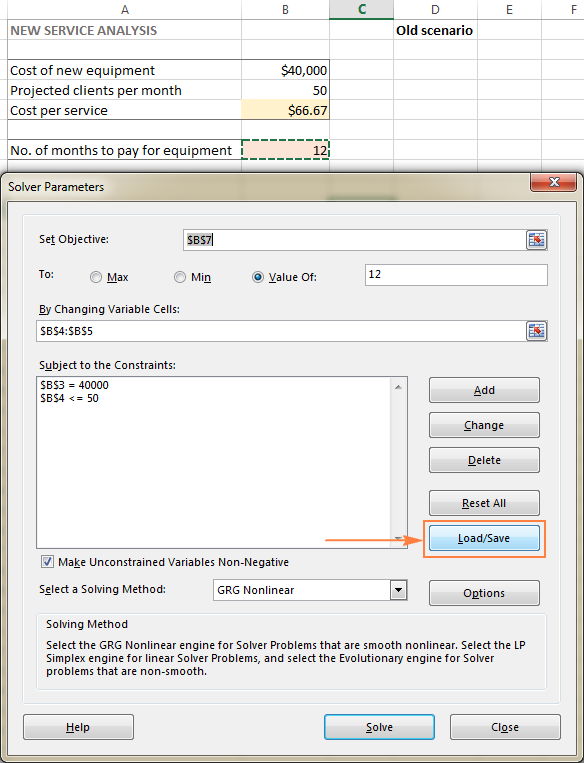
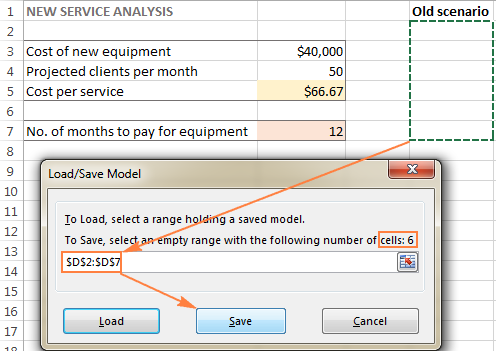
  • Excel Solver가 필요한 셀 수를 알려줍니다. 시나리오를 저장합니다. 비어 있는 셀을 많이 선택하고 저장 :

  • 을 클릭하면 Excel에서 현재 모델을 저장하며 다음과 같이 표시될 수 있습니다.

    • 동시에 Solver Parameters 창이 표시되어 제약 조건을 변경하고 다양한 "what if" 옵션을 시도할 수 있습니다.

    로드 중 저장된 모델

    저장된 시나리오를 복원하기로 결정한 경우 다음을 수행하십시오.

    1. 솔버 매개변수 창에서 로드/ 저장 버튼.
    2. 워크시트에서 저장된 모델이 있는 셀 범위를 선택하고 로드 :

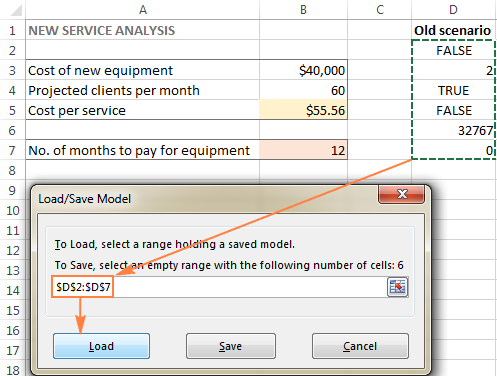    를 클릭합니다.

  • 모델 로드 대화 상자에서 바꾸기 버튼을 클릭합니다.

  • 이전에 저장된 모델의 매개변수. 다시 계산하려면 해결 버튼을 클릭하기만 하면 됩니다.

    • Excel 해 찾기 알고리즘

    Excel 해 찾기에 대한 문제를 정의할 때 다음을 선택할 수 있습니다. 해결 방법 선택 드롭다운 상자에서 다음 방법 중 하나:

    • GRG 비선형. Generalized Reduced Gradient Nonlinear 알고리즘은 매끄러운 비선형 문제, 즉 제약 조건 중 하나 이상이 결정 변수의 매끄러운 비선형 함수인 문제에 사용됩니다. 자세한 내용은 여기에서 확인할 수 있습니다.
    • LP Simplex . Simplex LP Solving 방법은 미국 수학 과학자 George Dantzig가 만든 Simplex 알고리즘을 기반으로 합니다. 소위 선형 프로그래밍 문제를 해결하는 데 사용됩니다. 요구 사항이 선형 관계로 특징지어지는 수학적 모델, 즉 최대화하거나 최소화해야 하는 선형 방정식으로 표현되는 단일 목표로 구성됩니다. 자세한 내용은 이 페이지를 확인하십시오.
    • 진화 . 일부 함수가 매끄럽지 않거나 심지어 불연속적이어서 함수가 증가하거나 감소하는 방향을 결정하기 어렵기 때문에 해결하기 가장 어려운 유형의 최적화 문제인 매끄럽지 않은 문제에 사용됩니다. 자세한 내용은 이 페이지를 참조하십시오.

    해 찾기가 솔루션을 찾는 방법을 변경하려면 해 찾기 매개 변수 대화 상자에서 옵션 버튼을 클릭하고 GRG Nonlinear , All Methods 및 Evolutionary 탭에서 일부 또는 모든 옵션을 구성합니다.

    Excel에서 Solver를 사용하는 방법입니다. 결정 문제에 대한 최상의 솔루션을 찾을 수 있습니다. 그리고 지금, 당신은 원할 수 있습니다이 자습서에서 설명하는 Excel 해 찾기 예제를 다운로드하고 더 나은 이해를 위해 리버스 엔지니어링하십시오. 읽어 주셔서 감사합니다. 다음 주 블로그에서 뵙기를 바랍니다.

    투자 수익 극대화, 광고 캠페인에 대한 최적의 예산 선택, 직원을 위한 최상의 작업 일정 만들기, 배송 비용 최소화 등.

    Excel에 Solver를 추가하는 방법

    해 찾기 추가 기능은 2003부터 모든 버전의 Microsoft Excel에 포함되어 있지만 기본적으로 활성화되어 있지는 않습니다.

    해 찾기를 Excel에 추가하려면 다음 단계를 수행하십시오.

    1. Excel 2010 - Excel 365에서 파일 > 옵션 을 클릭합니다.

      Excel 2007에서 Microsoft Office 버튼을 클릭하고 그런 다음 Excel 옵션 을 클릭합니다.

    2. Excel 옵션 대화 상자의 왼쪽 사이드바에서 추가 기능 을 클릭하고 Excel Add-ins 창 하단의 관리 상자에서 선택하고 이동 을 클릭합니다.
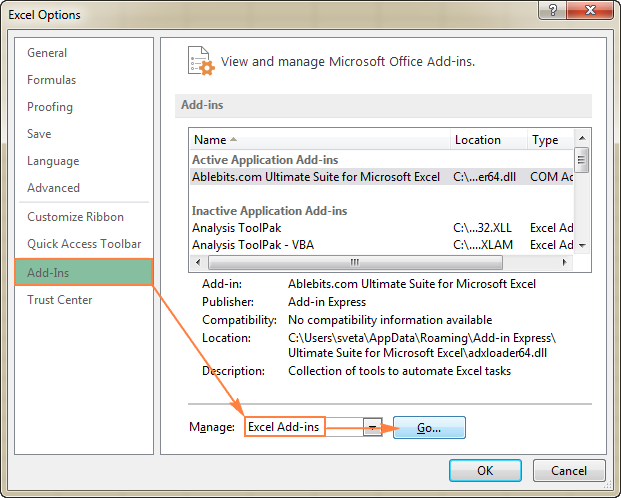
    3. Add-Ins 대화 상자에서 Solver Add-in 상자를 선택하고 확인 :

    을 클릭합니다.

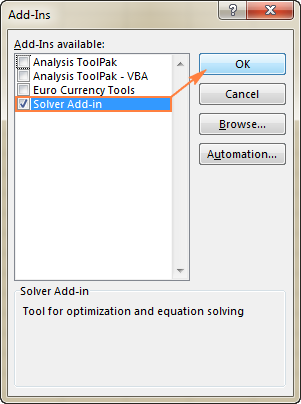
    Excel 2003 에서 Solver를 사용하려면 도구 메뉴로 이동하여 추가 기능 을 클릭하십시오. 추가 기능 사용 가능 목록에서 Solver 추가 기능 상자를 선택하고 확인 을 클릭합니다.

    메모. 컴퓨터에 Solver Add-in이 현재 설치되어 있지 않다는 메시지가 Excel에 표시되면 예 를 클릭하여 설치하십시오.

    Excel에서 Solver는 어디에 있습니까?

    최신 버전의 Excel에서는 Solver 버튼이 Data 탭의 Analysis 그룹:

    어디에Excel 2003의 해 찾기?

    해 찾기 추가 기능이 Excel 2003에 로드되면 해당 명령이 도구 메뉴에 추가됩니다.

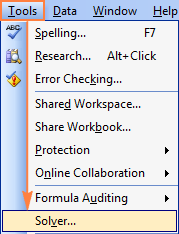
    이제 Excel에서 해 찾기를 찾을 수 있는 위치를 알았으므로 새 워크시트를 열고 시작하겠습니다!

    참고. 이 자습서에서 설명하는 예제는 Excel 2013의 해 찾기를 사용합니다. 다른 Excel 버전이 있는 경우 해 찾기 기능은 기본적으로 동일하지만 스크린샷이 버전과 정확히 일치하지 않을 수 있습니다.

    Excel에서 Solver 사용 방법

    Excel Solver 추가 기능을 실행하기 전에 해결하려는 모델을 워크시트에 공식화합니다. 이 예제에서는 다음과 같은 간단한 최적화 문제에 대한 솔루션을 찾아보겠습니다.

    문제 . 당신이 미용실의 주인이고 고객에게 새로운 서비스를 제공할 계획이라고 가정해 봅시다. 이를 위해서는 $40,000의 새 장비를 구입해야 하며 12개월 이내에 할부로 지불해야 합니다.

    목표 : 지불할 수 있는 서비스당 최소 비용을 계산합니다. 지정된 기간 내에 새 장비를 사용할 수 있습니다.

    이 작업을 위해 다음 모델을 만들었습니다.

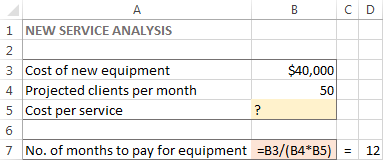
    이제 Excel Solver가 어떻게 이 문제에 대한 해결책을 찾으십시오.

    1. Excel Solver 실행

    Data 탭의 Analysis 그룹에서 Solver 버튼을 클릭합니다.

    2. 문제 정의

    Solver Parameters 창이 열릴 것입니다.3가지 기본 구성 요소를 설정합니다.

    • 목표 셀
    • 변수 셀
    • 제약 조건

    Excel Solver가 수행하는 작업 위의 매개변수? 변수 셀의 값을 변경하고 제약 조건의 제한에 따라 목표 셀의 수식에 대한 최적 값(최대, 최소 또는 지정)을 찾습니다. 셀.

    목표

    목표 셀(이전 Excel 버전의 목표 셀)은 수식을 포함하는 셀 입니다. 는 문제의 목표를 나타냅니다. 목적은 일부 목표 값을 최대화, 최소화 또는 달성하는 것일 수 있습니다.

    이 예에서 목표 셀은 B7이며 수식 =B3/(B4*B5) 을 사용하여 지불 조건을 계산하고 수식의 결과는 다음과 같아야 합니다. 12:

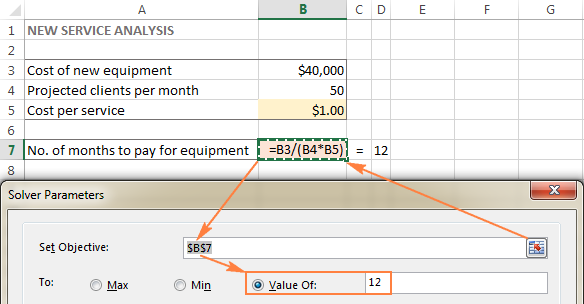
    가변 셀

    가변 셀( 변경 셀 또는 조정 가능 이전 버전의 셀)은 목표를 달성하기 위해 변경할 수 있는 변수 데이터를 포함하는 셀입니다. Excel Solver에서는 최대 200개의 변수 셀을 지정할 수 있습니다.

    이 예에는 값을 변경할 수 있는 두 개의 셀이 있습니다.

    • 월별 예상 클라이언트(B4) 50 이하; 및
    • Excel Solver가 계산할 서비스당 비용(B5).

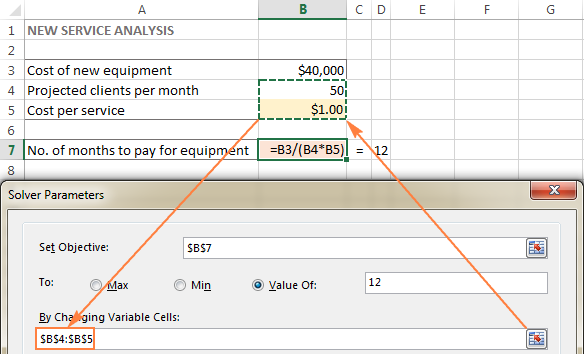
    팁. 모델의 변수 셀 또는 범위가 인접하지 않은 경우,첫 번째 셀 또는 범위를 선택한 다음 Ctrl 키를 누른 상태에서 다른 셀 및/또는 범위를 선택합니다. 또는 범위를 쉼표로 구분하여 수동으로 입력합니다.

    제약

    Excel 솔버 제약 은 문제에 대한 가능한 솔루션의 제한 또는 한계입니다. 달리 말하면 제약 조건은 충족되어야 하는 조건입니다.

    제약 조건을 추가하려면 다음을 수행하십시오.

    • 추가 " Subject to the Constraints " 상자 오른쪽에 있는 버튼을 클릭합니다.

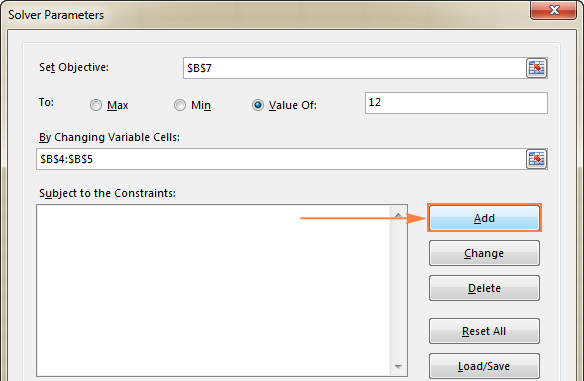
    • Constraint 창에서 제약 조건을 입력하십시오.
    • 목록에 제약 조건을 추가하려면 추가 버튼을 클릭하십시오.

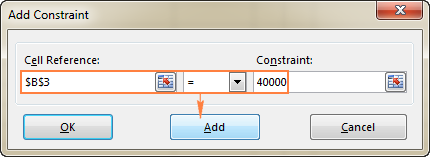
    • 계속 다른 제약 조건을 입력합니다.
    • 마지막 제약 조건을 입력한 후 확인 을 클릭하여 기본 Solver Parameters 창으로 돌아갑니다.

    Excel Solver를 사용하면 참조 셀과 제약 조건 사이에 다음과 같은 관계를 지정할 수 있습니다.

    • 작거나 같음 , 같음 및 보다 크거나 같습니다. 셀 참조 상자에서 셀을 선택하고 <= , =, 또는 > 기호 중 하나를 선택하여 이러한 관계를 설정합니다. ;= , Constraint 상자에 숫자, 셀 참조/셀 이름 또는 수식을 입력합니다(위 스크린샷 참조).
    • Integer . 참조 셀이 정수여야 하는 경우 int 를 선택하고,그리고 integer 라는 단어가 Constraint 상자에 나타납니다.
    • Different values . 참조 범위의 각 셀이 다른 값을 포함해야 하는 경우 dif 를 선택하면 Constraint 상자에 AllDifferent 라는 단어가 나타납니다.
    • 바이너리 . 참조 셀을 0 또는 1로 제한하려면 bin 을 선택하면 Constraint 상자에 binary 라는 단어가 나타납니다.

    참고. int , bin 및 dif 관계는 변수 셀의 제약 조건에만 사용할 수 있습니다.

    기존 제약 조건을 편집 또는 삭제 하려면 다음을 수행하십시오.

    • 솔버 매개변수 대화 상자에서 제약.
    • 선택한 제약을 수정하려면 변경 을 클릭하고 원하는 대로 변경합니다.
    • 제약을 삭제하려면 삭제 버튼을 클릭합니다. .

    이 예에서 제약 조건은 다음과 같습니다.

    • B3=40000 - 새 장비 비용은 $40,000입니다.
    • B4<=50 - 50세 미만의 월별 예상 환자 수.

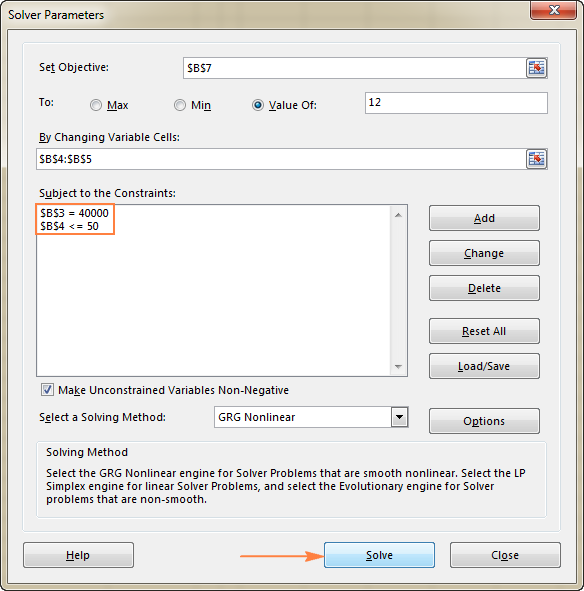
    3. 문제 해결

    모든 매개변수를 구성한 후 Solver Parameters 창 하단에 있는 Solve 버튼을 클릭하고(위 스크린샷 참조) Excel Solver 추가 기능은 문제에 대한 최적의 솔루션을 찾습니다.

    모델 복잡성, 컴퓨터 메모리 및 프로세서 속도에 따라 몇 시간이 걸릴 수 있습니다.몇 초, 몇 분 또는 몇 시간.

    해 찾기가 처리를 완료하면 해 찾기 결과 대화 상자 창이 표시되며 여기에서 해 찾기 솔루션 유지<를 선택합니다. 9> 확인 :

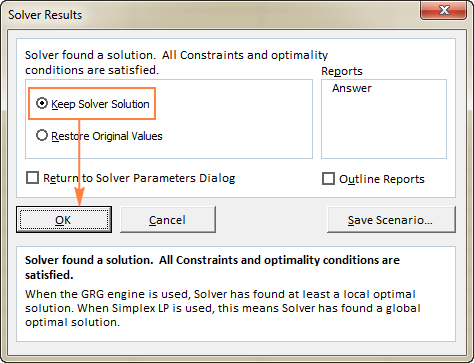
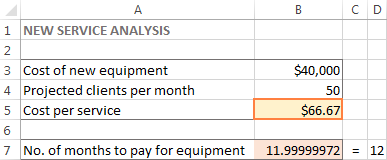
    Solver Result 창이 닫히고 솔루션이 나타납니다. 워크시트에 즉시 표시됩니다.

    이 예에서 셀 B5에는 $66.67이 표시됩니다. 이는 서비스당 최소 고객이 50명 이상인 경우 12개월 내에 새 장비에 대한 비용을 지불할 수 있는 서비스당 최소 비용입니다. 월:

    팁:

    • Excel 해 찾기가 특정 문제를 너무 오랫동안 처리한 경우 다음을 눌러 프로세스를 중단할 수 있습니다. Esc 키. Excel은 변수 셀에 대해 발견된 마지막 값으로 워크시트를 다시 계산합니다.
    • 해결된 문제에 대한 자세한 내용을 보려면 보고서 상자에서 보고서 유형을 클릭하십시오. 을 클릭한 다음 확인 을 클릭합니다. 새 워크시트에 보고서가 생성됩니다.

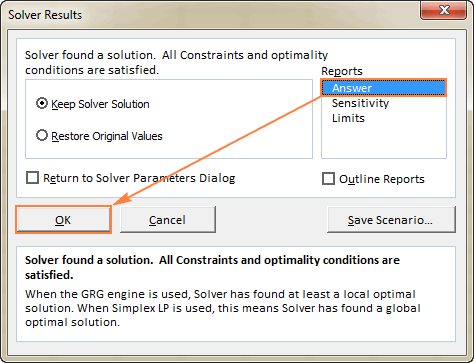
    이제 Excel에서 해 찾기를 사용하는 방법에 대한 기본 아이디어를 얻었으므로 몇 가지 방법을 자세히 살펴보겠습니다. 더 많은 이해를 돕는 더 많은 예제.

    Excel Solver 예제

    아래에서 Excel Solver 추가 기능을 사용하는 두 가지 예제를 더 찾을 수 있습니다. 먼저 잘 알려진 퍼즐에 대한 솔루션을 찾은 다음 실제 선형 프로그래밍 문제를 해결합니다.

    Excel Solver 예제 1(마법 사각형)

    I모든 행, 열 및 대각선의 합이 특정 숫자가 되도록 정사각형에 일련의 숫자를 넣어야 하는 "마법의 사각형" 퍼즐에 익숙할 것입니다.

    예를 들어, 각 행, 열 및 대각선의 합이 15인 1에서 9까지의 숫자를 포함하는 3x3 정사각형의 솔루션은 무엇입니까?

    시행착오를 통해 이 퍼즐을 푸는 것은 별 문제가 아니지만 Solver가 찾을 것이라고 장담합니다. 솔루션이 더 빨라집니다. 우리가 할 일은 문제를 적절하게 정의하는 것입니다.

    먼저 3행 3열로 구성된 표에 1부터 9까지의 숫자를 입력합니다. Excel 해 찾기에는 실제로 이러한 숫자가 필요하지 않지만 문제를 시각화하는 데 도움이 됩니다. Excel 해 찾기 추가 기능에 실제로 필요한 것은 각 행, 열 및 2개의 대각선을 합산하는 SUM 수식입니다.

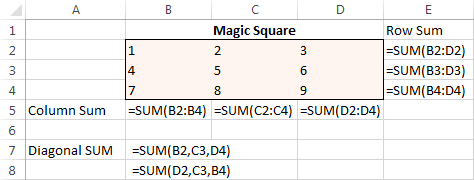
    모든 수식이 준비되면 해 찾기를 실행하고 설정합니다. 다음 매개변수:

    • 설정 목표 . 이 예에서는 목표를 설정할 필요가 없으므로 이 상자를 비워 둡니다.
    • 변수 셀 . 셀 B2에서 D4까지 숫자를 채우려면 B2:D4.
    • Constraints 범위를 선택합니다. 다음 조건이 충족되어야 합니다.
      • $B$2:$D$4 = AllDifferent - 모든 변수 셀은 서로 다른 값을 포함해야 합니다.
      • $B$2:$D$4 = 정수 - 모두 의 변수 셀은 정수여야 합니다.
      • $B$5:$D$5 = 15 - 각 셀의 값 합계열은 15와 같아야 합니다.
      • $E$2:$E$4 = 15 - 각 행의 값 합계는 15와 같아야 합니다.
      • $B$7:$B$8 = 15 - 합계는 두 대각선의 값은 15여야 합니다.

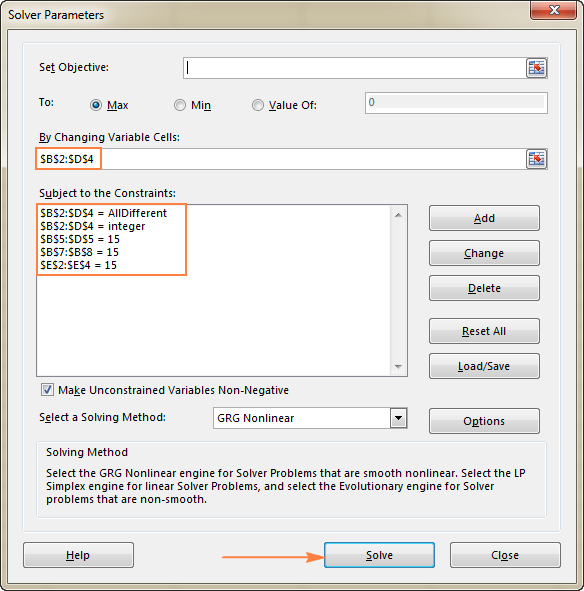
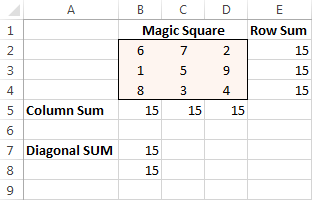
    마지막으로 해결 버튼을 클릭하면 해결 방법이 있습니다!

    Excel Solver 예제 2(선형 프로그래밍 문제)

    이는 선형 목표를 가진 간단한 운송 최적화 문제의 예제입니다. 이러한 종류의 더 복잡한 최적화 모델은 매년 수천 달러를 절약하기 위해 많은 회사에서 사용됩니다.

    문제 : 2개의 서로 다른 창고에서 4개의 서로 다른 창고로 상품을 배송하는 비용을 최소화하려고 합니다. 고객. 각 창고에는 공급이 제한되어 있고 각 고객에게는 특정 수요가 있습니다.

    목표 : 각 창고에서 사용할 수 있는 수량을 초과하지 않고 총 배송 비용을 최소화하고 각 고객의 수요를 충족합니다. .

    소스 데이터

    운송 최적화 문제는 다음과 같습니다.

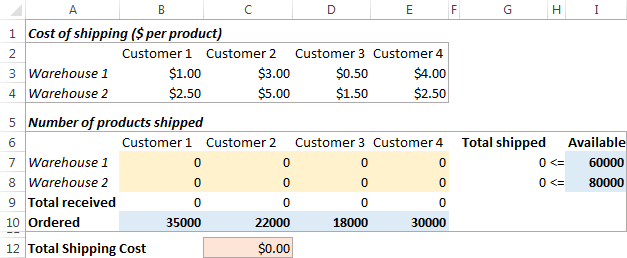
    모델 공식화

    To Excel Solver에 대한 선형 프로그래밍 문제를 정의하고 3가지 주요 질문에 답해 보겠습니다.

    1. 어떤 결정을 내려야 합니까? 각 창고에서 각 고객에게 배송할 최적의 상품 수량을 계산하려고 합니다. 이들은 변수 셀(B7:E8)입니다.
    2. 제약 사항은 무엇입니까? 각 창고(I7:I8)에서 사용 가능한 공급량을 초과할 수 없으며,
    다음 게시물 Google 스프레드시트의 셀을 여러 열로 분할하고 나중에 행으로 변환

    Michael Brown은 소프트웨어 도구를 사용하여 복잡한 프로세스를 단순화하려는 열정을 가진 열성적인 기술 애호가입니다. 기술 산업에서 10년 이상의 경험을 쌓은 그는 Microsoft Excel 및 Outlook은 물론 Google 스프레드시트 및 문서 도구에 대한 기술을 연마했습니다. Michael의 블로그는 자신의 지식과 전문 지식을 다른 사람과 공유하는 데 전념하며 따라하기 쉬운 팁과 생산성 및 효율성 향상을 위한 자습서를 제공합니다. 노련한 전문가이든 초보자이든 Michael의 블로그는 이러한 필수 소프트웨어 도구를 최대한 활용하기 위한 귀중한 통찰력과 실용적인 조언을 제공합니다.