Innehållsförteckning
I handledningen förklaras hur du lägger till och var du hittar Solver i olika Excel-versioner, från 2016 till 2003. Steg-för-steg-exempel visar hur du använder Excel Solver för att hitta optimala lösningar för linjär programmering och andra typer av problem.
Alla vet att Microsoft Excel innehåller många användbara funktioner och kraftfulla verktyg som kan spara dig timmar av beräkningar. Men visste du att det också finns ett verktyg som kan hjälpa dig att hitta optimala lösningar på beslutsproblem?
I den här handledningen kommer vi att täcka alla viktiga aspekter av Excel Solver-tillägget och ge en steg-för-steg-guide om hur du använder det mest effektivt.
Vad är Excel Solver?
Excel Solver tillhör en särskild uppsättning kommandon som ofta kallas What-if Analysis Tools och är främst avsedd för simulering och optimering av olika affärs- och tekniska modeller.
Tilläggsprogrammet Excel Solver är särskilt användbart för att lösa linjära programmeringsproblem, även kallade linjära optimeringsproblem, och kallas därför ibland för en Lösare för linjär programmering Dessutom kan den hantera jämna, icke-linjära och icke-flytande problem. Se Excel Solver-algoritmer för mer information.
Även om Solver inte kan lösa alla tänkbara problem är det mycket användbart när det gäller alla typer av optimeringsproblem där du måste fatta det bästa beslutet. Det kan till exempel hjälpa dig att maximera avkastningen på dina investeringar, välja den optimala budgeten för din reklamkampanj, göra det bästa arbetsschemat för dina anställda, minimera leveranskostnaderna och så vidare.
Hur du lägger till Solver i Excel
Tillägget Solver ingår i alla versioner av Microsoft Excel från och med 2003, men det är inte aktiverat som standard.
För att lägga till Solver i Excel, utför följande steg:
- I Excel 2010 - Excel 365 klickar du på Fil > Alternativ .
I Excel 2007 klickar du på Microsoft Office och klickar sedan på Excel-alternativ .
- I Excel-alternativ dialogrutan, klicka på Tilläggsfunktioner i den vänstra sidofältet, se till att Excel-tillägg väljs i Hantera längst ner i fönstret och klicka på Gå till .
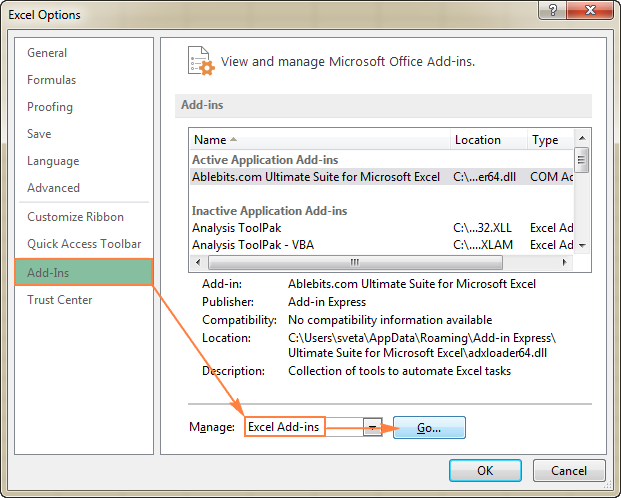
- I Tilläggsfunktioner dialogrutan, kryssa för Tillägg till Solver och klicka på OK :
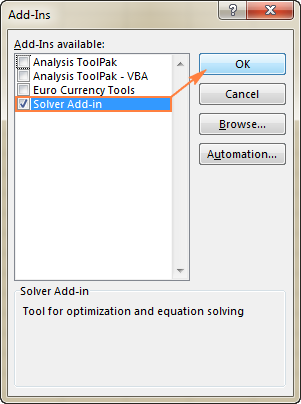
För att få Solver på Excel 2003 , gå till Verktyg menyn och klicka på Tilläggsfunktioner . I den Tilläggsfunktioner tillgänglig listan, kontrollera Tillägg till Solver och klickar på OK .
Obs. Om Excel visar ett meddelande om att tillägget Solver inte är installerat på din dator klickar du på Ja för att installera den.
Var finns Solver i Excel?
I de moderna versionerna av Excel är Lösare knappen visas på Uppgifter på fliken Analys grupp:

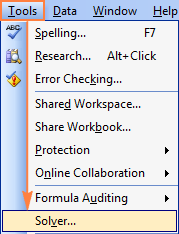
Var finns Solver i Excel 2003?
När tilläggsmodulen Solver har laddats in i Excel 2003 läggs kommandot till i Verktyg meny:
Nu när du vet var du hittar Solver i Excel öppnar du ett nytt kalkylblad och sätter igång!
Observera: Exemplen som diskuteras i den här handledningen använder Solver i Excel 2013. Om du har en annan Excel-version kanske skärmdumparna inte stämmer exakt överens med din version, även om Solver-funktionen i princip är densamma.
Hur du använder Solver i Excel
Innan du kör tilläggsmodulen Excel Solver ska du formulera den modell du vill lösa i ett arbetsblad. I det här exemplet ska vi hitta en lösning på följande enkla optimeringsproblem.
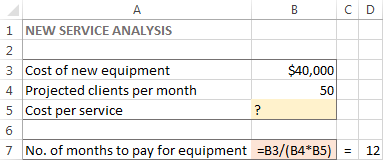
Problem Om du är ägare till en skönhetssalong och planerar att erbjuda dina kunder en ny tjänst, behöver du köpa en ny utrustning som kostar 40 000 dollar och som ska betalas på avbetalning inom 12 månader.
Mål : Beräkna den lägsta kostnaden per tjänst som gör att du kan betala för den nya utrustningen inom den angivna tidsramen.
För den här uppgiften har jag skapat följande modell:
Nu ska vi se hur Excel Solver kan hitta en lösning på det här problemet.
1. Kör Excel Solver
På den Uppgifter på fliken Analys grupp, klickar du på Lösare knapp.
2. Definiera problemet
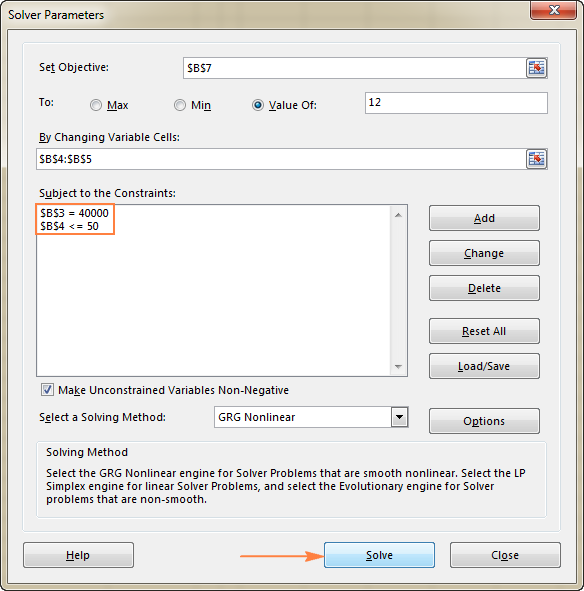
Parametrar för lösaren öppnas ett fönster där du måste ställa in de tre huvudkomponenterna:
- Målcell
- Variabla celler
- Begränsningar
Exakt vad gör Excel Solver med ovanstående parametrar? Den hittar det optimala värdet (maximalt, minimalt eller specificerat) för formeln i Mål cellen genom att ändra värdena i Variabel celler, och med förbehåll för begränsningar i Begränsningar celler.
Mål
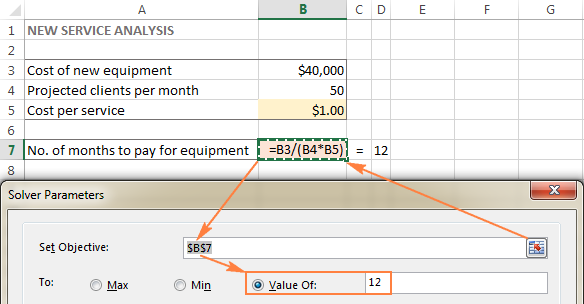
Mål cell ( Mål cell i tidigare Excel-versioner) är cellen som innehåller en formel som representerar problemets mål, som kan vara att maximera, minimera eller uppnå ett visst målvärde.
I det här exemplet är målcellen B7, som beräknar betalningstiden med hjälp av formeln =B3/(B4*B5) och resultatet av formeln ska vara lika med 12:
Variabla celler
Variabel celler ( Ändring av celler eller Justerbar celler i tidigare versioner) är celler som innehåller variabla data som kan ändras för att uppnå målet. Excel Solver gör det möjligt att ange upp till 200 variabla celler.
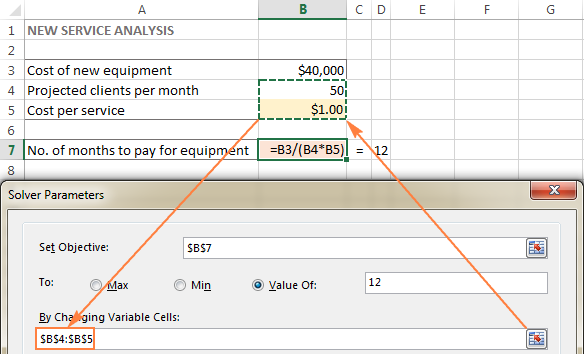
I det här exemplet har vi ett par celler vars värden kan ändras:
- Förväntade kunder per månad (B4) som bör vara högst 50, och
- Kostnad per tjänst (B5) som vi vill att Excel Solver ska beräkna.
Tips: Om de variabla cellerna eller områdena i modellen är Icke angränsande , markera den första cellen eller det första intervallet och håll sedan ned Ctrl-tangenten medan du markerar andra celler och/eller intervall. Du kan också skriva in intervallerna manuellt, separerade med kommatecken.
Begränsningar
Excel Solver Begränsningar är begränsningar eller gränser för de möjliga lösningarna på problemet. Med andra ord är begränsningar de villkor som måste uppfyllas.
Gör följande för att lägga till en eller flera begränsningar:
- Klicka på Lägg till till höger om " Med förbehåll för de begränsningar som gäller ".
- I Begränsning och ange en begränsning.
- Klicka på Lägg till för att lägga till begränsningen i listan.
- Fortsätt att ange andra begränsningar.
- När du har angett den sista begränsningen klickar du på OK för att återgå till huvudsidan Lösare Parametrar fönster.
Excel Solver gör det möjligt att ange följande relationer mellan den refererade cellen och begränsningen.
- Mindre än eller lika med , är lika med , och är större än eller lika med Du ställer in dessa relationer genom att välja en cell i Cellreferens och välj ett av följande tecken: <= , =, eller . >= och sedan skriva ett nummer, en cellreferens/cellnamn eller en formel i fältet Begränsning (se skärmbilden ovan).
- Heltal Om den refererade cellen måste vara ett heltal väljer du int , och ordet heltal kommer att visas i Begränsning box.
- Olika värden Om varje cell i det refererade intervallet måste innehålla ett annat värde väljer du dif , och ordet AllDifferent kommer att visas i Begränsning box.
- Binary Om du vill begränsa en refererad cell till 0 eller 1 väljer du bin , och ordet binär kommer att visas i Begränsning box.
Observera. int , bin , och dif kan endast användas för begränsningar på variabla celler.
Till redigera eller . ta bort en befintlig begränsning göra följande:
- I Parametrar för lösaren dialogrutan, klicka på begränsningen.
- Om du vill ändra den valda begränsningen klickar du på Ändra och gör de ändringar du vill.
- Om du vill ta bort begränsningen klickar du på Ta bort knapp.
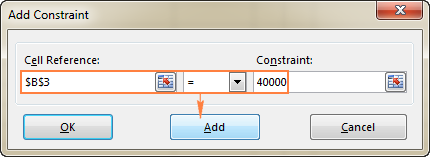
I det här exemplet är begränsningarna:
- B3=40000 - kostnaden för den nya utrustningen är 40 000 dollar.
- B4<=50 - antalet beräknade patienter per månad under 50.
3. Lös problemet
När du har konfigurerat alla parametrar klickar du på knappen Lös knappen längst ner i Parametrar för lösaren (se skärmbilden ovan) och låt Excel Solver-tillägget hitta den optimala lösningen för ditt problem.
Beroende på modellens komplexitet, datorminne och processorhastighet kan det ta några sekunder, några minuter eller till och med några timmar.
När Solver har avslutat bearbetningen kommer den att visa Resultat av lösningen dialogfönstret, där du väljer Behåll lösaren Lösningen och klicka på OK :
Lösare Resultat fönstret stängs och lösningen visas direkt på arbetsbladet.
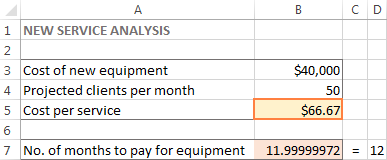
I det här exemplet visas 66,67 dollar i cell B5, vilket är den minimikostnad per tjänst som gör att du kan betala för den nya utrustningen på 12 månader, förutsatt att det finns minst 50 kunder per månad:
Tips:
- Om Excel Solver har behandlat ett visst problem för länge kan du avbryta processen genom att trycka på Esc-tangenten. Excel räknar om kalkylbladet med de senaste värdena som hittats för problemet. Variabel celler.
- Om du vill få mer information om det lösta problemet klickar du på en rapporttyp i Rapporter och klicka sedan på OK Rapporten skapas på ett nytt arbetsblad:
Nu när du har fått den grundläggande idén om hur du använder Solver i Excel, ska vi titta närmare på några fler exempel som kan hjälpa dig att få en bättre förståelse.
Exempel på Excel Solver
Nedan hittar du ytterligare två exempel på hur du kan använda Excel Solver-tillägget. Först hittar vi en lösning på ett välkänt pussel och sedan löser vi ett verkligt linjärt programmeringsproblem.
Excel Solver exempel 1 (magisk kvadrat)
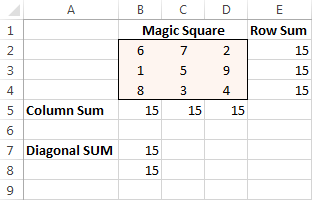
Jag tror att alla är bekanta med pussel med "magiska kvadrater" där man måste placera en uppsättning siffror i en kvadrat så att alla rader, kolumner och diagonaler summerar till ett visst antal.
Känner du till exempel till en lösning för 3x3-kvadraten med siffror från 1 till 9 där varje rad, kolumn och diagonal summerar till 15?
Det är förmodligen ingen stor sak att lösa det här pusslet genom försök och misstag, men jag slår vad om att Solver kommer att hitta lösningen snabbare. Vår del av arbetet är att definiera problemet på rätt sätt.
Till att börja med skriver du in siffrorna från 1 till 9 i en tabell som består av 3 rader och 3 kolumner. Excel Solver behöver egentligen inte dessa siffror, men de hjälper oss att visualisera problemet. Vad Excel Solver-tillägget verkligen behöver är SUMM-formlerna som summerar varje rad, kolumn och 2 diagonaler:
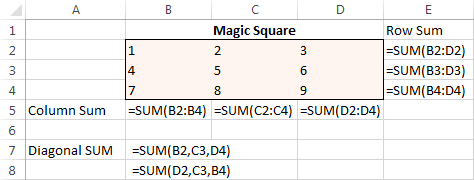
När alla formler är på plats kör du Solver och ställer in följande parametrar:
- Ställ in Mål I det här exemplet behöver vi inte ange något mål, så låt denna ruta vara tom.
- Variabla celler . Vi vill fylla på siffror i cellerna B2 till D4, så välj intervallet B2:D4.
- Begränsningar Följande villkor ska vara uppfyllda:
- $B$2:$D$4 = AllDifferent - alla variabla celler ska innehålla olika värden.
- $B$2:$D$4 = heltal - alla variabla celler ska vara heltal.
- $B$5:$D$5 = 15 - summan av värdena i varje kolumn ska vara lika med 15.
- $E$2:$E$4 = 15 - summan av värdena i varje rad ska vara lika med 15.
- $B$7:$B$8 = 15 - summan av de båda diagonalerna ska vara lika med 15.
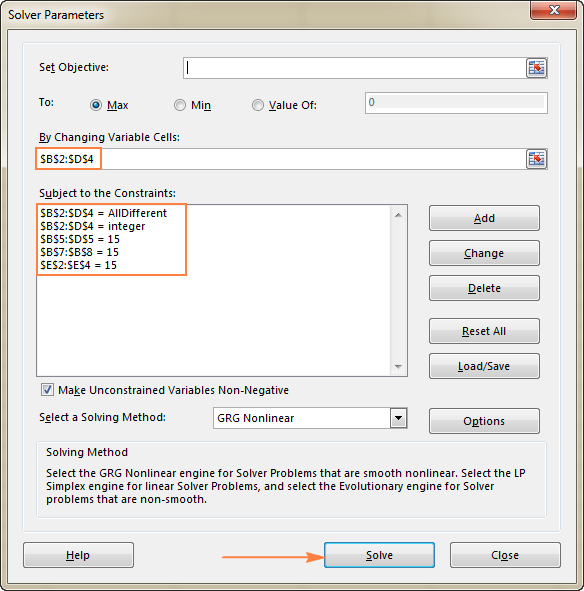
Slutligen klickar du på Lös knappen, och lösningen finns där!
Excel Solver exempel 2 (problem med linjär programmering)
Detta är ett exempel på ett enkelt transportoptimeringsproblem med ett linjärt mål. Mer komplexa optimeringsmodeller av detta slag används av många företag för att spara tusentals dollar varje år.
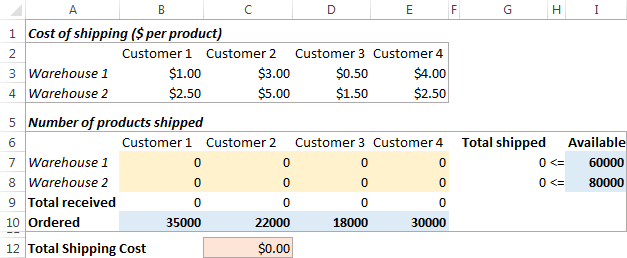
Problem : Du vill minimera kostnaden för att skicka varor från två olika lager till fyra olika kunder. Varje lager har ett begränsat utbud och varje kund har en viss efterfrågan.
Mål : Minimera den totala fraktkostnaden, utan att överskrida den kvantitet som finns tillgänglig på varje lager och uppfylla varje kunds efterfrågan.
Källdata
Så här ser vårt transportoptimeringsproblem ut:
Formulering av modellen
För att definiera vårt linjära programmeringsproblem för Excel Solver ska vi besvara de tre huvudfrågorna:
- Vilka beslut ska fattas? Vi vill beräkna den optimala mängden varor som ska levereras till varje kund från varje lager. Dessa är följande Variabel celler (B7:E8).
- Vad är begränsningarna? De tillgängliga förråden på varje lager (I7:I8) får inte överskridas och den kvantitet som beställts av varje kund (B10:E10) ska levereras. Dessa är Begränsad celler .
- Vad är målet? En så låg totalkostnad som möjligt för transporten. Och detta är vårt mål. Mål cell (C12).
Nästa steg är att beräkna den totala kvantiteten som skickats från varje lager (G7:G8) och den totala mängden varor som varje kund tagit emot (B9:E9). Du kan göra detta med enkla summformler som visas i skärmdumpen nedan. Infoga också formeln SUMPRODUCT i C12 för att beräkna den totala fraktkostnaden:
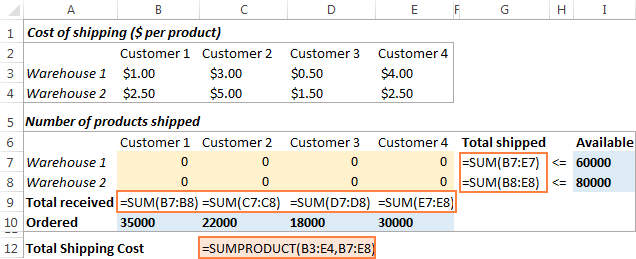
För att göra vår modell för transportoptimering lättare att förstå skapar vi följande namngivna områden:
| Namn på intervallet | Celler | Parameter för lösaren |
| Produkter_skickade | B7:E8 | Variabla celler |
| Tillgänglig | I7:I8 | Begränsning |
| Total_shipped | G7:G8 | Begränsning |
| Beställd | B10:E10 | Begränsning |
| Total_received | B9:E9 | Begränsning |
| Frakt_kostnad | C12 | Mål |
Det sista du behöver göra är att konfigurera parametrarna för Excel Solver:
- Mål: Shipping_cost fastställs till Min
- Variabla celler: Products_shipped
- Restriktioner: Total_received = Beställd och Total_shipped <= Tillgänglig
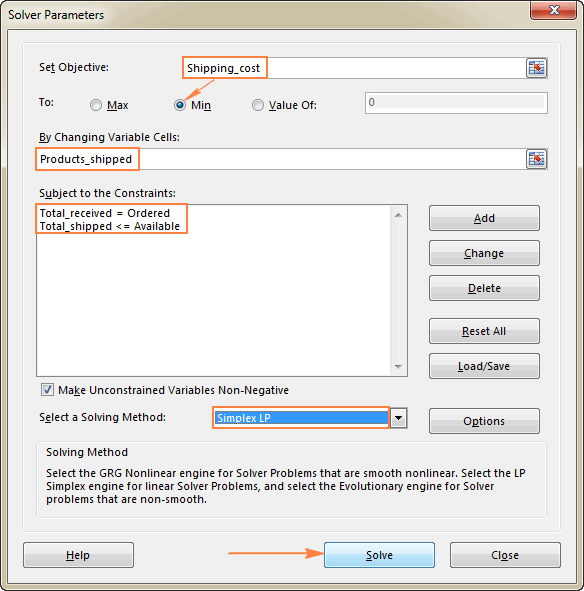
Var uppmärksam på att vi har valt den Simplex LP i det här exemplet eftersom vi har att göra med ett problem med linjär programmering. Om du inte är säker på vilken typ av problem det rör sig om i ditt fall, kan du låta standardinställningen GRG Icke-linjärt För mer information, se Excel Solver-algoritmer.
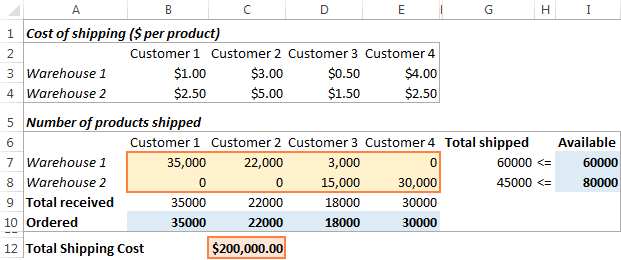
Lösning
Klicka på Lös knappen längst ner i Parametrar för lösaren I det här exemplet beräknade tilläggsmodulen Excel Solver den optimala mängden varor som ska levereras till varje kund från varje lager med minsta möjliga totala fraktkostnad:
Hur du sparar och laddar Excel Solver-scenarier
När du löser en viss modell kanske du vill spara din Variabel cellvärden som ett scenario som du kan visa eller återanvända senare.
När du beräknar den lägsta servicekostnaden i det första exemplet i den här handledningen kanske du vill prova olika antal kunder per månad och se hur det påverkar servicekostnaden. Du kanske vill spara det mest sannolika scenariot som du redan har beräknat och återställa det när som helst.
Spara ett Excel Solver-scenario går ut på att välja ett cellintervall att spara data i. Laddar en Solver-modell är bara en fråga om att ge Excel det cellintervall där modellen är sparad. De detaljerade stegen följer nedan.
Spara modellen
För att spara Excel Solver-scenariot utför du följande steg:
- Öppna arbetsbladet med den beräknade modellen och kör Excel Solver.
- I Parametrar för lösaren fönstret, klickar du på Ladda/Spara knapp.
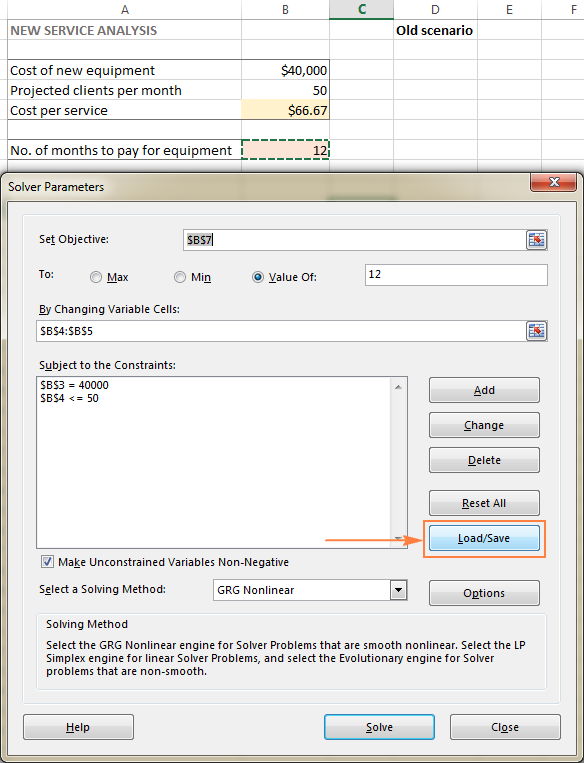
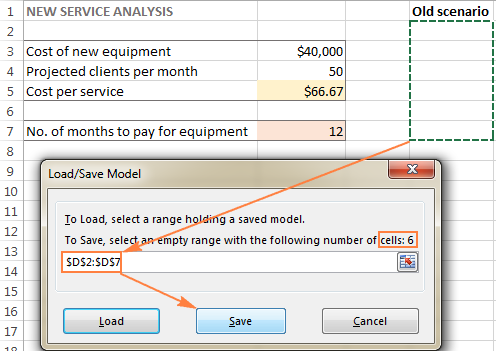
Samtidigt har Parametrar för lösaren öppnas ett fönster där du kan ändra dina begränsningar och pröva olika "vad händer om"-alternativ.
Laddning av den sparade modellen
När du bestämmer dig för att återställa det sparade scenariot gör du följande:
- I Parametrar för lösaren fönstret, klickar du på Ladda/Spara knapp.
- På arbetsbladet markerar du det cellområde som innehåller den sparade modellen och klickar på Ladda :
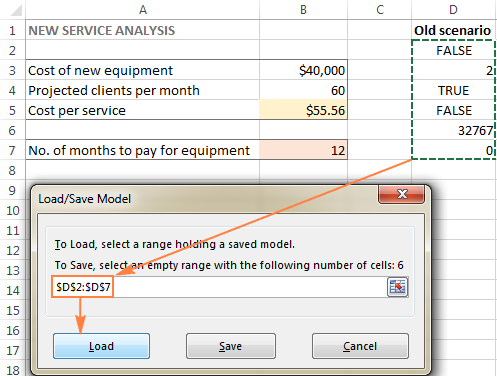
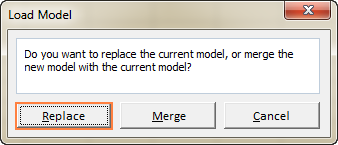
Excel Solver-algoritmer
När du definierar ett problem för Excel-lösaren kan du välja en av följande metoder i Välj en lösningsmetod rullgardinsrutan:
- GRG Icke linjärt. Generaliserad reducerad gradient Icke-linjär Algoritmen används för problem som är mjuka icke-linjära, dvs. där minst ett av begränsningarna är en mjuk icke-linjär funktion av beslutsvariablerna.
- LP Simplex Simplex LP-lösningsmetoden bygger på Simplex-algoritmen som skapades av den amerikanske matematikforskaren George Dantzig och används för att lösa så kallade Linjär programmering problem - matematiska modeller vars krav kännetecknas av linjära förhållanden, dvs. består av ett enda mål som representeras av en linjär ekvation som måste maximeras eller minimeras. För mer information, se den här sidan.
- Evolutionär Den används för icke-goda problem, som är den svåraste typen av optimeringsproblem att lösa eftersom vissa funktioner är icke-goda eller till och med diskontinuerliga och det därför är svårt att avgöra i vilken riktning en funktion ökar eller minskar. För mer information, se den här sidan.
Om du vill ändra hur Solver hittar en lösning klickar du på Alternativ knappen i den Parametrar för lösaren och konfigurera något eller några av alternativen i dialogrutan GRG Icke-linjärt , Alla metoder , och Evolutionär flikar.
Så här kan du använda Solver i Excel för att hitta de bästa lösningarna för dina beslutsproblem. Och nu kanske du vill ladda ner Excel Solver-exemplen som diskuteras i den här handledningen och göra dem om för att få en bättre förståelse. Jag tackar dig för att du läste och hoppas att vi ses på vår blogg nästa vecka.

