INHOUDSOPGAWE
Die tutoriaal verduidelik hoe om by te voeg en waar om Solver in verskillende Excel-weergawes te vind, van 2016 tot 2003. Stap-vir-stap voorbeelde wys hoe om Excel Solver te gebruik om optimale oplossings vir lineêre programmering en ander soorte probleme.
Almal weet dat Microsoft Excel baie nuttige funksies en kragtige hulpmiddels bevat wat jou ure se berekeninge kan bespaar. Maar het jy geweet dat dit ook 'n hulpmiddel het wat jou kan help om optimale oplossings vir besluiteprobleme te vind?
In hierdie tutoriaal gaan ons alle noodsaaklike aspekte van die Excel Solver-byvoeging dek en 'n stap verskaf -vir-stap gids oor hoe om dit die doeltreffendste te gebruik.
Wat is Excel Solver?
Excel Solver behoort aan 'n spesiale stel van opdragte wat dikwels na verwys word as Wat-as-analise-nutsgoed. Dit is hoofsaaklik bedoel vir simulasie en optimalisering van verskeie besigheids- en ingenieursmodelle.
Die Excel Solver-byvoeging is veral nuttig vir die oplossing van lineêre programmeringsprobleme, oftewel lineêre optimaliseringsprobleme, en word daarom soms 'n genoem. lineêre programmeringsoplosser . Daarbenewens kan dit gladde nie-lineêre en nie-gladde probleme hanteer. Sien asseblief Excel Oplosser-algoritmes vir meer besonderhede.
Terwyl Oplosser nie elke moontlike probleem kan kraak nie, is dit regtig nuttig wanneer u met allerhande optimeringsprobleme te doen het waar u die beste besluit moet neem. Dit kan byvoorbeeldhoeveelheid wat deur elke klant bestel is (B10:E10) moet afgelewer word. Dit is Beperkte selle .
Die volgende ding wat jy moet doen is om die totale hoeveelheid wat vanaf elke pakhuis verskeep is, te bereken (G7:G8), en die totale goedere ontvang deur elke kliënt (B9:E9). Jy kan dit doen met eenvoudige Som-formules wat in die onderstaande skermkiekie gedemonstreer word. Voeg ook die SUMPRODUCT-formule in C12 in om die totale koste van versending te bereken:
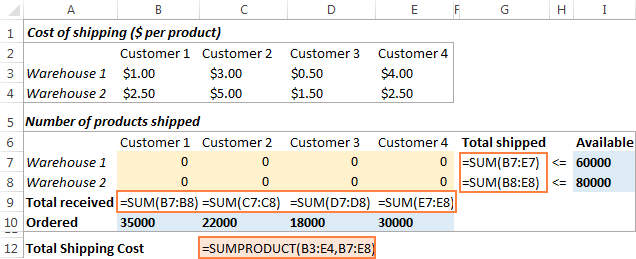
Om ons vervoeroptimeringsmodel makliker te verstaan, skep die volgende genoemde reekse:
| Reeksnaam | Selle | Oplosparameter |
| Produkte_verskeep | B7: E8 | Veranderlike selle |
| Beskikbaar | I7:I8 | Beperking |
| Totaal_verskeep | G7:G8 | Beperking |
| Bestel | B10:E10 | Beperking |
| Totaal_ontvang | B9:E9 | Beperking |
| Verstuurkoste | C12 | Doelwit |
Die laaste ding wat vir jou oorbly om te doen is om die Excel Oplosser-parameters op te stel:
- Doelwit: Versendingkoste gestel op Min.
- Veranderlike selle: Produkte_verskeep
- Beperkings: Totaal_ontvang = Bestel en Totaal_verskeep <= Beskikbaar
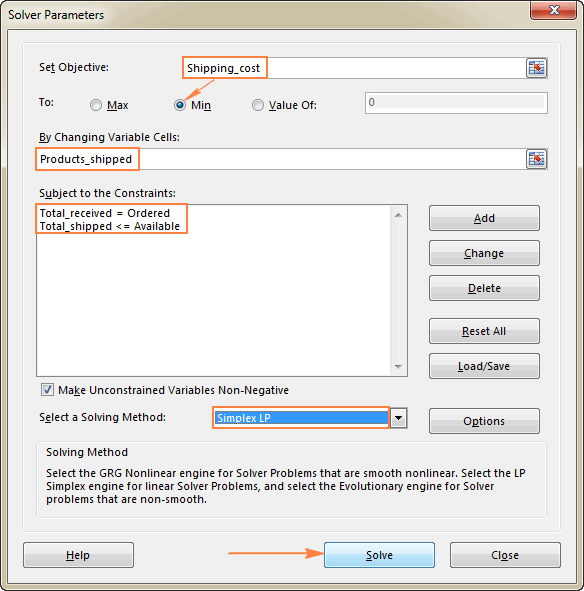
Betaal asseblief aandag wat ons gekies hetdie Simplex LP -oplossingsmetode in hierdie voorbeeld omdat ons met die lineêre programmeringsprobleem te doen het. As jy nie seker is watter soort probleem joune is nie, kan jy die verstek GRG Nie-lineêre oplosmetode verlaat. Vir meer inligting, sien asseblief Excel Solver-algoritmes.
Oplossing
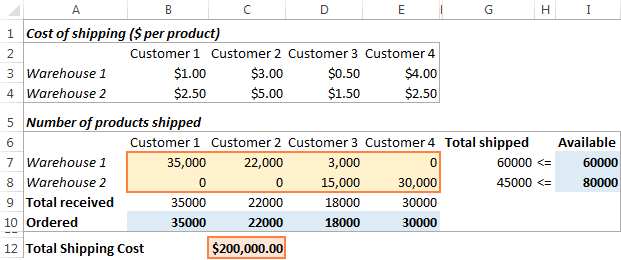
Klik die Los op -knoppie onderaan die Oplosserparameters -venster, en jy sal jou antwoord kry. In hierdie voorbeeld het die Excel Solver-byvoeging die optimale hoeveelheid goedere bereken om aan elke klant van elke pakhuis te lewer met die minimale totale koste van versending:
Hoe om te spaar en laai Excel Solver-scenario's
Wanneer jy 'n sekere model oplos, wil jy dalk jou Veranderlike -selwaardes stoor as 'n scenario wat jy later kan bekyk of hergebruik.
Byvoorbeeld, wanneer jy die minimale dienskoste in die heel eerste voorbeeld wat in hierdie tutoriaal bespreek word, bereken, wil jy dalk verskillende getalle geprojekteerde kliënte per maand probeer en sien hoe dit die dienskoste beïnvloed. Dan wil jy dalk die mees waarskynlike scenario wat jy reeds bereken het stoor en dit enige oomblik herstel.
Stoor 'n Excel Solver scenario kom daarop neer om 'n reeks selle te kies om stoor die data in. Laai 'n Oplosser-model is net 'n kwessie daarvan om Excel te voorsien van die reeks selle waar jou model gestoor word. Die gedetailleerde stappe volg hieronder.
Stoor diemodel
Om die Excel Solver-scenario te stoor, voer die volgende stappe uit:
- Maak die werkblad met die berekende model oop en laat loop die Excel Solver.
- In die Oplosser Parameters venster, klik die Laai/Stoor knoppie.
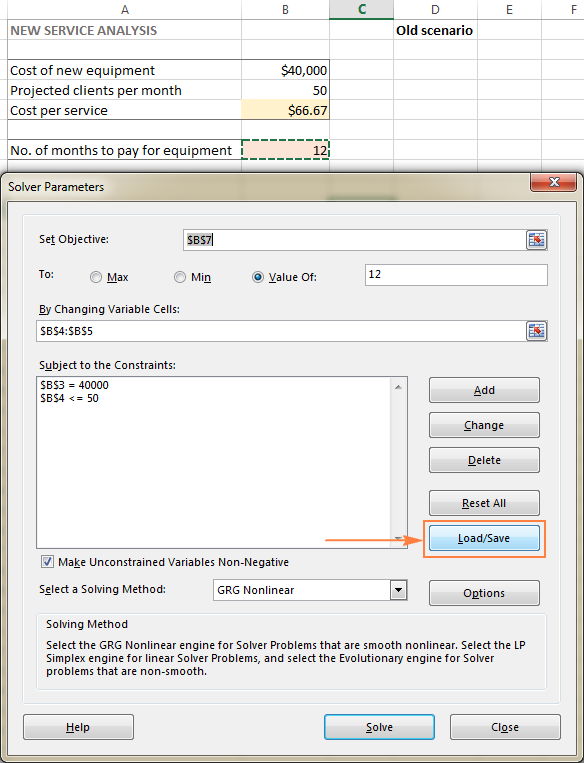
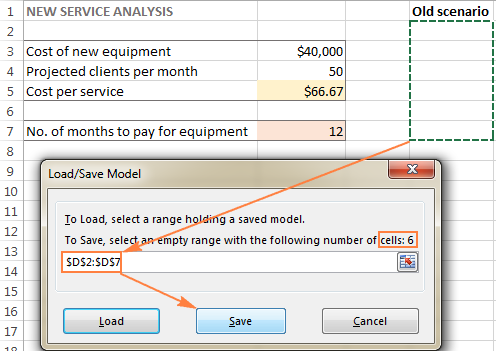
Terselfdertyd sal die Oplosserparameters -venster verskyn waar jy jou beperkings kan verander en verskillende "wat as"-opsies kan probeer.
Laai die gestoorde model
Wanneer jy besluit om die gestoorde scenario te herstel, doen die volgende:
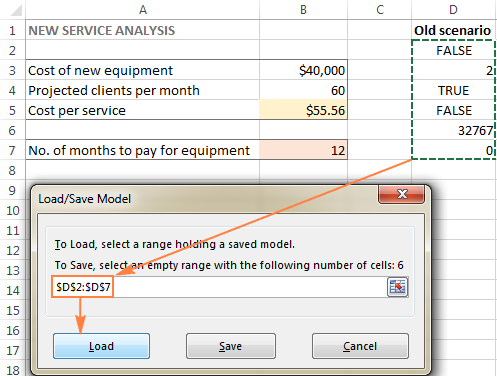
- In die Oplosserparameters -venster, klik die Laai/ Stoor -knoppie.
- Op die werkblad, kies die reeks selle wat die gestoorde model bevat en klik Laai :
Excel Solver-algoritmes
Wanneer jy 'n probleem vir die Excel-oplosser definieer, kan jy kies een van die volgende metodes in die Kies 'n Oplossingsmetode -aftreklys:
- GRG Nie-lineêr. Algemeen Verminderde Gradiënt Nie-lineêre -algoritme word gebruik vir probleme wat glad nie-lineêr is, dit wil sê waarin ten minste een van die beperkings 'n gladde nie-lineêre funksie van die besluitveranderlikes is. Meer besonderhede kan hier gevind word.
- LP Simplex . Die Simplex LP Solving-metode is gebaseer op die Simplex-algoritme wat deur 'n Amerikaanse wiskundige wetenskaplike George Dantzig geskep is. Dit word gebruik vir die oplossing van sogenaamde Lineêre Programmering -probleme - wiskundige modelle waarvan die vereistes gekenmerk word deur lineêre verwantskappe, d.w.s. bestaan uit 'n enkele doelwit verteenwoordig deur 'n lineêre vergelyking wat gemaksimeer of geminimaliseer moet word. Vir meer inligting, kyk asseblief na hierdie bladsy.
- Evolusionêr . Dit word gebruik vir nie-gladde probleme, wat die moeilikste tipe optimaliseringsprobleme is om op te los omdat sommige van die funksies nie-glad of selfs diskontinu is, en daarom is dit moeilik om die rigting te bepaal waarin 'n funksie toeneem of afneem. Vir meer inligting, sien asseblief hierdie bladsy.
Om te verander hoe Oplosser 'n oplossing vind, klik die Opsies -knoppie in die Oplosserparameters dialoogkassie, en konfigureer enige of alle opsies op die GRG Nielineêre , Alle Metodes en Evolusionêre -oortjies.
Dit is hoe jy Solver in Excel kan gebruik om die beste oplossings vir jou besluitprobleme te vind. En nou wil jy dalklaai die Excel Solver-voorbeelde af wat in hierdie tutoriaal bespreek word en herontwerp hulle vir beter begrip. Ek bedank jou vir die lees en hoop om jou volgende week op ons blog te sien.
jou help om die opbrengs van belegging te maksimeer, die optimale begroting vir jou advertensieveldtog te kies, die beste werkskedule vir jou werknemers te maak, die afleweringskoste te minimaliseer, ensovoorts.Hoe om Solver by Excel te voeg
Die Solver-byvoeging is ingesluit by alle weergawes van Microsoft Excel wat met 2003 begin, maar dit is nie by verstek geaktiveer nie.
Om Solver by jou Excel te voeg, voer die volgende stappe uit:
- In Excel 2010 - Excel 365, klik Lêer > Opsies .
Klik in Excel 2007 die Microsoft Office -knoppie, en klik dan Excel-opsies .
- In die Excel-opsies -dialoog, klik Byvoegings op die linkerkantbalk, maak seker Excel-byvoegings word gekies in die Bestuur -blokkie onderaan die venster, en klik Gaan .
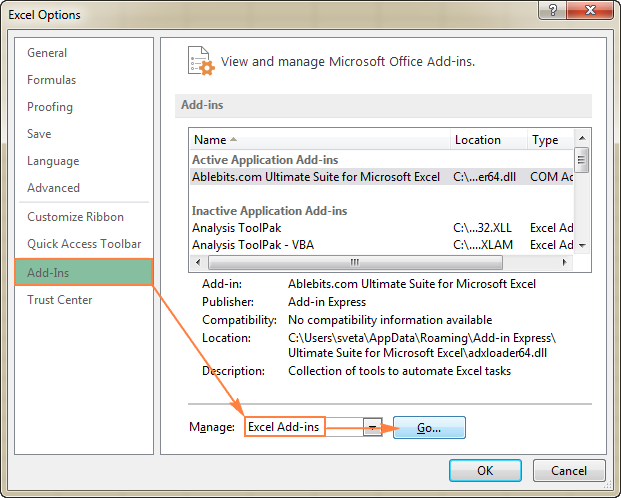
- In die Byvoegings dialoogkassie, merk die Oplosserbyvoeging boks en klik OK :
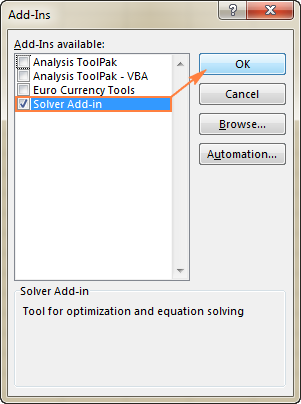
Om Solver op Excel 2003 te kry, gaan na die Tools -kieslys en klik Byvoegings . In die Byvoegings beskikbaar -lys, merk die Oplosserbyvoeging -blokkie en klik OK .
Let wel. As Excel 'n boodskap wys dat die Solver-byvoeging nie tans op jou rekenaar geïnstalleer is nie, klik Ja om dit te installeer.
Waar is Oplosser in Excel?
In die moderne weergawes van Excel verskyn die Oplosser -knoppie op die Data -oortjie, in die Analise groep:

Waar isOplosser in Excel 2003?
Nadat die Oplosser-byvoeging na Excel 2003 gelaai is, word sy opdrag by die Gereedskap -kieslys gevoeg:
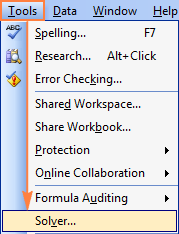
Nou dat jy weet waar om Solver in Excel te vind, maak 'n nuwe werkblad oop en kom ons begin!
Let wel. Die voorbeelde wat in hierdie tutoriaal bespreek word, gebruik Solver in Excel 2013. As jy 'n ander Excel-weergawe het, sal die skermkiekies dalk nie presies ooreenstem met jou weergawe nie, alhoewel die Solver-funksionaliteit basies dieselfde is.
Hoe om Solver in Excel te gebruik
Voordat die Excel Solver-byvoeging uitgevoer word, formuleer die model wat jy wil oplos in 'n werkblad. In hierdie voorbeeld, kom ons vind 'n oplossing vir die volgende eenvoudige optimaliseringsprobleem.
Probleem . Gestel jy is die eienaar van 'n skoonheidsalon en beplan om 'n nuwe diens aan jou kliënte te lewer. Hiervoor moet jy 'n nuwe toerusting koop wat $40 000 kos, wat binne 12 maande per paaiement betaal moet word.
Doelwit : Bereken die minimale koste per diens wat jou sal laat betaal vir die nuwe toerusting binne die gespesifiseerde tydraamwerk.
Vir hierdie taak het ek die volgende model geskep:
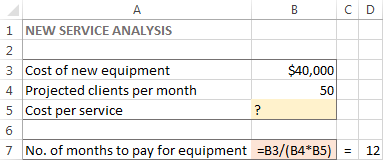
En nou, kom ons kyk hoe Excel Solver kan vind 'n oplossing vir hierdie probleem.
1. Begin Excel Solver
Op die Data -oortjie, in die Analise -groep, klik die Oplosser -knoppie.
2. Definieer die probleem
Die venster Oplosserparameters sal oopmaak waar jyom die 3 primêre komponente op te stel:
- Doelwitsel
- Veranderlike selle
- Beperkings
Presies waarmee doen Excel Solver bogenoemde parameters? Dit vind die optimale waarde (maksimum, minimum of gespesifiseer) vir die formule in die Objective -sel deur die waardes in die Veranderlike -selle te verander, en onderhewig aan beperkings in die Beperkings selle.
Doelwit
Die Doelwit -sel ( Teiken -sel in vroeëre Excel-weergawes) is die sel wat 'n formule bevat wat die doel, of doel, van die probleem verteenwoordig. Die doelwit kan wees om die een of ander teikenwaarde te maksimeer, te minimaliseer of te bereik.
In hierdie voorbeeld is die doelsel B7, wat die betalingstermyn bereken deur die formule =B3/(B4*B5) te gebruik en die resultaat van die formule moet gelyk wees aan 12:
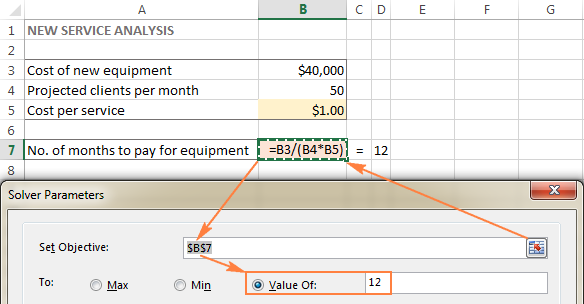
Veranderlike selle
Veranderlike selle ( Verander selle of Verstelbaar selle in vroeëre weergawes) is selle wat veranderlike data bevat wat verander kan word om die doelwit te bereik. Excel Solver laat toe om tot 200 veranderlike selle te spesifiseer.
In hierdie voorbeeld het ons 'n paar selle waarvan die waardes verander kan word:
- Geprojekteerde kliënte per maand (B4) wat moet minder as of gelyk aan 50 wees; en
- Koste per diens (B5) wat ons wil hê Excel Solver moet bereken.
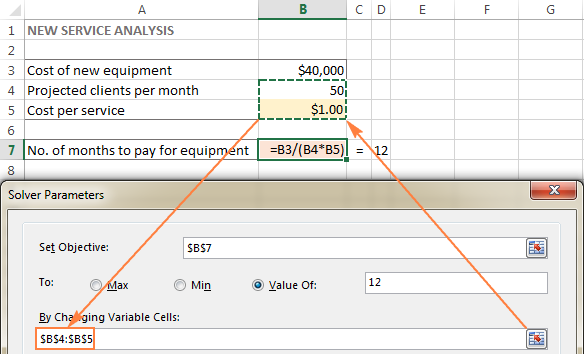
Wenk. As die veranderlike selle of reekse in jou model nie-aangrensend is,kies die eerste sel of reeks, en druk en hou dan die Ctrl-sleutel in terwyl jy ander selle en/of reekse kies. Of tik die reekse handmatig in, geskei met kommas.
Beperkings
Die Excel Oplosser Beperkings is beperkings of beperkings van die moontlike oplossings vir die probleem. Om dit anders te stel, beperkings is die voorwaardes waaraan voldoen moet word.
Om 'n beperking(e) by te voeg, doen die volgende:
- Klik die Voeg by knoppie regs na die " Onderworpe aan die beperkings "-boks.
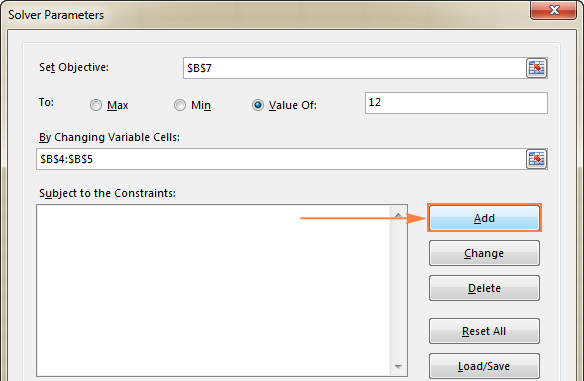
- In die Beperking -venster, voer 'n beperking in.
- Klik die Voeg by -knoppie om die beperking by die lys te voeg.
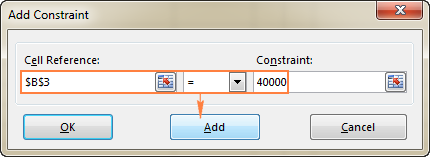
- Gaan voort ander beperkings in te voer.
- Nadat jy die finale beperking ingevoer het, klik OK om terug te keer na die hoofvenster Oplosser Parameters .
Excel Solver laat toe om die volgende verwantskappe tussen die verwysde sel en die beperking te spesifiseer.
- Kinder as of gelyk aan , gelyk aan , en groter as of gelyk aan . Jy stel hierdie verwantskappe deur 'n sel in die Selverwysing -kassie te kies en een van die volgende tekens te kies: <= , =, of > ;= , en tik dan 'n nommer, selverwysing/selnaam, of formule in die Beperking -blokkie (sien asseblief die skermkiekie hierbo).
- Geheelgetal . As die sel waarna verwys word 'n heelgetal moet wees, kies int ,en die woord heelgetal sal in die Beperking -blokkie verskyn.
- Verskillende waardes . As elke sel in die verwysingsreeks 'n ander waarde moet bevat, kies verskil , en die woord Alle verskil sal in die Beperking -blokkie verskyn.
- Binêr . As jy 'n verwysde sel tot 0 of 1 wil beperk, kies bin , en die woord binêr sal in die Beperking -boks verskyn.
Let wel. Die int , bin en dif verhoudings kan slegs gebruik word vir beperkings op Veranderlike selle.
Om 'n bestaande beperking te wysig of vee , doen die volgende:
- In die Oplosserparameters dialoogkassie, klik die beperking.
- Om die gekose beperking te wysig, klik Verander en maak die veranderinge wat jy wil hê.
- Om die beperking uit te vee, klik die Verwyder -knoppie .
In hierdie voorbeeld is die beperkings:
- B3=40000 - koste van die nuwe toerusting is $40,000.
- B4<=50 - die aantal geprojekteerde pasiënte per maand in minder as 50.
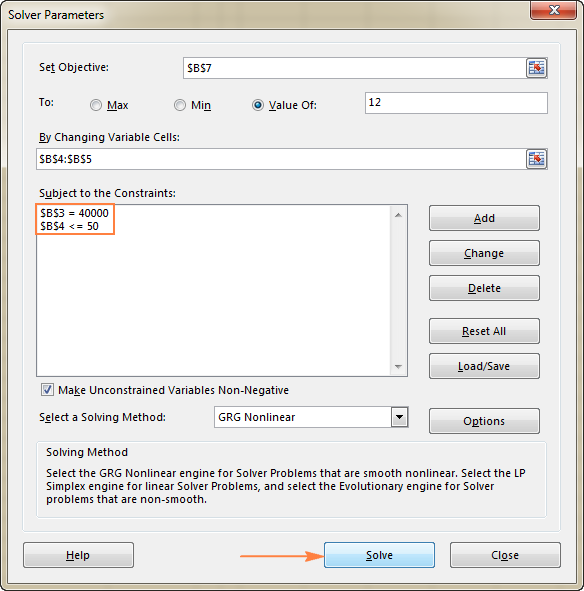
3. Los die probleem op
Nadat jy al die parameters opgestel het, klik die Los op -knoppie onderaan die Oplosparameters -venster (sien die skermkiekie hierbo) en laat die Excel Solver-byvoeging vind die optimale oplossing vir jou probleem.
Afhangende van die modelkompleksiteit, rekenaargeheue en verwerkerspoed, kan dit 'n paar neemsekondes, 'n paar minute of selfs 'n paar uur.
Wanneer Oplosser klaar verwerk het, sal dit die Oplosserresultate dialoogvenster vertoon, waar jy Behou die Oplosser Oplossing
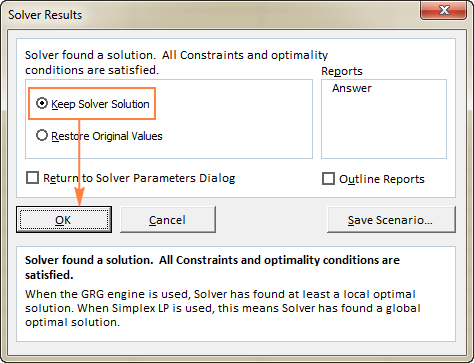
Die venster Oplosserresultaat sal toemaak en die oplossing sal verskyn dadelik op die werkblad.
In hierdie voorbeeld verskyn $66,67 in sel B5, wat die minimale koste per diens is wat jou in 12 maande vir die nuwe toerusting sal laat betaal, mits daar ten minste 50 kliënte per diens is. maand:
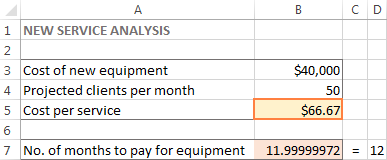
Wenke:
- As die Excel Oplosser 'n sekere probleem te lank verwerk het, kan jy die proses onderbreek deur die Esc sleutel. Excel sal die werkblad herbereken met die laaste waardes wat vir die Veranderlike -selle gevind is.
- Om meer besonderhede oor die opgeloste probleem te kry, klik 'n verslagtipe in die Verslae -kassie , en klik dan OK . Die verslag sal op 'n nuwe werkblad geskep word:
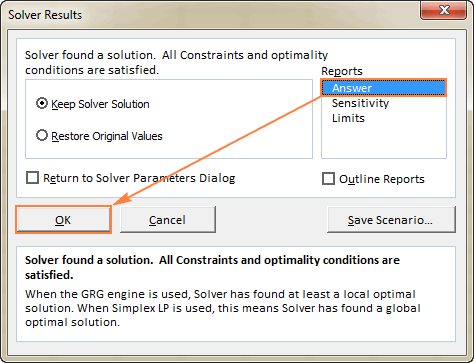
Nou dat jy die basiese idee het van hoe om Solver in Excel te gebruik, kom ons kyk na 'n paar van naderby meer voorbeelde wat jou kan help om meer begrip te kry.
Excel Solver-voorbeelde
Hieronder vind jy nog twee voorbeelde van die gebruik van die Excel Solver-byvoeging. Eerstens sal ons 'n oplossing vind vir 'n bekende legkaart, en dan 'n werklike lineêre programmeringsprobleem oplos.
Excel Solver voorbeeld 1 (magic square)
Iglo almal is bekend met "magic square" legkaarte waar jy 'n stel getalle in 'n vierkant moet plaas sodat alle rye, kolomme en hoeklyne 'n sekere getal optel.
Ken jy byvoorbeeld 'n oplossing vir die 3x3-vierkant wat getalle van 1 tot 9 bevat waar elke ry, kolom en diagonaal 15 optel?
Dit is waarskynlik nie 'n groot probleem om hierdie legkaart deur proef en fout op te los nie, maar ek wed dat die Oplosser sal vind die oplossing vinniger. Ons deel van die taak is om die probleem behoorlik te definieer.
Tik om mee te begin die nommers van 1 tot 9 in 'n tabel wat uit 3 rye en 3 kolomme bestaan. Die Excel Solver het nie eintlik daardie nommers nodig nie, maar hulle sal ons help om die probleem te visualiseer. Wat die Excel Solver-byvoeging regtig nodig het, is die SOM-formules wat elke ry, kolom en 2 hoeklyne tel:
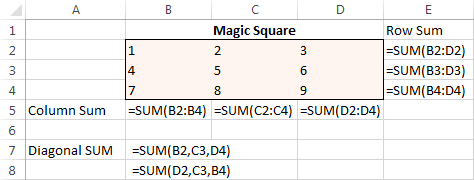
Met al die formules in plek, hardloop Solver en stel op die volgende parameters:
- Stel Objective . In hierdie voorbeeld hoef ons geen doelwit te stel nie, so laat hierdie blokkie leeg.
- Veranderlike selle . Ons wil getalle in selle B2 tot D4 vul, dus kies die reeks B2:D4.
- Beperkings . Die volgende voorwaardes moet nagekom word:
- $B$2:$D$4 = AllDifferent - al die Veranderlike selle moet verskillende waardes bevat.
- $B$2:$D$4 = heelgetal - almal van die Veranderlike selle moet heelgetalle wees.
- $B$5:$D$5 = 15 - die som van waardes in elkkolom moet gelyk wees aan 15.
- $E$2:$E$4 = 15 - die som van waardes in elke ry moet gelyk wees aan 15.
- $B$7:$B$8 = 15 - die som van beide hoeklyne moet gelyk wees aan 15.
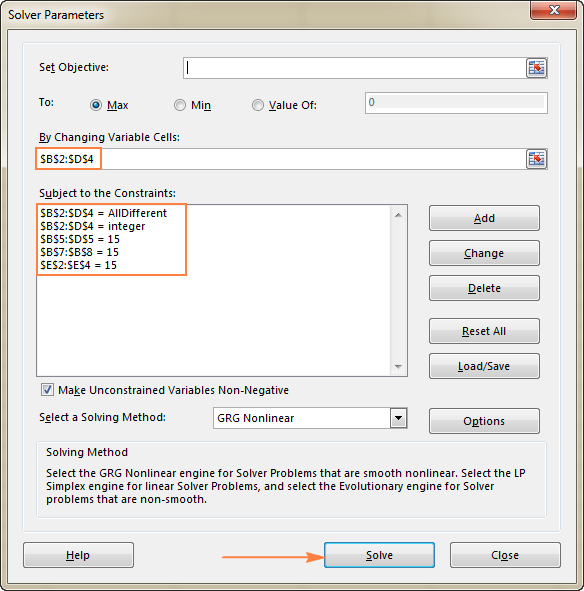
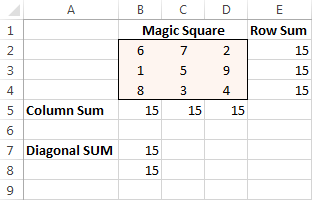
Klik laastens die Los op -knoppie, en die oplossing is daar!
Excel Solver voorbeeld 2 (lineêre programmeringsprobleem)
Dit is 'n voorbeeld van 'n eenvoudige vervoeroptimeringsprobleem met 'n lineêre doelwit. Meer komplekse optimaliseringsmodelle van hierdie soort word deur baie maatskappye gebruik om duisende dollars elke jaar te bespaar.
Probleem : Jy wil die koste van die versending van goedere van 2 verskillende pakhuise tot 4 verskillende verminder. kliënte. Elke pakhuis het 'n beperkte aanbod en elke kliënt het 'n sekere vraag.
Doelwit : Minimaliseer die totale verskepingskoste, wat nie die hoeveelheid beskikbaar by elke pakhuis oorskry nie, en voldoen aan die vraag van elke klant .
Brondata
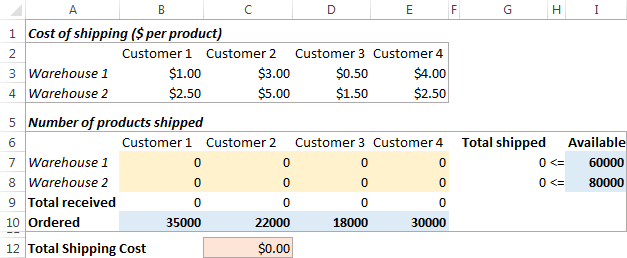
Hier is hoe ons vervoeroptimeringsprobleem lyk:
Formulering van die model
Om definieer ons lineêre programmeringsprobleem vir die Excel Solver, kom ons beantwoord die 3 hoofvrae:
- Watter besluite moet geneem word? Ons wil die optimale hoeveelheid goedere bereken om aan elke klant uit elke pakhuis te lewer. Dit is Veranderlike selle (B7:E8).
- Wat is die beperkings? Die voorrade beskikbaar by elke pakhuis (I7:I8) kan nie oorskry word nie, en die

