Πίνακας περιεχομένων
Το σεμινάριο εξηγεί πώς να προσθέσετε και πού να βρείτε το Solver σε διάφορες εκδόσεις του Excel, από το 2016 έως το 2003. Βήμα προς βήμα παραδείγματα δείχνουν πώς να χρησιμοποιήσετε το Excel Solver για να βρείτε βέλτιστες λύσεις για γραμμικό προγραμματισμό και άλλα είδη προβλημάτων.
Όλοι γνωρίζουν ότι το Microsoft Excel περιέχει πολλές χρήσιμες συναρτήσεις και ισχυρά εργαλεία που μπορούν να σας γλιτώσουν από ώρες υπολογισμών. Γνωρίζατε όμως ότι διαθέτει επίσης ένα εργαλείο που μπορεί να σας βοηθήσει να βρείτε τις βέλτιστες λύσεις για προβλήματα αποφάσεων;
Σε αυτό το σεμινάριο, θα καλύψουμε όλες τις βασικές πτυχές του πρόσθετου Excel Solver και θα σας δώσουμε έναν βήμα προς βήμα οδηγό για το πώς να το χρησιμοποιήσετε πιο αποτελεσματικά.
Τι είναι το Excel Solver;
Excel Solver ανήκει σε ένα ειδικό σύνολο εντολών που συχνά αναφέρονται ως Εργαλεία Ανάλυσης Τι-αν. Προορίζεται κυρίως για την προσομοίωση και τη βελτιστοποίηση διαφόρων επιχειρηματικών και μηχανολογικών μοντέλων.
Το πρόσθετο Excel Solver είναι ιδιαίτερα χρήσιμο για την επίλυση προβλημάτων γραμμικού προγραμματισμού, ή αλλιώς προβλημάτων γραμμικής βελτιστοποίησης, και ως εκ τούτου μερικές φορές ονομάζεται λύτης γραμμικού προγραμματισμού Εκτός από αυτό, μπορεί να χειριστεί ομαλά μη γραμμικά και μη ομαλά προβλήματα. Για περισσότερες λεπτομέρειες, ανατρέξτε στην ενότητα αλγόριθμοι του Excel Solver.
Αν και το Solver δεν μπορεί να λύσει κάθε πιθανό πρόβλημα, είναι πραγματικά χρήσιμο όταν αντιμετωπίζετε όλα τα είδη προβλημάτων βελτιστοποίησης όπου πρέπει να πάρετε την καλύτερη δυνατή απόφαση. Για παράδειγμα, μπορεί να σας βοηθήσει να μεγιστοποιήσετε την απόδοση της επένδυσης, να επιλέξετε τον βέλτιστο προϋπολογισμό για τη διαφημιστική σας καμπάνια, να φτιάξετε το καλύτερο πρόγραμμα εργασίας για τους υπαλλήλους σας, να ελαχιστοποιήσετε το κόστος παράδοσης κ.ο.κ.
Πώς να προσθέσετε τον Solver στο Excel
Το πρόσθετο Solver περιλαμβάνεται σε όλες τις εκδόσεις του Microsoft Excel, αρχής γενομένης από το 2003, αλλά δεν είναι ενεργοποιημένο από προεπιλογή.
Για να προσθέσετε το Solver στο Excel, εκτελέστε τα ακόλουθα βήματα:
- Στο Excel 2010 - Excel 365, κάντε κλικ στο Αρχείο >, Επιλογές .
Στο Excel 2007, κάντε κλικ στο Microsoft Office και στη συνέχεια κάντε κλικ στο κουμπί Επιλογές Excel .
- Στο Επιλογές Excel διαλόγου, κάντε κλικ στο Add-Ins στην αριστερή πλαϊνή μπάρα, βεβαιωθείτε ότι Πρόσθετα του Excel είναι επιλεγμένο στο Διαχείριση στο κάτω μέρος του παραθύρου και κάντε κλικ στο κουμπί Go .
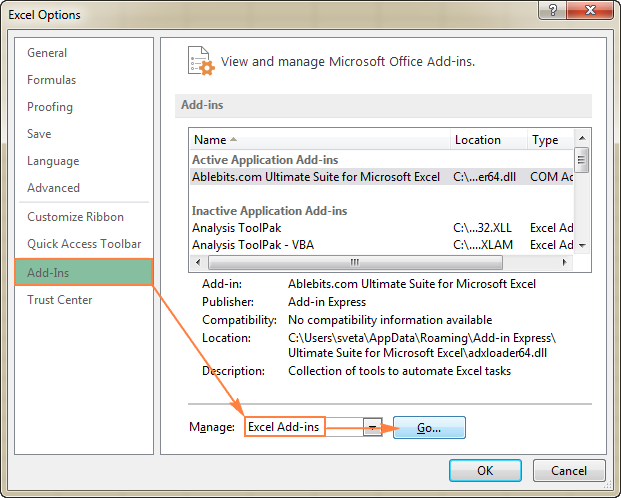
- Στο Add-Ins παράθυρο διαλόγου, επιλέξτε το Προσθήκη Solver και κάντε κλικ στο κουμπί OK :
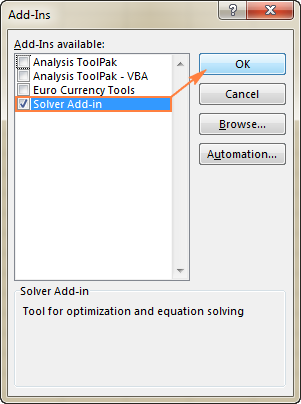
Για να ενεργοποιήσετε το Solver Excel 2003 , πηγαίνετε στο Εργαλεία και κάντε κλικ στο κουμπί Add-Ins . Στο Add-Ins διαθέσιμο λίστα, ελέγξτε το Προσθήκη Solver και κάντε κλικ στο κουμπί OK .
Σημείωση. Εάν το Excel εμφανίσει ένα μήνυμα ότι το πρόσθετο Solver δεν είναι εγκατεστημένο στον υπολογιστή σας, κάντε κλικ στο κουμπί Ναι για να το εγκαταστήσετε.
Πού βρίσκεται ο Solver στο Excel;
Στις σύγχρονες εκδόσεις του Excel, το Solver εμφανίζεται στο κουμπί Δεδομένα στην καρτέλα Ανάλυση ομάδα:

Πού βρίσκεται ο Solver στο Excel 2003;
Αφού φορτωθεί το Solver Add-in στο Excel 2003, η εντολή του προστίθεται στην ενότητα Εργαλεία μενού:
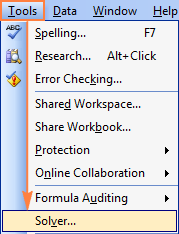
Τώρα που ξέρετε πού θα βρείτε το Solver στο Excel, ανοίξτε ένα νέο φύλλο εργασίας και ας ξεκινήσουμε!
Σημείωση. Τα παραδείγματα που αναλύονται σε αυτό το σεμινάριο χρησιμοποιούν το Solver στο Excel 2013. Αν έχετε άλλη έκδοση του Excel, τα στιγμιότυπα οθόνης μπορεί να μην ταιριάζουν ακριβώς με την έκδοσή σας, αν και η λειτουργικότητα του Solver είναι βασικά η ίδια.
Πώς να χρησιμοποιήσετε τον Solver στο Excel
Πριν εκτελέσετε το πρόσθετο Excel Solver, διατυπώστε το μοντέλο που θέλετε να επιλύσετε σε ένα φύλλο εργασίας. Σε αυτό το παράδειγμα, ας βρούμε μια λύση για το ακόλουθο απλό πρόβλημα βελτιστοποίησης.
Πρόβλημα Έστω ότι είστε ιδιοκτήτης ενός κομμωτηρίου ομορφιάς και σκοπεύετε να παρέχετε μια νέα υπηρεσία στους πελάτες σας. Για το σκοπό αυτό, πρέπει να αγοράσετε έναν νέο εξοπλισμό που κοστίζει 40.000 δολάρια, τα οποία θα πρέπει να καταβληθούν με δόσεις εντός 12 μηνών.
Στόχος : Υπολογίστε το ελάχιστο κόστος ανά υπηρεσία που θα σας επιτρέψει να εξοφλήσετε τον νέο εξοπλισμό εντός του καθορισμένου χρονικού πλαισίου.
Για την εργασία αυτή, δημιούργησα το ακόλουθο μοντέλο:
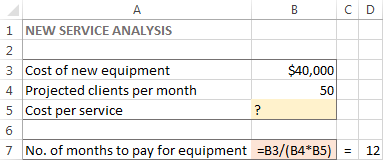
Και τώρα, ας δούμε πώς το Excel Solver μπορεί να βρει λύση για αυτό το πρόβλημα.
1. Εκτελέστε το Excel Solver
Στο Δεδομένα στην καρτέλα Ανάλυση ομάδα, κάντε κλικ στο Solver κουμπί.
2. Ορισμός του προβλήματος
Το Παράμετροι επιλύτη θα ανοίξει το παράθυρο όπου θα πρέπει να ρυθμίσετε τα 3 κύρια στοιχεία:
- Κελί στόχου
- Μεταβλητά κύτταρα
- Περιορισμοί
Τι ακριβώς κάνει το Excel Solver με τις παραπάνω παραμέτρους; Βρίσκει τη βέλτιστη τιμή (μέγιστη, ελάχιστη ή καθορισμένη) για τον τύπο στο πεδίο Στόχος αλλάζοντας τις τιμές στο πεδίο Μεταβλητή κύτταρα, και με την επιφύλαξη των περιορισμών της Περιορισμοί κύτταρα.
Στόχος
Το Στόχος κελί ( Στόχος κελί σε προηγούμενες εκδόσεις του Excel) είναι το κελί που περιέχει έναν τύπο Ο στόχος μπορεί να είναι η μεγιστοποίηση, η ελαχιστοποίηση ή η επίτευξη κάποιας τιμής-στόχου.
Σε αυτό το παράδειγμα, το αντικειμενικό κελί είναι το Β7, το οποίο υπολογίζει τον όρο πληρωμής χρησιμοποιώντας τον τύπο =B3/(B4*B5) και το αποτέλεσμα του τύπου θα πρέπει να είναι ίσο με 12:
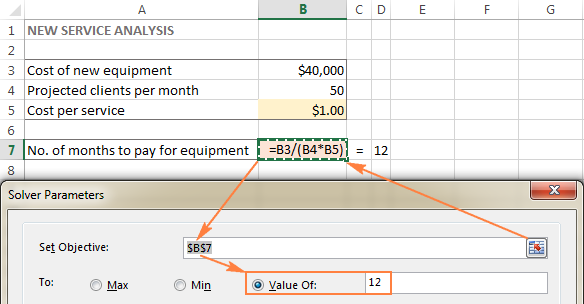
Μεταβλητά κύτταρα
Μεταβλητή κύτταρα ( Αλλαγή κύτταρα ή Ρυθμιζόμενο κελιά σε προηγούμενες εκδόσεις) είναι κελιά που περιέχουν μεταβλητά δεδομένα τα οποία μπορούν να αλλάξουν για την επίτευξη του στόχου. Το Excel Solver επιτρέπει τον προσδιορισμό έως και 200 μεταβλητών κελιών.
Σε αυτό το παράδειγμα, έχουμε μερικά κελιά των οποίων οι τιμές μπορούν να αλλάξουν:
- Προβλεπόμενοι πελάτες ανά μήνα (Β4) που πρέπει να είναι μικρότεροι ή ίσοι με 50- και
- Κόστος ανά υπηρεσία (B5) που θέλουμε να υπολογίσει το Excel Solver.
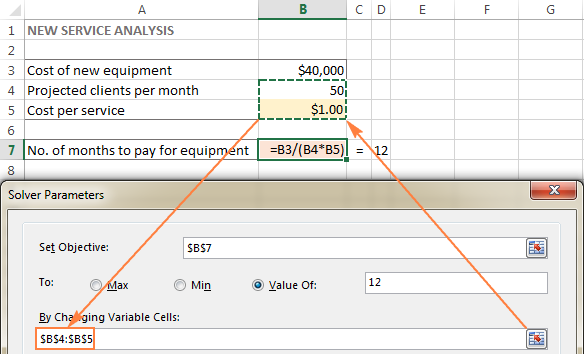
Συμβουλή. Εάν τα μεταβλητά κελιά ή οι περιοχές στο μοντέλο σας είναι μη παρακείμενα , επιλέξτε το πρώτο κελί ή την πρώτη περιοχή και, στη συνέχεια, πατήστε και κρατήστε πατημένο το πλήκτρο Ctrl ενώ επιλέγετε άλλα κελιά ή/και περιοχές. Ή, πληκτρολογήστε τις περιοχές χειροκίνητα, χωρισμένες με κόμμα.
Περιορισμοί
Το Excel Solver Περιορισμοί είναι περιορισμοί ή όρια των πιθανών λύσεων του προβλήματος. Για να το θέσουμε διαφορετικά, οι περιορισμοί είναι οι συνθήκες που πρέπει να πληρούνται.
Για να προσθέσετε έναν ή περισσότερους περιορισμούς, κάντε τα εξής:
- Κάντε κλικ στο Προσθέστε δεξιά στο κουμπί " Με την επιφύλαξη των περιορισμών " box.
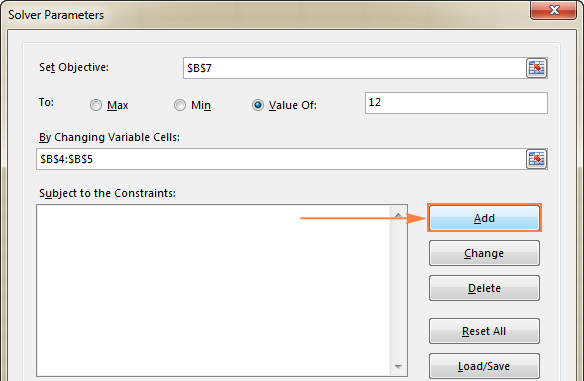
- Στο Περιορισμός εισάγετε έναν περιορισμό.
- Κάντε κλικ στο Προσθέστε για να προσθέσετε τον περιορισμό στη λίστα.
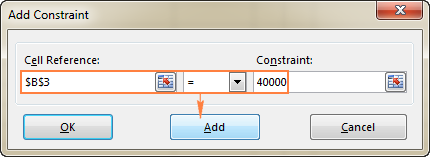
- Συνεχίστε να εισάγετε άλλους περιορισμούς.
- Αφού εισαγάγετε τον τελικό περιορισμό, κάντε κλικ στο κουμπί OK για να επιστρέψετε στην κύρια Solver Παράμετροι παράθυρο.
Το Excel Solver επιτρέπει τον προσδιορισμό των ακόλουθων σχέσεων μεταξύ του κελιού στο οποίο γίνεται αναφορά και του περιορισμού.
- Λιγότερο ή ίσο με , ίση με , και μεγαλύτερη ή ίση με Ορίζετε αυτές τις σχέσεις επιλέγοντας ένα κελί στο Αναφορά κυττάρου επιλέγοντας ένα από τα ακόλουθα σύμβολα: <= , =, ή >= και στη συνέχεια πληκτρολογώντας έναν αριθμό, αναφορά κελιού / όνομα κελιού ή τύπο στο πεδίο Περιορισμός (δείτε το παραπάνω στιγμιότυπο οθόνης).
- Ακέραιος αριθμός Εάν το κελί στο οποίο γίνεται αναφορά πρέπει να είναι ακέραιος αριθμός, επιλέξτε int , και η λέξη integer θα εμφανιστεί στο Περιορισμός κουτί.
- Διαφορετικές τιμές Αν κάθε κελί στην περιοχή αναφοράς πρέπει να περιέχει διαφορετική τιμή, επιλέξτε dif , και η λέξη AllDifferent θα εμφανιστεί στο Περιορισμός κουτί.
- Δυαδικό Αν θέλετε να περιορίσετε ένα αναφερόμενο κελί είτε στο 0 είτε στο 1, επιλέξτε bin , και η λέξη δυαδικό θα εμφανιστεί στο Περιορισμός κουτί.
Σημείωση. int , bin , και dif μπορούν να χρησιμοποιηθούν μόνο για περιορισμούς σε κελιά Μεταβλητών.
Προς επεξεργασία ή delete έναν υπάρχοντα περιορισμό κάνετε τα εξής:
- Στο Παράμετροι επιλύτη παράθυρο διαλόγου, κάντε κλικ στον περιορισμό.
- Για να τροποποιήσετε τον επιλεγμένο περιορισμό, κάντε κλικ στο Αλλαγή και κάντε τις αλλαγές που θέλετε.
- Για να διαγράψετε τον περιορισμό, κάντε κλικ στο Διαγραφή κουμπί.
Σε αυτό το παράδειγμα, οι περιορισμοί είναι:
- B3=40000 - το κόστος του νέου εξοπλισμού είναι 40.000 δολάρια.
- B4<=50 - ο αριθμός των προβλεπόμενων ασθενών ανά μήνα σε λιγότερο από 50.
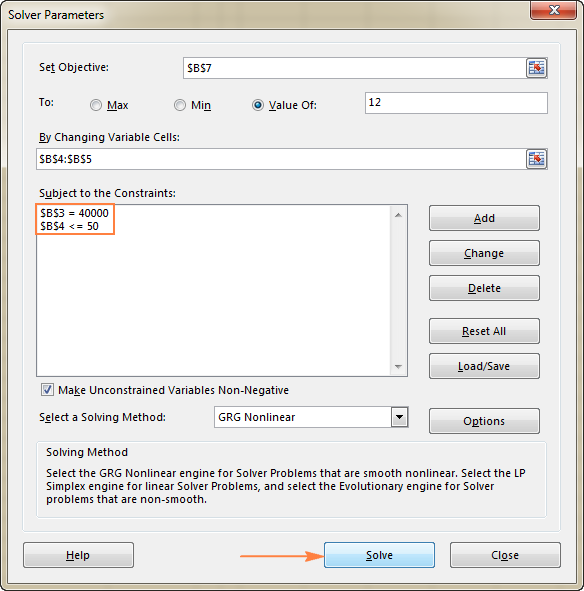
3. Επίλυση του προβλήματος
Αφού ρυθμίσετε όλες τις παραμέτρους, κάντε κλικ στο κουμπί Λύστε το στο κάτω μέρος της οθόνης Παράμετροι επιλύτη παράθυρο (βλ. το παραπάνω στιγμιότυπο οθόνης) και αφήστε το πρόσθετο Excel Solver να βρει τη βέλτιστη λύση για το πρόβλημά σας.
Ανάλογα με την πολυπλοκότητα του μοντέλου, τη μνήμη του υπολογιστή και την ταχύτητα του επεξεργαστή, μπορεί να χρειαστούν μερικά δευτερόλεπτα, μερικά λεπτά ή ακόμη και μερικές ώρες.
Όταν ο Solver ολοκληρώσει την επεξεργασία, θα εμφανίσει το Αποτελέσματα Solver παράθυρο διαλόγου, όπου επιλέγετε Διατηρήστε τη λύση Solver και κάντε κλικ στο OK :
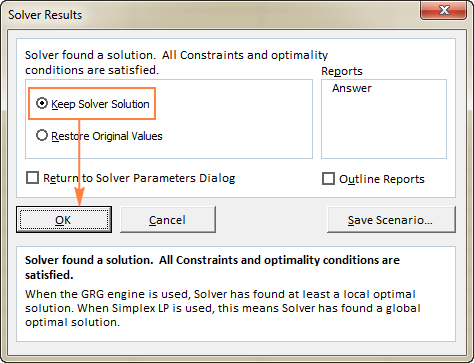
Το Αποτέλεσμα Solver το παράθυρο θα κλείσει και η λύση θα εμφανιστεί αμέσως στο φύλλο εργασίας.
Σε αυτό το παράδειγμα, στο κελί Β5 εμφανίζονται 66,67 δολάρια, το οποίο είναι το ελάχιστο κόστος ανά υπηρεσία που θα σας επιτρέψει να εξοφλήσετε τον νέο εξοπλισμό σε 12 μήνες, υπό την προϋπόθεση ότι υπάρχουν τουλάχιστον 50 πελάτες ανά μήνα:
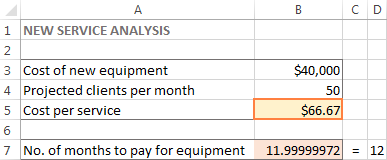
Συμβουλές:
- Εάν ο Excel Solver επεξεργάζεται ένα συγκεκριμένο πρόβλημα για πολύ ώρα, μπορείτε να διακόψετε τη διαδικασία πατώντας το πλήκτρο Esc. Το Excel θα υπολογίσει εκ νέου το φύλλο εργασίας με τις τελευταίες τιμές που βρέθηκαν για το Μεταβλητή κύτταρα.
- Για να λάβετε περισσότερες λεπτομέρειες σχετικά με το πρόβλημα που επιλύθηκε, κάντε κλικ σε έναν τύπο αναφοράς στην ενότητα Αναφορές και, στη συνέχεια, κάντε κλικ στο OK Η έκθεση θα δημιουργηθεί σε ένα νέο φύλλο εργασίας:
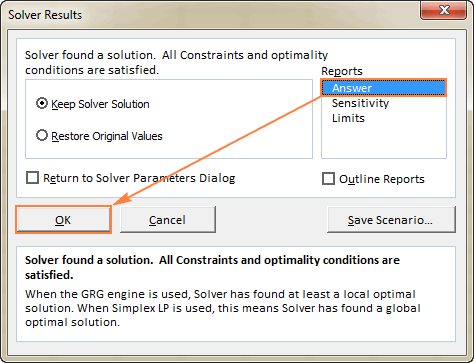
Τώρα που έχετε αποκτήσει τη βασική ιδέα για τον τρόπο χρήσης του Solver στο Excel, ας δούμε αναλυτικότερα μερικά ακόμη παραδείγματα που μπορεί να σας βοηθήσουν να κατανοήσετε καλύτερα.
Παραδείγματα Excel Solver
Παρακάτω θα βρείτε δύο ακόμη παραδείγματα χρήσης του πρόσθετου Excel Solver. Πρώτον, θα βρούμε τη λύση ενός γνωστού γρίφου και, στη συνέχεια, θα λύσουμε ένα πραγματικό πρόβλημα γραμμικού προγραμματισμού.
Παράδειγμα Excel Solver 1 (μαγικό τετράγωνο)
Πιστεύω ότι όλοι είναι εξοικειωμένοι με τους γρίφους "μαγικό τετράγωνο", όπου πρέπει να τοποθετήσετε ένα σύνολο αριθμών σε ένα τετράγωνο έτσι ώστε όλες οι γραμμές, οι στήλες και οι διαγώνιοι να αθροίζουν έναν συγκεκριμένο αριθμό.
Για παράδειγμα, γνωρίζετε μια λύση για το τετράγωνο 3x3 που περιέχει αριθμούς από το 1 έως το 9, όπου κάθε γραμμή, στήλη και διαγώνιος αθροίζει 15;
Πιθανώς δεν είναι μεγάλη υπόθεση να λύσετε αυτό το παζλ με δοκιμή και λάθος, αλλά στοιχηματίζω ότι ο Solver θα βρει τη λύση πιο γρήγορα. Το δικό μας μέρος της δουλειάς είναι να ορίσουμε σωστά το πρόβλημα.
Αρχικά, εισάγετε τους αριθμούς από το 1 έως το 9 σε έναν πίνακα που αποτελείται από 3 γραμμές και 3 στήλες. Το Excel Solver δεν χρειάζεται στην πραγματικότητα αυτούς τους αριθμούς, αλλά θα μας βοηθήσουν να οπτικοποιήσουμε το πρόβλημα. Αυτό που πραγματικά χρειάζεται το πρόσθετο Excel Solver είναι οι τύποι SUM που αθροίζουν κάθε γραμμή, στήλη και 2 διαγώνιες:
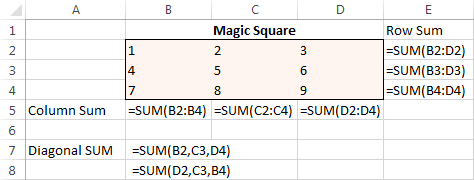
Με όλους τους τύπους στη θέση τους, εκτελέστε το Solver και ρυθμίστε τις ακόλουθες παραμέτρους:
- Ορίστε Στόχος Σε αυτό το παράδειγμα, δεν χρειάζεται να ορίσουμε κάποιον στόχο, οπότε αφήστε αυτό το πλαίσιο κενό.
- Μεταβλητά κύτταρα Θέλουμε να συμπληρώσουμε αριθμούς στα κελιά B2 έως D4, οπότε επιλέγουμε την περιοχή B2:D4.
- Περιορισμοί Πρέπει να πληρούνται οι ακόλουθες προϋποθέσεις:
- $B$2:$D$4 = AllDifferent - όλα τα κελιά Variable θα πρέπει να περιέχουν διαφορετικές τιμές.
- $B$2:$D$4 = integer - όλα τα κελιά Variable πρέπει να είναι ακέραιοι αριθμοί.
- $B$5:$D$5 = 15 - το άθροισμα των τιμών σε κάθε στήλη πρέπει να ισούται με 15.
- $E$2:$E$4 = 15 - το άθροισμα των τιμών σε κάθε γραμμή πρέπει να ισούται με 15.
- $B$7:$B$8 = 15 - το άθροισμα των δύο διαγωνίων πρέπει να ισούται με 15.
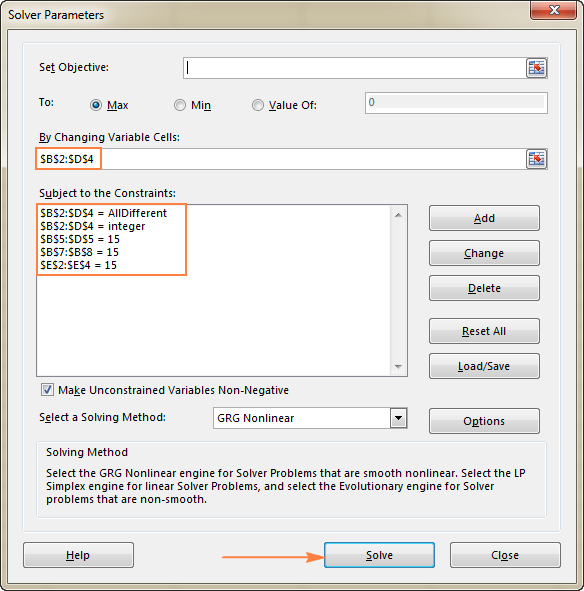
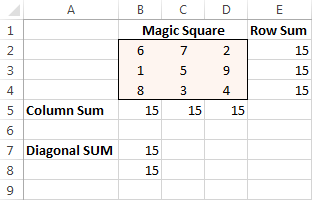
Τέλος, κάντε κλικ στο Λύστε το και η λύση είναι εκεί!
Excel Solver παράδειγμα 2 (πρόβλημα γραμμικού προγραμματισμού)
Αυτό είναι ένα παράδειγμα ενός απλού προβλήματος βελτιστοποίησης μεταφορών με γραμμικό στόχο. Πιο σύνθετα μοντέλα βελτιστοποίησης αυτού του είδους χρησιμοποιούνται από πολλές εταιρείες για την εξοικονόμηση χιλιάδων δολαρίων κάθε χρόνο.
Πρόβλημα : Θέλετε να ελαχιστοποιήσετε το κόστος αποστολής αγαθών από 2 διαφορετικές αποθήκες σε 4 διαφορετικούς πελάτες. Κάθε αποθήκη έχει περιορισμένη προσφορά και κάθε πελάτης έχει συγκεκριμένη ζήτηση.
Στόχος : Ελαχιστοποίηση του συνολικού κόστους αποστολής, μη υπερβαίνοντας την ποσότητα που είναι διαθέσιμη σε κάθε αποθήκη και ικανοποιώντας τη ζήτηση κάθε πελάτη.
Δεδομένα πηγής
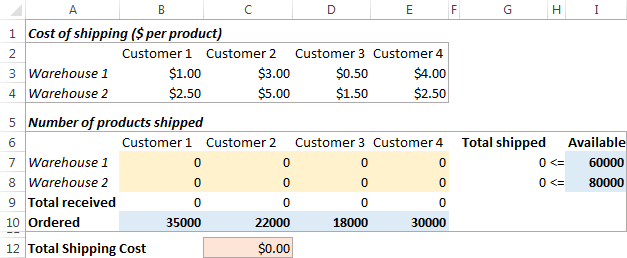
Να πώς μοιάζει το πρόβλημα βελτιστοποίησης της μεταφοράς μας:
Διατύπωση του μοντέλου
Για να ορίσουμε το πρόβλημα γραμμικού προγραμματισμού για το Excel Solver, ας απαντήσουμε στις 3 κύριες ερωτήσεις:
- Ποιες αποφάσεις πρέπει να ληφθούν; Θέλουμε να υπολογίσουμε τη βέλτιστη ποσότητα αγαθών που πρέπει να παραδώσουμε σε κάθε πελάτη από κάθε αποθήκη. Αυτές είναι οι εξής Μεταβλητή κύτταρα (B7:E8).
- Ποιοι είναι οι περιορισμοί; Οι διαθέσιμες προμήθειες σε κάθε αποθήκη (I7:I8) δεν μπορούν να υπερβούν και η ποσότητα που παραγγέλνει κάθε πελάτης (B10:E10) πρέπει να παραδοθεί. Οι περιορισμοί αυτοί είναι οι εξής Περιορισμένη κύτταρα .
- Ποιος είναι ο στόχος; Το ελάχιστο συνολικό κόστος αποστολής. Και αυτό είναι το Στόχος κύτταρο (C12).
Το επόμενο πράγμα που πρέπει να κάνετε είναι να υπολογίσετε τη συνολική ποσότητα που αποστέλλεται από κάθε αποθήκη (G7:G8) και το σύνολο των αγαθών που παραλαμβάνονται από κάθε πελάτη (B9:E9). Μπορείτε να το κάνετε αυτό με απλούς τύπους Sum που παρουσιάζονται στο παρακάτω στιγμιότυπο οθόνης. Επίσης, εισάγετε τον τύπο SUMPRODUCT στο C12 για να υπολογίσετε το συνολικό κόστος αποστολής:
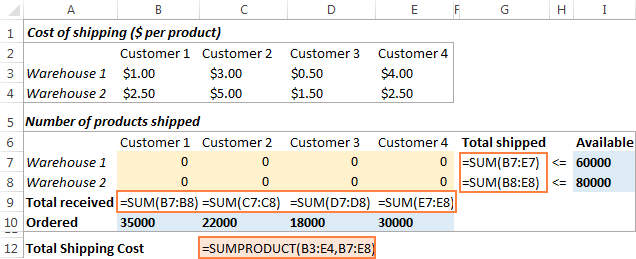
Για να γίνει πιο κατανοητό το μοντέλο βελτιστοποίησης μεταφορών, δημιουργήστε τις ακόλουθες ονομαστικές περιοχές:
| Όνομα περιοχής | Κύτταρα | Παράμετρος επιλύτη |
| Προϊόντα_αποσταλμένα | B7:E8 | Μεταβλητά κύτταρα |
| Διαθέσιμο | I7:I8 | Περιορισμός |
| Total_shipped | G7:G8 | Περιορισμός |
| Παραγγελία | B10:E10 | Περιορισμός |
| Σύνολο_παραληφθέντων | B9:E9 | Περιορισμός |
| Shipping_cost | C12 | Στόχος |
Το τελευταίο πράγμα που απομένει να κάνετε είναι να ρυθμίσετε τις παραμέτρους του Excel Solver:
- Στόχος: Shipping_cost σε Min
- Μεταβλητά κύτταρα: Products_shipped
- Περιορισμοί: Total_received = Ordered και Total_shipped <= Available
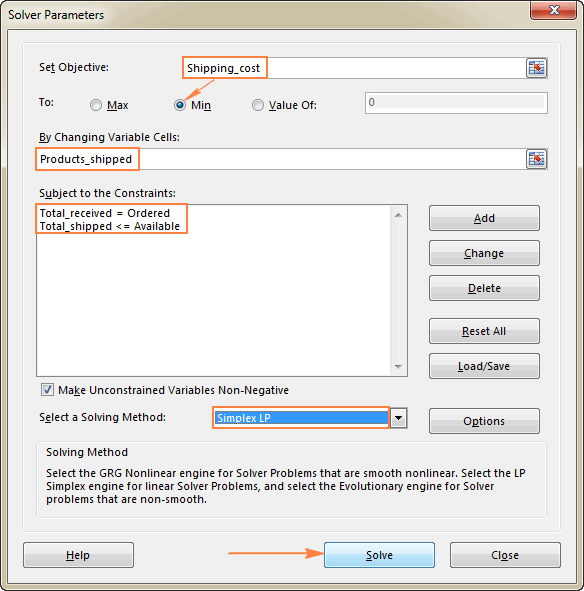
Παρακαλούμε προσέξτε ότι έχουμε επιλέξει το Simplex LP μέθοδο επίλυσης σε αυτό το παράδειγμα, επειδή έχουμε να κάνουμε με το πρόβλημα του γραμμικού προγραμματισμού. Αν δεν είστε σίγουροι για το είδος του προβλήματος που σας απασχολεί, μπορείτε να αφήσετε την προεπιλεγμένη επιλογή GRG Μη γραμμική Για περισσότερες πληροφορίες, ανατρέξτε στην ενότητα αλγόριθμοι του Excel Solver.
Λύση
Κάντε κλικ στο Λύστε το στο κάτω μέρος της οθόνης Παράμετροι επιλύτη και θα λάβετε την απάντησή σας. Σε αυτό το παράδειγμα, το πρόσθετο Excel Solver υπολόγισε τη βέλτιστη ποσότητα αγαθών που πρέπει να παραδοθεί σε κάθε πελάτη από κάθε αποθήκη με το ελάχιστο συνολικό κόστος αποστολής:
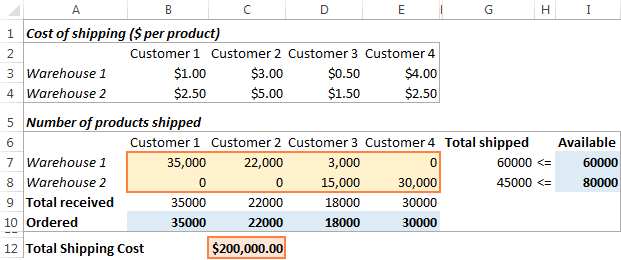
Πώς να αποθηκεύετε και να φορτώνετε σενάρια του Excel Solver
Κατά την επίλυση ενός συγκεκριμένου μοντέλου, μπορεί να θέλετε να αποθηκεύσετε το Μεταβλητή τιμές των κελιών ως σενάριο που μπορείτε να δείτε ή να επαναχρησιμοποιήσετε αργότερα.
Για παράδειγμα, κατά τον υπολογισμό του ελάχιστου κόστους υπηρεσιών στο πρώτο παράδειγμα που αναλύεται σε αυτό το σεμινάριο, ίσως θελήσετε να δοκιμάσετε διαφορετικούς αριθμούς προβλεπόμενων πελατών ανά μήνα και να δείτε πώς αυτό επηρεάζει το κόστος υπηρεσιών. Σε αυτό το σημείο, ίσως θελήσετε να αποθηκεύσετε το πιο πιθανό σενάριο που έχετε ήδη υπολογίσει και να το επαναφέρετε ανά πάσα στιγμή.
Εξοικονόμηση ένα σενάριο του Excel Solver καταλήγει στην επιλογή μιας περιοχής κελιών για την αποθήκευση των δεδομένων. Φόρτωση ενός μοντέλου Solver είναι απλώς θέμα παροχής στο Excel της περιοχής κελιών όπου έχει αποθηκευτεί το μοντέλο σας. Τα λεπτομερή βήματα ακολουθούν παρακάτω.
Αποθήκευση του μοντέλου
Για να αποθηκεύσετε το σενάριο του Excel Solver, εκτελέστε τα ακόλουθα βήματα:
- Ανοίξτε το φύλλο εργασίας με το υπολογισμένο μοντέλο και εκτελέστε το Excel Solver.
- Στο Παράμετροι επιλύτη παράθυρο, κάντε κλικ στο Φόρτωση/αποθήκευση κουμπί.
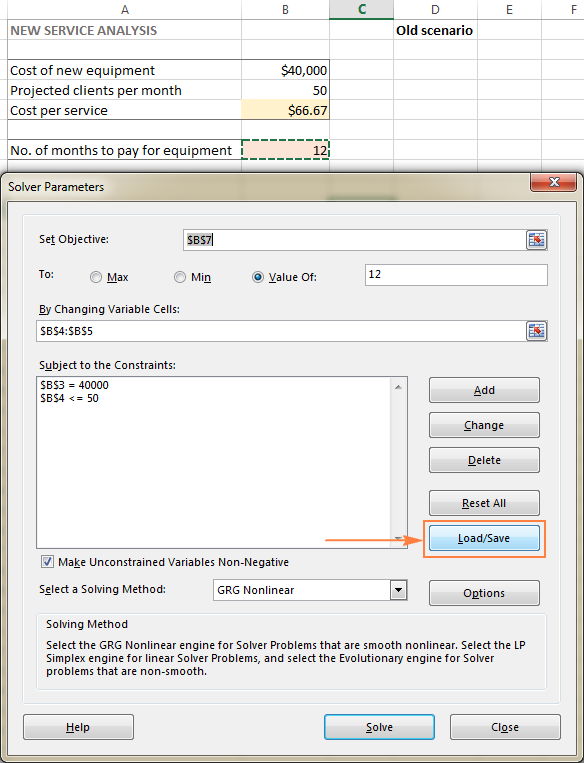
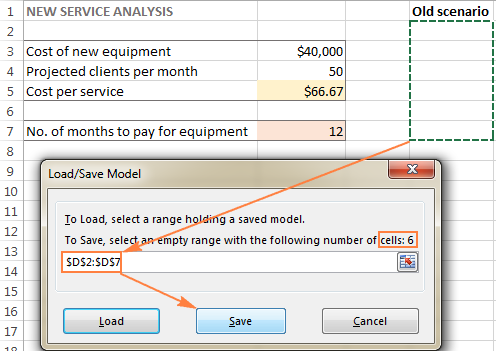
Ταυτόχρονα, η Παράμετροι επιλύτη θα εμφανιστεί το παράθυρο όπου μπορείτε να αλλάξετε τους περιορισμούς σας και να δοκιμάσετε διάφορες επιλογές "τι θα γινόταν αν".
Φόρτωση του αποθηκευμένου μοντέλου
Όταν αποφασίσετε να επαναφέρετε το αποθηκευμένο σενάριο, κάντε τα εξής:
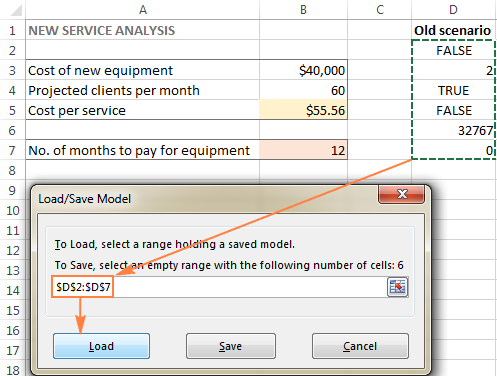
- Στο Παράμετροι επιλύτη παράθυρο, κάντε κλικ στο Φόρτωση/αποθήκευση κουμπί.
- Στο φύλλο εργασίας, επιλέξτε την περιοχή κελιών που περιέχει το αποθηκευμένο μοντέλο και κάντε κλικ στο κουμπί Φορτίο :
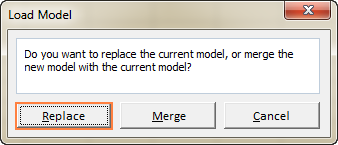
Αλγόριθμοι Excel Solver
Κατά τον ορισμό ενός προβλήματος για τον Επιλύτη Excel, μπορείτε να επιλέξετε μία από τις ακόλουθες μεθόδους στο πεδίο Επιλέξτε μια μέθοδο επίλυσης πτυσσόμενο πλαίσιο:
- GRG Nonlinear. Γενικευμένη μειωμένη κλίση Μη γραμμική αλγόριθμος χρησιμοποιείται για προβλήματα που είναι ομαλά μη γραμμικά, δηλαδή στα οποία τουλάχιστον ένας από τους περιορισμούς είναι μια ομαλή μη γραμμική συνάρτηση των μεταβλητών απόφασης. Περισσότερες λεπτομέρειες μπορείτε να βρείτε εδώ.
- LP Simplex Η μέθοδος επίλυσης LP Simplex βασίζεται στον αλγόριθμο Simplex που δημιούργησε ο Αμερικανός μαθηματικός επιστήμονας George Dantzig. Χρησιμοποιείται για την επίλυση των λεγόμενων Γραμμικός Προγραμματισμός προβλήματα - μαθηματικά μοντέλα των οποίων οι απαιτήσεις χαρακτηρίζονται από γραμμικές σχέσεις, δηλαδή αποτελούνται από έναν ενιαίο στόχο που αντιπροσωπεύεται από μια γραμμική εξίσωση που πρέπει να μεγιστοποιηθεί ή να ελαχιστοποιηθεί. Για περισσότερες πληροφορίες, ανατρέξτε σε αυτή τη σελίδα.
- Εξελικτική Χρησιμοποιείται για μη ομαλά προβλήματα, τα οποία είναι ο πιο δύσκολος τύπος προβλημάτων βελτιστοποίησης που επιλύονται, επειδή ορισμένες από τις συναρτήσεις είναι μη ομαλές ή ακόμη και ασυνεχείς, και επομένως είναι δύσκολο να προσδιοριστεί η κατεύθυνση προς την οποία μια συνάρτηση αυξάνεται ή μειώνεται. Για περισσότερες πληροφορίες, ανατρέξτε σε αυτή τη σελίδα.
Για να αλλάξετε τον τρόπο με τον οποίο ο Solver βρίσκει μια λύση, κάντε κλικ στο κουμπί Επιλογές στο κουμπί Παράμετροι επιλύτη και ρυθμίστε οποιαδήποτε ή όλες τις επιλογές στο παράθυρο διαλόγου GRG Μη γραμμική , Όλες οι μέθοδοι , και Εξελικτική καρτέλες.
Με αυτόν τον τρόπο μπορείτε να χρησιμοποιήσετε το Solver στο Excel για να βρείτε τις καλύτερες λύσεις για τα προβλήματα αποφάσεων που αντιμετωπίζετε. Και τώρα, ίσως θελήσετε να κατεβάσετε τα παραδείγματα του Excel Solver που συζητήθηκαν σε αυτό το σεμινάριο και να τα επεξεργαστείτε αντίστροφα για καλύτερη κατανόηση. Σας ευχαριστώ για την ανάγνωση και ελπίζω να σας δω στο ιστολόγιό μας την επόμενη εβδομάδα.

