Taula de continguts
El tutorial explica com afegir i on trobar Solver en diferents versions d'Excel, del 2016 al 2003. Els exemples pas a pas mostren com utilitzar el Solucionador d'Excel per trobar solucions òptimes per a la programació lineal i altres tipus de problemes.
Tothom sap que Microsoft Excel conté moltes funcions útils i eines potents que us poden estalviar hores de càlculs. Però, sabíeu que també té una eina que us pot ajudar a trobar solucions òptimes per als problemes de decisió?
En aquest tutorial, cobrirem tots els aspectes essencials del complement Excel Solver i oferirem un pas guia pas a pas sobre com utilitzar-lo de manera més eficaç.
Què és Excel Solver?
Excel Solver pertany a un conjunt especial de ordres sovint anomenades Eines d'anàlisi de si. Està dissenyat principalment per a la simulació i l'optimització de diversos models empresarials i d'enginyeria.
El complement de solucionador d'Excel és especialment útil per resoldre problemes de programació lineal, també coneguts com problemes d'optimització lineal i, per tant, de vegades s'anomena solucionador de programació lineal . A part d'això, pot gestionar problemes suaus no lineals i no suaus. Consulteu els algorismes d'Excel Solver per obtenir-ne més detalls.
Tot i que Solver no pot resoldre tots els problemes possibles, és molt útil a l'hora de tractar tot tipus de problemes d'optimització en què necessiteu prendre la millor decisió. Per exemple, es pots'ha de lliurar la quantitat demanada per cada client (B10:E10). Aquestes són cel·les Restringides .
El següent que heu de fer és calcular la quantitat total enviada des de cada magatzem (G7:G8) i la total de mercaderies rebudes per cada client (B9:E9). Podeu fer-ho amb fórmules Sum senzilles que es mostren a la captura de pantalla següent. A més, inseriu la fórmula SUMPRODUCT a C12 per calcular el cost total de l'enviament:
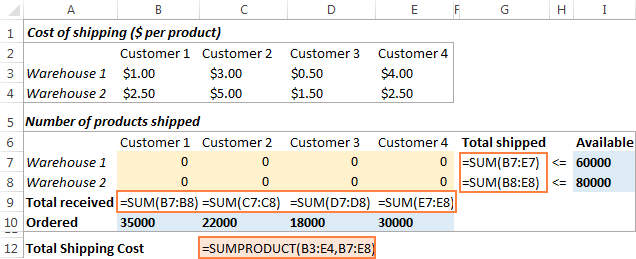
Per facilitar la comprensió del nostre model d'optimització del transport, creeu els intervals amb nom següents:
| Nom de la gamma | Cèl·lules | Paràmetre del solucionador |
| Productes_enviats | B7: E8 | Cel·les variables |
| Disponible | I7:I8 | Restricció |
| Total_enviat | G7:G8 | Restricció |
| Ordenat | B10:E10 | Restricció |
| Total_rebut | B9:E9 | Restricció |
| Cost_enviament | C12 | Objectiu |
L'últim que us queda per fer és configurar els paràmetres del solucionador d'Excel:
- Objectiu: cost_enviament establert a Min.
- Cel·les variables: Products_shipped
- Restriccions: Total_received = Ordered and Total_shipped <= Available
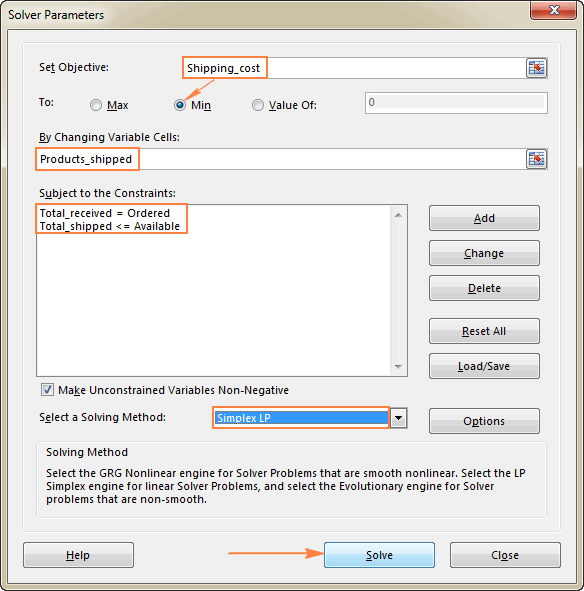
Si us plau, pagueu l'atenció que hem escollitel mètode de resolució Simplex LP en aquest exemple perquè estem tractant amb el problema de programació lineal. Si no esteu segur de quin tipus de problema és el vostre, podeu deixar el mètode de resolució per defecte GRG Nonlinear . Per obtenir més informació, vegeu algorismes de solucionador d'Excel.
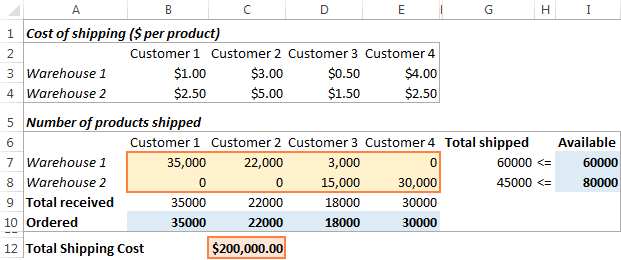
Solució
Feu clic al botó Resol a la part inferior de la finestra Paràmetres del solucionador i rebrà la teva resposta. En aquest exemple, el complement de solucionador d'Excel va calcular la quantitat òptima de mercaderies per lliurar a cada client des de cada magatzem amb el cost total mínim d'enviament:
Com estalviar i carregueu els escenaris de solucionador d'Excel
Quan resolgueu un model determinat, és possible que vulgueu desar els valors de la vostra cel·la Variable com a escenari que podeu veure o reutilitzar més tard.
Per exemple, quan calculeu el cost mínim del servei al primer exemple tractat en aquest tutorial, és possible que vulgueu provar diferents nombres de clients previstos per mes i veure com això afecta el cost del servei. Aleshores, és possible que vulgueu desar l'escenari més probable que ja hàgiu calculat i restaurar-lo en qualsevol moment.
Desar un escenari de solucionador d'Excel es redueix a seleccionar un rang de cel·les per deseu les dades a. Càrrega un model de solucionador només és qüestió de proporcionar a l'Excel el rang de cel·les on es desa el model. Els passos detallats segueixen a continuació.
Desar el fitxermodel
Per desar l'escenari del solucionador d'Excel, seguiu els passos següents:
- Obriu el full de treball amb el model calculat i executeu el solucionador d'Excel.
- A la Finestra Paràmetres del solucionador , feu clic al botó Carrega/Desa .
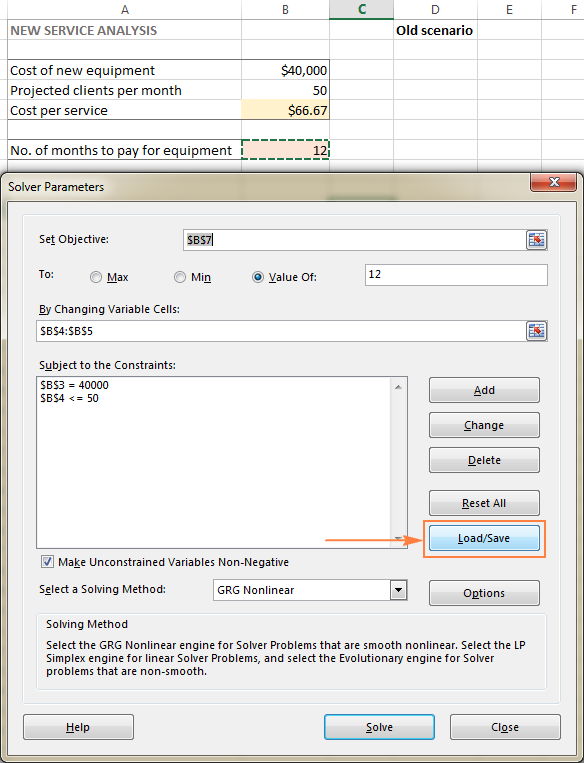
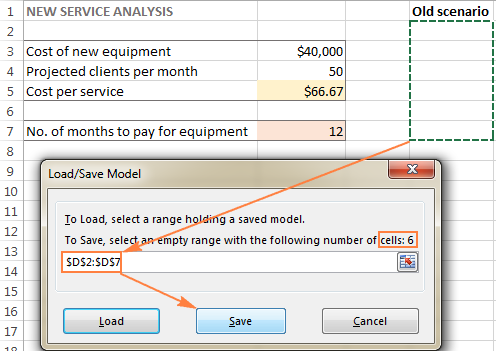
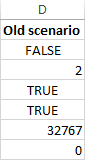
Al mateix temps, es mostrarà la finestra Paràmetres del solucionador on podeu canviar les vostres restriccions i provar diferents opcions "Què passa si".
Càrrega el model desat
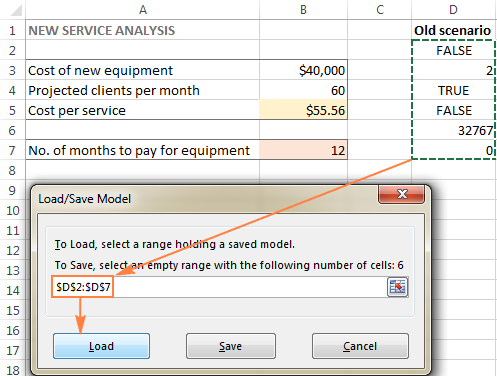
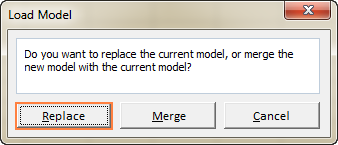
Quan decidiu restaurar l'escenari desat, feu el següent:
- A la finestra Paràmetres del solucionador , feu clic a Carrega/ Botó Desa .
- Al full de treball, seleccioneu l'interval de cel·les que contenen el model desat i feu clic a Carrega :
Algorismes del solucionador d'Excel
Quan definiu un problema per al solucionador d'Excel, podeu triar un dels mètodes següents al quadre desplegable Seleccioneu un mètode de resolució :
- GRG No lineal.L'algorisme Gradient reduït generalitzat no lineal s'utilitza per a problemes que són no lineals suaus, és a dir, en els quals almenys una de les restriccions és una funció no lineal suau de les variables de decisió. Podeu trobar més detalls aquí.
- LP Simplex . El mètode Simplex LP Solving es basa en l'algorisme Simplex creat per un científic matemàtic nord-americà George Dantzig. S'utilitza per resoldre els anomenats problemes de Programació lineal : models matemàtics els requisits dels quals es caracteritzen per relacions lineals, és a dir, consisteixen en un únic objectiu representat per una equació lineal que s'ha de maximitzar o minimitzar. Per obtenir més informació, consulteu aquesta pàgina.
- Evolucionari . S'utilitza per a problemes no suaus, que són el tipus de problemes d'optimització més difícils de resoldre perquè algunes de les funcions no són suaus o fins i tot discontinues i, per tant, és difícil determinar la direcció en què una funció està augmentant o disminuint. Per obtenir més informació, consulteu aquesta pàgina.
Per canviar com el solucionador troba una solució, feu clic al botó Opcions del quadre de diàleg Paràmetres del solucionador i configureu alguna o totes les opcions a les pestanyes GRG No lineal , Tots els mètodes i Evolucionari .
Així és com podeu utilitzar el solucionador a Excel per trobar les millors solucions als seus problemes de decisió. I ara, potser voldreudescarregueu els exemples de solucionador d'Excel que es discuteixen en aquest tutorial i feu-ne enginyeria inversa per entendre'ls millor. Us agraeixo la lectura i espero veure-us al nostre blog la setmana vinent.
ajudar-vos a maximitzar el retorn de la inversió, triar el pressupost òptim per a la vostra campanya publicitària, fer el millor horari de treball per als vostres empleats, minimitzar els costos de lliurament, etc.Com afegir Solver a Excel
El complement Solver s'inclou amb totes les versions de Microsoft Excel a partir del 2003, però no està habilitat de manera predeterminada.
Per afegir Solver al vostre Excel, seguiu els passos següents:
- A Excel 2010 - Excel 365, feu clic a Fitxer > Opcions .
A Excel 2007, feu clic al botó Microsoft Office i a continuació, feu clic a Opcions d'Excel .
- Al diàleg Opcions d'Excel , feu clic a Complements a la barra lateral esquerra, assegureu-vos que Complements d'Excel està seleccionat al quadre Gestiona a la part inferior de la finestra i feu clic a Vés .
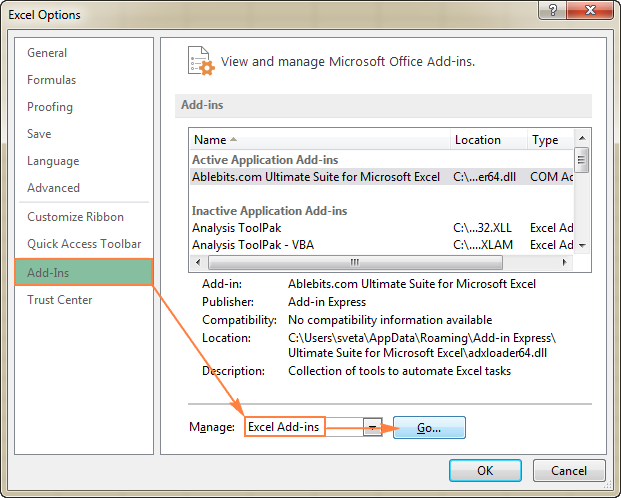
- A la casella Quadre de diàleg Complements , marqueu la casella Complement de solucionador i feu clic a D'acord :
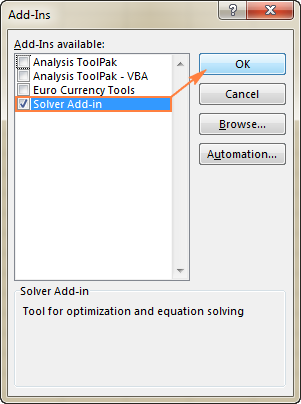
Per obtenir Solver a Excel 2003 , aneu al menú Eines i feu clic a Complements . A la llista Complements disponibles , marqueu la casella Complement de solucionador i feu clic a D'acord .
Nota. Si l'Excel mostra un missatge que indica que el complement del solucionador no està instal·lat actualment al vostre ordinador, feu clic a Sí per instal·lar-lo.
On és el solucionador a Excel?
A les versions modernes d'Excel, el botó Solucionador apareix a la pestanya Dades , a la Anàlisi grup:

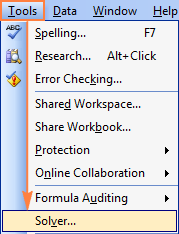
On ésSolver a Excel 2003?
Després de carregar el complement Solver a Excel 2003, la seva ordre s'afegeix al menú Eines :
Ara que ja sabeu on trobar Solver a Excel, obriu un full de treball nou i comencem!
Nota. Els exemples tractats en aquest tutorial fan servir Solver a Excel 2013. Si teniu una altra versió d'Excel, és possible que les captures de pantalla no coincideixin exactament amb la vostra versió, tot i que la funcionalitat del Solver és bàsicament la mateixa.
Com utilitzar el solucionador a Excel
Abans d'executar el complement del solucionador d'Excel, formuleu el model que voleu resoldre en un full de treball. En aquest exemple, anem a trobar una solució per al següent problema d'optimització senzill.
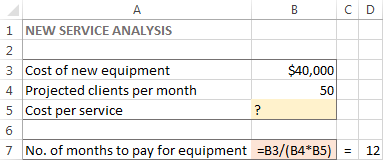
Problema . Suposant que sou el propietari d'un saló de bellesa i teniu previst oferir un nou servei als vostres clients. Per a això, heu de comprar un equip nou amb un cost de 40.000 dòlars, que s'ha de pagar a terminis en un termini de 12 mesos.
Objectiu : calcular el cost mínim per servei que us permetrà pagar. el nou equip dins del període de temps especificat.
Per a aquesta tasca, he creat el model següent:
I ara, vegem com Excel Solver pot trobar una solució a aquest problema.
1. Executeu l'Excel Solver
A la pestanya Dades , al grup Anàlisi , feu clic al botó Solucionador .
2. Definiu el problema
S'obrirà la finestra Paràmetres del solucionador on teniuper configurar els 3 components principals:
- Cel·la objectiu
- Cel·les variables
- Restriccions
Exactament què fa Excel Solver amb els paràmetres anteriors? Troba el valor òptim (màxim, mínim o especificat) per a la fórmula a la cel·la Objectiu canviant els valors de les cel·les Variable i subjecte a les limitacions de les Restriccions. cel·les.
Objectiu
La cel·la Objectiu (cel·la Objectiu en versions anteriors d'Excel) és la cel·la que conté una fórmula que representa l'objectiu, o objectiu, del problema. L'objectiu pot ser maximitzar, minimitzar o assolir algun valor objectiu.
En aquest exemple, la cel·la objectiu és B7, que calcula el termini de pagament mitjançant la fórmula =B3/(B4*B5) i el resultat de la fórmula hauria de ser igual a 12:
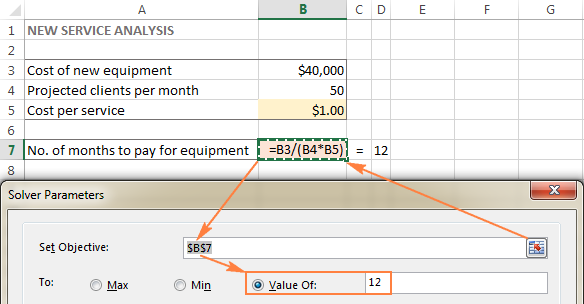
Cel·les variables
Cel·les variables ( Cel·les canviants o Ajustable cel·les en versions anteriors) són cel·les que contenen dades variables que es poden canviar per aconseguir l'objectiu. Excel Solver permet especificar fins a 200 cel·les variables.
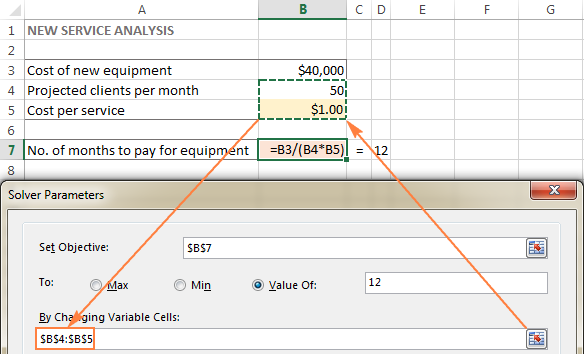
En aquest exemple, tenim un parell de cel·les els valors de les quals es poden canviar:
- Clients projectats per mes (B4) que haurien de ser inferior o igual a 50; i
- Cost per servei (B5) que volem que calculi Excel Solver.
Consell. Si les cel·les o intervals variables del vostre model són no adjacents ,seleccioneu la primera cel·la o rang i, a continuació, manteniu premuda la tecla Ctrl mentre seleccioneu altres cel·les i/o intervals. O bé, escriviu els intervals manualment, separats per comes.
Restriccions
El solucionador d'Excel Restriccions són restriccions o límits de les possibles solucions al problema. Per dir-ho d'una altra manera, les restriccions són les condicions que s'han de complir.
Per afegir una o més restriccions, feu el següent:
- Feu clic a Afegeix botó dret al quadre " Subjecte a les restriccions ".
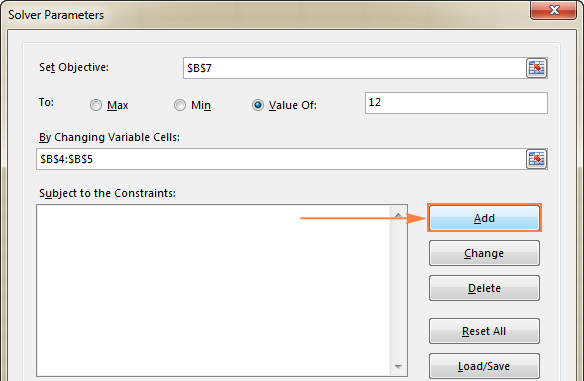
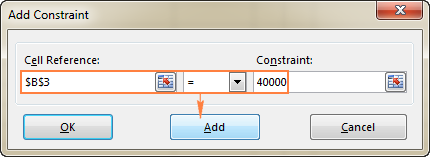
- A la finestra Restricció , introduïu una restricció.
- Feu clic al botó Afegeix per afegir la restricció a la llista.
- Continua introduint altres restriccions.
- Després d'haver introduït la restricció final, feu clic a D'acord per tornar a la finestra principal Solucionador Paràmetres .
Excel Solver permet especificar les relacions següents entre la cel·la de referència i la restricció.
- Inferior o igual a , igual a i superior o igual a . Per establir aquestes relacions, seleccioneu una cel·la al quadre Referència de cel·la , escollint un dels signes següents: <= , =, o > ;= i, a continuació, escriviu un número, una referència de cel·la/nom de cel·la o una fórmula al quadre Restricció (vegeu la captura de pantalla anterior).
- Enter . Si la cel·la a la qual es fa referència ha de ser un nombre enter, seleccioneu int ,i la paraula nter apareixerà al quadre Restricció .
- Valors diferents . Si cada cel·la de l'interval de referència ha de contenir un valor diferent, seleccioneu dif i la paraula AllDifferent apareixerà al quadre Restricció .
- Binari . Si voleu limitar una cel·la de referència a 0 o 1, seleccioneu bin i la paraula binary apareixerà al quadre Restricció .
Nota. Les relacions int , bin i dif només es poden utilitzar per a les restriccions a les cel·les variables.
Per editar o suprimir una restricció existent, feu el següent:
- Al quadre de diàleg Paràmetres del solucionador , feu clic al botó restricció.
- Per modificar la restricció seleccionada, feu clic a Canvia i feu els canvis que vulgueu.
- Per suprimir la restricció, feu clic al botó Suprimeix .
En aquest exemple, les restriccions són:
- B3=40000 - el cost del nou equip és de 40.000 $.
- B4<=50 - el nombre de pacients previstos per mes en menors de 50 anys.
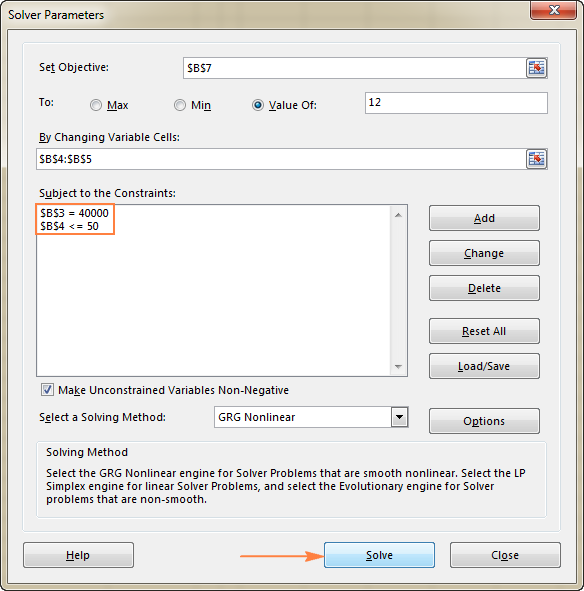
3. Resoldre el problema
Després d'haver configurat tots els paràmetres, feu clic al botó Resol a la part inferior de la finestra Paràmetres del solucionador (vegeu la captura de pantalla anterior) i deixeu que el complement de solucionador d'Excel troba la solució òptima per al vostre problema.
Depenent de la complexitat del model, la memòria de l'ordinador i la velocitat del processador, pot trigar uns quantssegons, uns quants minuts o fins i tot unes hores.
Quan Solver hagi acabat de processar, mostrarà la finestra de diàleg Resultats del solucionador , on seleccioneu Conserva la solució del solucionador i feu clic a D'acord :
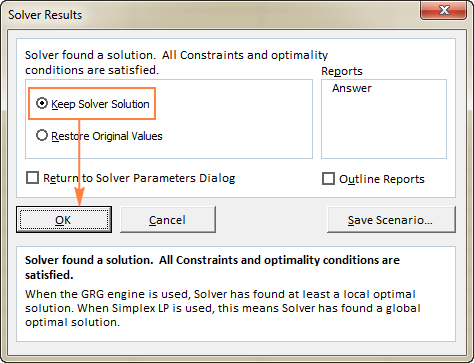
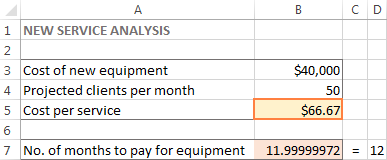
La finestra Resultat del solucionador es tancarà i apareixerà la solució al full de treball immediatament.
En aquest exemple, apareixen 66,67 $ a la cel·la B5, que és el cost mínim per servei que us permetrà pagar el nou equip en 12 mesos, sempre que hi hagi almenys 50 clients per cada mes:
Consells:
- Si el solucionador d'Excel ha estat processant un problema determinat durant massa temps, podeu interrompre el procés prement el botó Tecla Esc. Excel tornarà a calcular el full de treball amb els últims valors trobats per a les cel·les Variable .
- Per obtenir més detalls sobre el problema resolt, feu clic a un tipus d'informe al quadre Informes i, a continuació, feu clic a D'acord . L'informe es crearà en un full de treball nou:
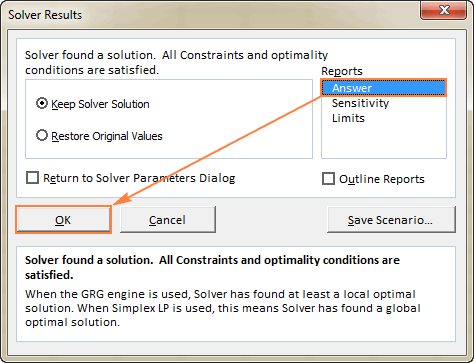
Ara que ja teniu la idea bàsica de com utilitzar el solucionador a Excel, mirem-ne més de prop un parell més exemples que us poden ajudar a entendre millor.
Excels de solucionador d'Excel
A continuació trobareu dos exemples més d'utilitzar l'additiu de solucionador d'Excel. Primer, trobarem una solució per a un trencaclosques conegut i després resoldrem un problema de programació lineal de la vida real.
Excel Solver exemple 1 (quadrat màgic)
ICreieu que tothom està familiaritzat amb els trencaclosques del "quadrat màgic" on heu de posar un conjunt de números en un quadrat perquè totes les files, columnes i diagonals sumin un nombre determinat.
Per exemple, coneixeu algun solució per al quadrat de 3x3 que conté nombres de l'1 al 9 on cada fila, columna i diagonal suma 15?
Probablement no sigui gran cosa resoldre aquest trencaclosques per assaig i error, però aposto que el solucionador trobarà la solució més ràpid. La nostra part de la feina és definir correctament el problema.
Per començar, introduïu els números de l'1 al 9 en una taula que consta de 3 files i 3 columnes. En realitat, el solucionador d'Excel no necessita aquests números, però ens ajudaran a visualitzar el problema. El que realment necessita el complement de solucionador d'Excel són les fórmules SUMA que sumen cada fila, columna i 2 diagonals:
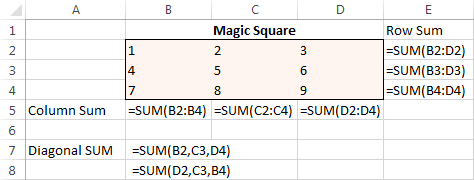
Amb totes les fórmules al seu lloc, executeu Solver i configureu-lo. els paràmetres següents:
- Estableix Objectiu . En aquest exemple, no necessitem establir cap objectiu, així que deixeu aquest quadre buit.
- Cel·les variables . Volem omplir nombres a les cel·les B2 a D4, així que seleccioneu l'interval B2:D4.
- Restriccions . S'han de complir les condicions següents:
- $B$2:$D$4 = Totes diferents: totes les cel·les variables haurien de contenir valors diferents.
- $B$2:$D$4 = enter - totes de les cel·les variables haurien de ser enters.
- $B$5:$D$5 = 15 - la suma dels valors de cadascunaLa columna ha de ser igual a 15.
- $E$2:$E$4 = 15 - la suma de valors de cada fila ha de ser igual a 15.
- $B$7:$B$8 = 15 - la suma de les dues diagonals hauria de ser igual a 15.
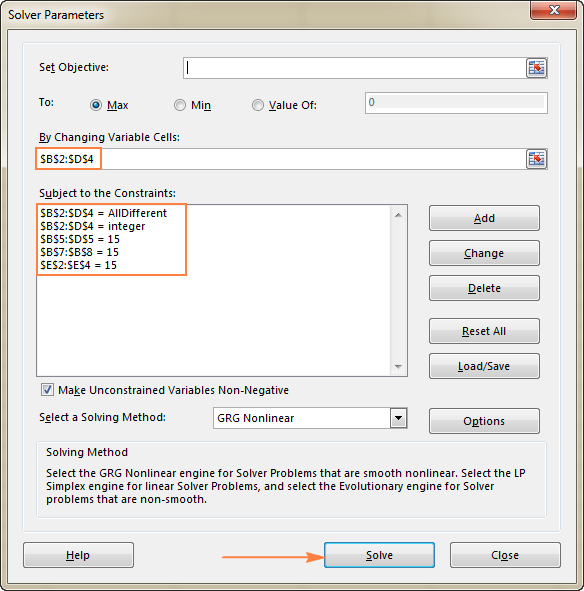
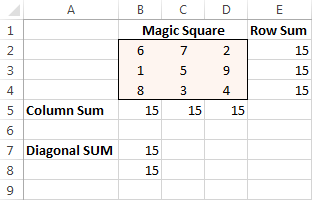
Finalment, feu clic al botó Resol i la solució hi és!
Excel Solver exemple 2 (problema de programació lineal)
Aquest és un exemple d'un problema d'optimització de transport senzill amb un objectiu lineal. Moltes empreses utilitzen models d'optimització més complexos d'aquest tipus per estalviar milers de dòlars cada any.
Problema : Voleu minimitzar el cost d'enviament de mercaderies de 2 magatzems diferents a 4 diferents. clients. Cada magatzem té una oferta limitada i cada client té una demanda determinada.
Objectiu : Minimitzar el cost total d'enviament, sense superar la quantitat disponible a cada magatzem i satisfer la demanda de cada client. .
Dades d'origen
Així és com es veu el nostre problema d'optimització del transport:
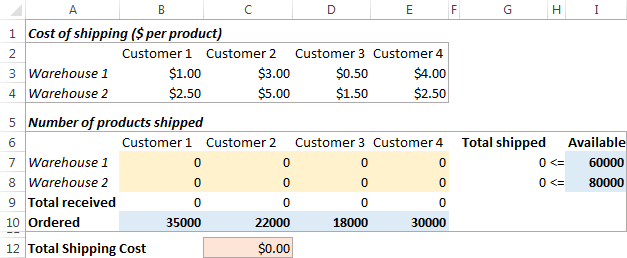
Formulant el model
Per definir el nostre problema de programació lineal per a l'Excel Solver, responem a les 3 preguntes principals:
- Quines decisions s'han de prendre? Volem calcular la quantitat òptima de mercaderies per lliurar a cada client des de cada magatzem. Aquestes són cel·les Variables (B7:E8).
- Quines són les restriccions? No es poden superar els subministraments disponibles a cada magatzem (I7:I8), i el

