Table of contents
该教程解释了如何在不同的Excel版本(从2016年到2003年)中添加和在哪里找到Solver。 逐步的例子显示了如何使用Excel Solver来寻找线性编程和其他类型问题的最优解。
每个人都知道,Microsoft Excel包含很多有用的函数和强大的工具,可以为你节省数小时的计算时间。 但你知道吗,它还有一个工具可以帮助你找到决策问题的最佳解决方案?
在本教程中,我们将介绍Excel Solver插件的所有基本方面,并逐步指导如何最有效地使用它。
什么是Excel解算器?
Excel解算器 属于一个特殊的命令集,通常被称为假设分析工具。 它的主要目的是模拟和优化各种商业和工程模型。
Excel Solver插件对解决线性编程问题(又称线性优化问题)特别有用,因此有时被称为 线性编程求解器 除此之外,它还可以处理平滑的非线性问题和非平滑问题。 更多细节请参见Excel解算器的算法。
虽然Solver不能破解所有可能的问题,但在处理各种需要做出最佳决策的优化问题时,它确实很有帮助。 例如,它可以帮助你实现投资回报的最大化,为你的广告活动选择最佳预算,为你的员工制定最佳工作计划,使交付成本最小化,等等。
如何在Excel中添加解算器
从2003年开始,所有版本的Microsoft Excel都包含了Solver插件,但它在默认情况下是不启用的。
要在你的Excel中添加Solver,请执行以下步骤。
- 在Excel 2010 - Excel 365中,点击 文件 > 选择 .
在Excel 2007中,点击 微软办公室 按钮,然后点击 Excel选项 .
- 在 Excel选项 对话框,点击 附加元件 在左边的侧栏,确保 Excel插件 中选择了 管理 窗口底部的方框,然后点击 进展 .
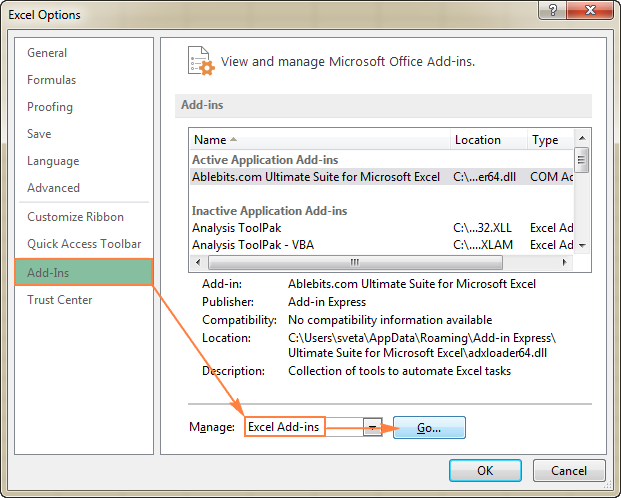
- 在 附加元件 对话框,选中 求解器插件 框,并点击 认可 :
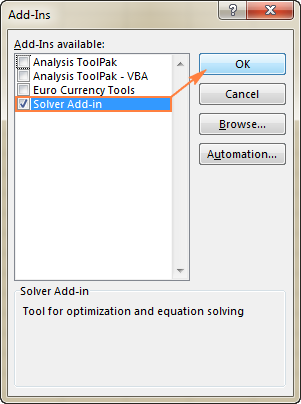
要想让Solver开启 Excel 2003 ,请到 工具 菜单,并点击 附加元件 在 附加元件 可用的 列表,检查 求解器插件 框,并点击 认可 .
注意:如果Excel显示一条消息说你的计算机上目前没有安装Solver插件,请点击 是 来安装它。
Excel中的Solver在哪里?
在现代版本的Excel中, 解决方法 按钮出现在 数据 选项卡,在 分析报告 组。

Excel 2003中的Solver在哪里?
解算器插件加载到Excel 2003后,其命令被添加到 工具 菜单。
现在你知道在哪里可以找到Excel中的Solver了,打开一个新的工作表,让我们开始吧!
注意:本教程中讨论的例子使用的是Excel 2013中的Solver,如果你有其他Excel版本,虽然Solver的功能基本相同,但屏幕截图可能与你的版本不完全一致。
如何在Excel中使用求解器
在运行Excel Solver插件之前,在工作表中制定你要解决的模型。 在这个例子中,让我们为以下简单的优化问题寻找解决方案。
问题 假设你是一家美容院的老板,你打算为你的客户提供一项新的服务。 为此,你需要购买一台新的设备,费用为40,000美元,应在12个月内分期支付。
目标 计算每项服务的最低成本,使你能在指定的时间范围内支付新设备的费用。
为了这项任务,我创建了以下模型。
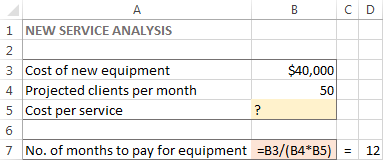
现在,让我们看看Excel Solver如何为这个问题找到解决方案。
1.运行Excel解算器
关于 数据 选项卡,在 分析报告 组,点击 解决方法 按钮。
2.定义问题
ǞǞǞ 解算器参数 窗口将打开,你必须在这里设置3个主要组件。
- 目标单元
- 可变的细胞
- 限制条件
究竟Excel Solver对上述参数做了什么? 它为公式中的内容找到了最佳值(最大、最小或指定)。 目标 中的值来改变单元格。 变化的 细胞,并受限制于 限制条件 细胞。
目标
ǞǞǞ 目标 细胞( 目标 在早期的Excel版本中是单元格 包含一个公式 该目标可以是最大化、最小化或实现某些目标值。
在这个例子中,目标单元格是B7,它使用公式计算出了付款期限 =B3/(B4*B5) 而公式的结果应该等于12。
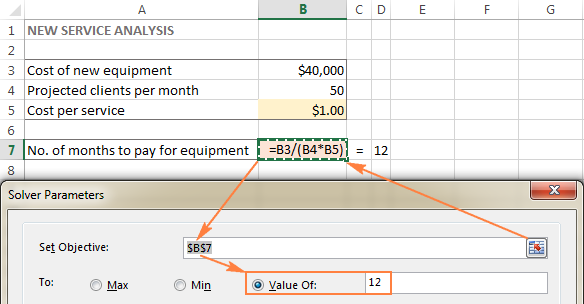
可变的细胞
变化的 细胞( 变化 细胞或 可调节的 Excel Solver允许指定多达200个变量单元格,在早期版本中是指包含可变数据的单元格。
在这个例子中,我们有几个单元格的值可以被改变。
- 每月预计客户数(B4)应小于或等于50;以及
- 我们希望Excel Solver计算的每项服务成本(B5)。
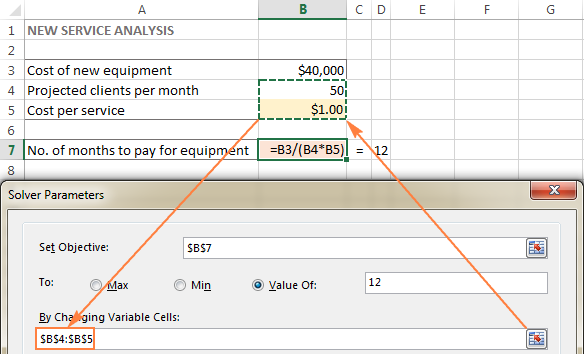
提示:如果你的模型中的变量单元格或范围是 不相邻的 选择第一个单元格或区域,然后按住Ctrl键,同时选择其他单元格和/或区域。 或者,手动输入范围,用逗号分隔。
限制条件
Excel解算器 限制条件 换句话说,约束是必须满足的条件。
要添加一个或多个约束条件,请执行以下操作。
- 点击 添加 按钮右侧的" 受制于限制条件 "的盒子。
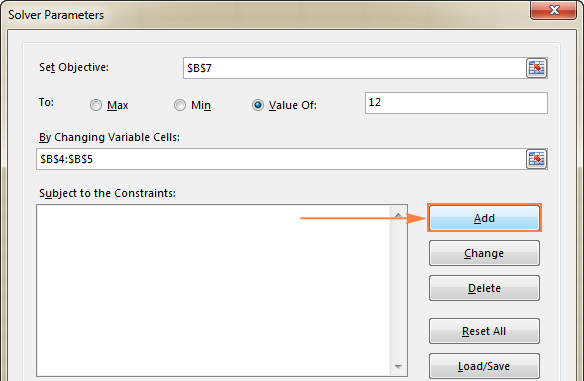
- 在 拘束 窗口,输入一个约束条件。
- 点击 添加 按钮将该制约因素添加到列表中。
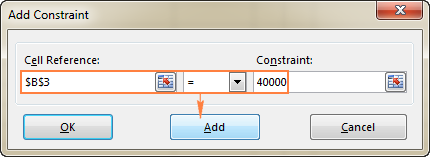
- 继续输入其他限制条件。
- 在你输入了最后的约束条件后,点击 认可 返回到主界面 解决方法 参数 窗口。
Excel解算器允许在引用的单元格和约束条件之间指定以下关系。
- 小于或等于 , 等于 ,以及 大于或等于 你通过选择一个单元格来设置这些关系。 细胞参考 框中,选择以下标志之一。 <= , =, 或 >= ,然后输入一个数字、单元格引用/单元格名称或公式。 拘束 框(请看上面的截图)。
- 整数 如果引用的单元格必须是一个整数,选择 䵮䵮 ,而这个词 整数 将出现在 拘束 箱子。
- 不同的价值 如果引用范围内的每个单元格都必须包含一个不同的值,选择 分歧 ,而这个词 差异化 将出现在 拘束 箱子。
- 二进制 如果你想把一个被引用的单元格限制为0或1,选择 斌 ,而这个词 二进制 将出现在 拘束 箱子。
注:该 䵮䵮 , 斌 ,以及 分歧 关系只能用于对变量单元的约束。
拟 编辑 或 删除 对一个现有的约束进行以下操作。
- 在 解算器参数 对话框,点击该约束。
- 要修改选定的约束,请点击 变化 并做你想做的改变。
- 要删除该约束,请点击 删除 按钮。
在这个例子中,约束条件是。
- B3=40000 - 新设备的成本是40000美元。
- B4<=50--每月预测的病人数量在50人以下。
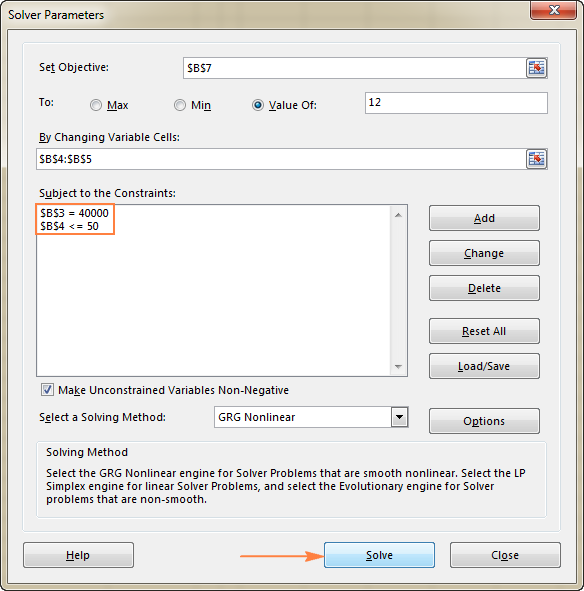
3. 解决问题
在你配置完所有参数后,点击 解决问题 的底部的按钮。 解算器参数 窗口(见上面的截图),让Excel Solver插件为你的问题找到最佳解决方案。
根据模型的复杂性、计算机内存和处理器速度,可能需要几秒钟、几分钟,甚至几小时。
当Solver完成处理后,它将显示 求解器结果 对话窗口,在这里你可以选择 保留解算器解决方案 并点击 认可 :
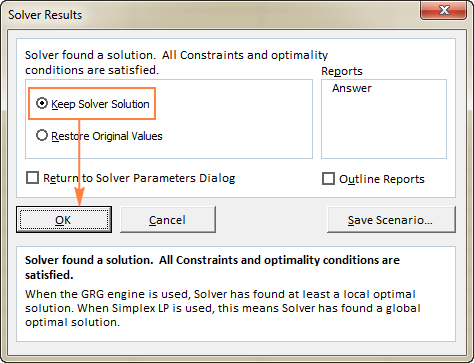
ǞǞǞ 解算结果 窗口将关闭,解决方案将立即出现在工作表中。
在这个例子中,B5单元格中出现了66.67美元,这是每个服务的最低成本,可以让你在12个月内支付新设备的费用,前提是每月至少有50个客户。
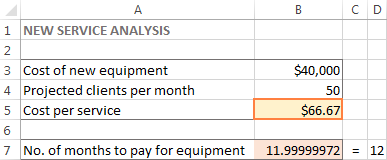
提示。
- 如果Excel解算器处理某个问题的时间过长,你可以按Esc键来中断这个过程。 Excel会用最后发现的数值重新计算工作表,为 变化的 细胞。
- 要获得有关已解决的问题的更多细节,请点击报告中的一个报告类型。 报告 框,然后点击 认可 该报告将在一个新的工作表中创建。
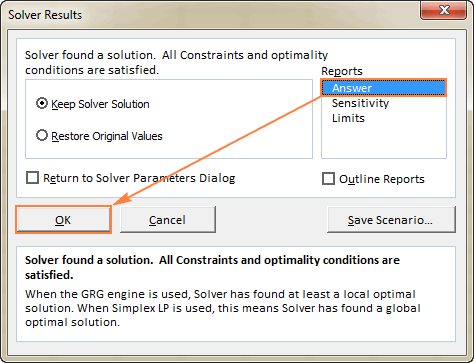
现在你已经对如何在Excel中使用Solver有了基本概念,让我们再仔细看看几个例子,也许能帮助你获得更多的理解。
Excel解算器实例
下面你将看到另外两个使用Excel Solver插件的例子。 首先,我们将找到一个著名谜题的解决方案,然后解决一个现实生活中的线性编程问题。
Excel求解器实例1(魔方)
我相信每个人都熟悉 "魔方 "谜题,你必须把一组数字放在一个正方形里,使所有的行、列和对角线相加都是某个数字。
例如,你知道一个包含1到9的数字的3x3正方形的解决方案,其中每一行、每一列和对角线加起来都是15吗?
通过试验和错误来解决这个难题可能没什么大不了的,但我敢打赌,解题器会更快地找到答案。 我们的部分工作是正确定义这个问题。
首先,在一个由3行3列组成的表格中输入从1到9的数字。 Excel求解器实际上不需要这些数字,但它们会帮助我们直观地了解问题。 Excel求解器插件真正需要的是将每一行、每一列和两个对角线相加的SUM公式。
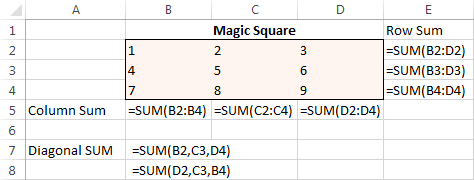
在所有公式就绪后,运行Solver并设置以下参数。
- 设置 目标 在这个例子中,我们不需要设置任何目标,所以让这个方框为空。
- 可变单元格 我们想在B2到D4单元格中填入数字,所以选择B2:D4单元格。
- 限制条件 应满足以下条件。
- $B$2:$D$4 = AllDifferent - 所有的变量单元格都应该包含不同的值。
- $B$2:$D$4=整数-所有的变量单元格都应该是整数。
- $B$5:$D$5=15--每一列的数值之和应该等于15。
- $E$2:$E$4 = 15 - 每一行的数值之和应该等于15。
- $B$7:$B$8=15--两条对角线之和应等于15。
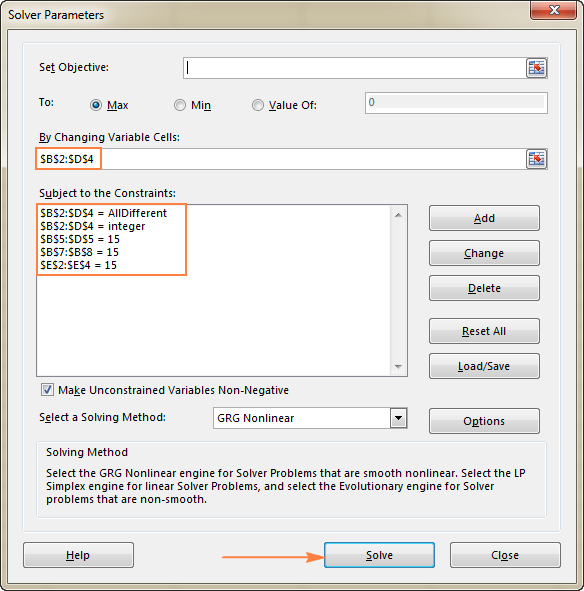
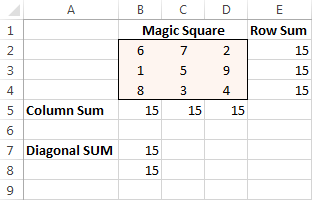
最后,点击 解决问题 按钮,而解决方案就在那里!
Excel求解器实例2(线性规划问题)。
这是一个具有线性目标的简单运输优化问题的例子。 这种更复杂的优化模型被许多公司用来每年节省成千上万美元。
问题 :你想将货物从2个不同的仓库运往4个不同的客户的成本降到最低。 每个仓库的供应量有限,每个客户都有一定的需求。
目标 :最大限度地降低总运输成本,不超过每个仓库的可用数量,并满足每个客户的需求。
来源数据
下面是我们的运输优化问题的样子。
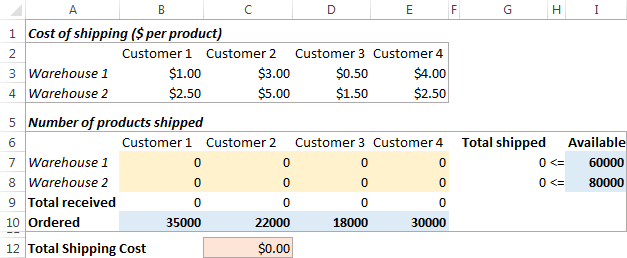
制订模型
为了定义我们的线性编程问题,让我们回答3个主要问题。
- 要做什么决定? 我们要计算出从每个仓库向每个客户交付的最佳货物数量。 这些是 变化的 细胞(B7:E8)。
- 什么是约束条件? 每个仓库的可用物资(I7:I8)不能超过,每个客户订购的数量(B10:E10)应该被交付。 这些是 受约束的 细胞 .
- 目标是什么? 最小的运输总成本。 而这就是我们的 目标 细胞(C12)。
接下来你要做的是计算每个仓库的总发货量(G7:G8)和每个客户的总收货量(B9:E9)。 你可以用下面截图中展示的简单的Sum公式来做。 另外,在C12中插入SUMPRODUCT公式来计算总的运输成本。
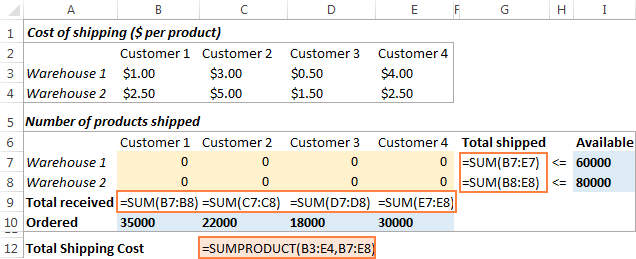
为了使我们的运输优化模型更容易理解,创建以下命名范围。
| 范围名称 | 细胞 | 解算器参数 |
| 产品_已发货 | B7:E8 | 可变的细胞 |
| 可用的 | I7:I8 | 拘束 |
| 发货总量 | G7:G8 | 拘束 |
| 已订购 | B10:E10 | 拘束 |
| 收到的总数 | B9:E9 | 拘束 |
| 运输费用 | C12 | 目标 |
留给你的最后一件事是配置Excel解算器参数。
- 目标:航运成本设置为 闵行区
- 变量单元:Products_shipped
- 约束条件:Total_received = Ordered and Total_shipped <= Available
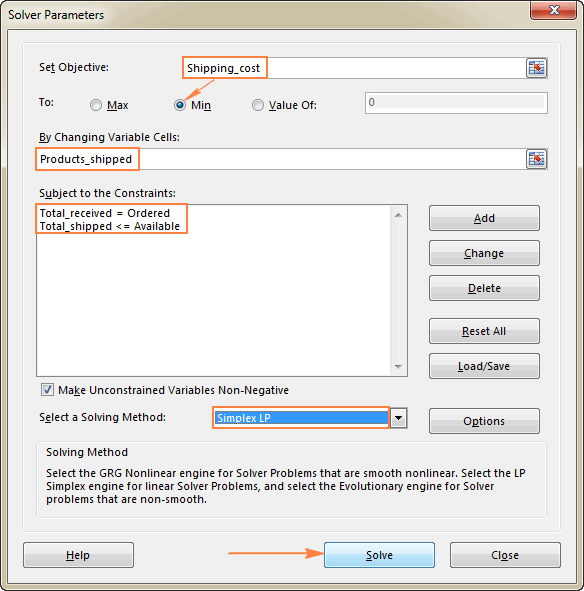
请注意,我们已经选择了 单纯的LP 如果你不确定你的问题是什么类型的,你可以在这个例子中保留默认的 GRG非线性 欲了解更多信息,请参见Excel解算器算法。
解决方案
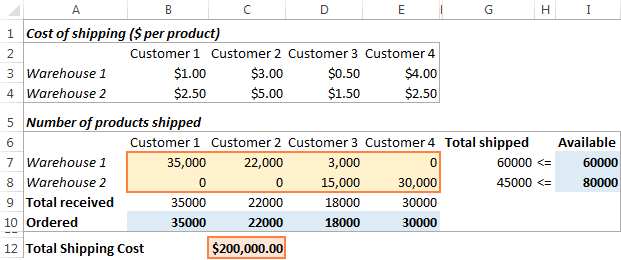
点击 解决问题 的底部的按钮。 解算器参数 在这个例子中,Excel求解器插件计算出了从每个仓库运送给每个客户的货物的最佳数量,并且运输的总成本最小。
如何保存和加载Excel求解器的情景
在解决某个模型时,你可能想保存你的 变化的 单元格的值作为一个场景,你可以在以后查看或重新使用。
例如,在本教程讨论的第一个例子中计算最低服务成本时,你可能想尝试每月不同的预计客户数量,看看这对服务成本有什么影响。 这时,你可能想保存你已经计算出的最可能的情况,并在任何时候恢复它。
节约 Excel解算器的方案可以归结为选择一个单元格区域来保存数据。 负载 下面是详细的步骤。
保存模型
要保存Excel求解器的方案,请执行以下步骤。
- 打开带有计算模型的工作表,运行Excel求解器。
- 在 解算器参数 窗口,点击 加载/保存 按钮。
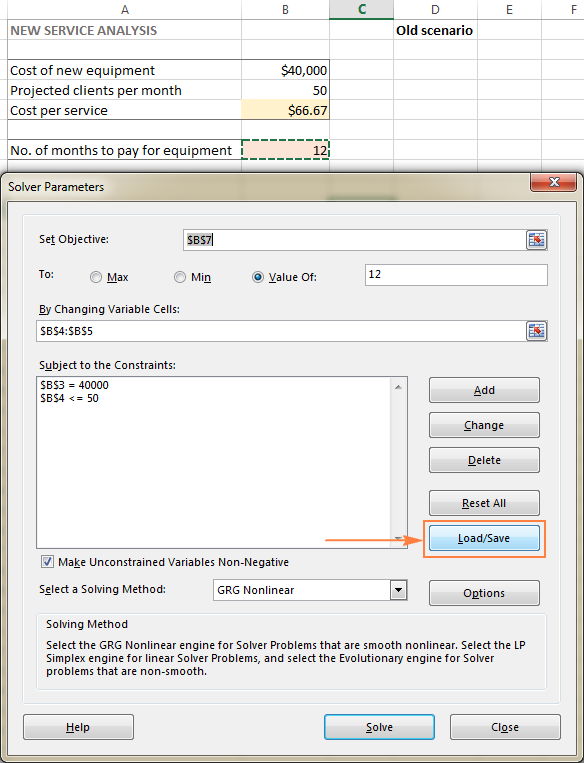
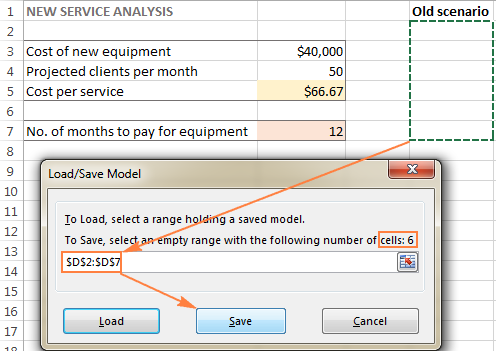
同时,在 解算器参数 窗口将出现,你可以改变你的约束条件,并尝试不同的 "假设 "选项。
加载已保存的模型
当你决定恢复已保存的情景时,请做以下工作。
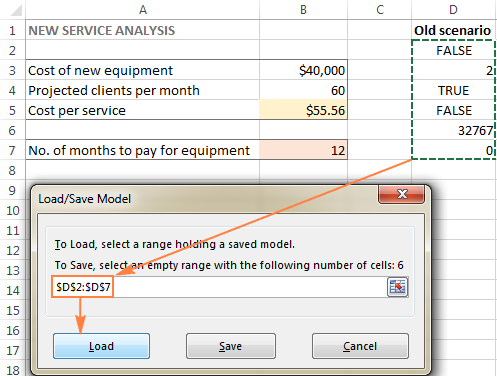
- 在 解算器参数 窗口,点击 加载/保存 按钮。
- 在工作表上,选择保存模型的单元格范围,然后点击 负载 :
Excel解算器的算法
当为Excel解题器定义一个问题时,你可以在以下方法中选择一种 选择一种解题方法 下拉框。
- GRG非线性。 广义的减梯度非线性 更多的细节可以在这里找到。
- LP单片机 Simplex LP求解方法是基于美国数学科学家George Dantzig创造的Simplex算法。 它被用来解决所谓的 线性编程 问题 - 数学模型,其要求的特点是线性关系,即包括一个由线性方程表示的单一目标,必须最大化或最小化。 更多信息,请查看此页面。
- 进化的 它用于非光滑问题,这是最难解决的一类优化问题,因为有些函数是非光滑的,甚至是不连续的,因此很难确定一个函数的增加或减少的方向。 更多信息,请见本页面。
要改变Solver寻找解决方案的方式,请点击 选择 中的按钮。 解算器参数 对话框,并配置任何或所有选项。 GRG非线性 , 所有方法 ,以及 进化的 标签。
这就是你如何使用Excel中的Solver来为你的决策问题找到最佳解决方案。 现在,你可能想下载本教程中讨论的Excel Solver实例,并对其进行逆向开发,以便更好地理解。 感谢你的阅读,希望下周在我们的博客上见到你。

