Sisukord
Õpik selgitab, kuidas lisada ja kust leida Solveri erinevates Exceli versioonides, alates 2016. aastast kuni 2003. Samm-sammult näidatakse, kuidas kasutada Exceli Solverit lineaarse programmeerimise ja muude probleemide optimaalsete lahenduste leidmiseks.
Kõik teavad, et Microsoft Excel sisaldab palju kasulikke funktsioone ja võimsaid tööriistu, mis võivad teid tundide kaupa arvutusi säästa. Kuid kas teadsite, et selles on ka tööriist, mis aitab teil leida optimaalseid lahendusi otsustusprobleemidele?
Selles õpetuses käsitleme kõiki Excel Solveri lisavõimaluse olulisi aspekte ja anname samm-sammult juhised selle kõige tõhusamaks kasutamiseks.
Mis on Excel Solver?
Exceli lahendaja kuulub spetsiaalsesse käskude kogumikku, mida sageli nimetatakse What-if Analysis Tools. See on mõeldud eelkõige erinevate äri- ja insenerimudelite simulatsiooniks ja optimeerimiseks.
Excel Solveri lisa on eriti kasulik lineaarse programmeerimise probleemide ehk lineaarsete optimeerimisprobleemide lahendamiseks ja seetõttu nimetatakse seda mõnikord ka lineaarse programmeerimise lahendaja Peale selle saab ta käsitleda siledat mittelineaarset ja mittesiledat probleemi. Täpsemalt vt Exceli lahendaja algoritme.
Kuigi Solver ei suuda lahendada kõiki võimalikke probleeme, on sellest tõesti abi igasuguste optimeerimisprobleemide lahendamisel, kus on vaja teha parim otsus. Näiteks aitab see teil maksimeerida investeeringute tasuvust, valida reklaamikampaania jaoks optimaalse eelarve, koostada töötajate jaoks parim tööplaan, minimeerida tarnekulusid jne.
Kuidas lisada Solver Excelisse
Solveri lisavõimalus on lisatud kõigile Microsoft Exceli versioonidele alates 2003. aastast, kuid see ei ole vaikimisi sisse lülitatud.
Solveri lisamiseks Exceli, tehke järgmised sammud:
- Excel 2010 - Excel 365, klõpsake Faili > Valikud .
Excel 2007-s klõpsake nuppu Microsoft Office nuppu ja seejärel klõpsake Exceli valikud .
- In the Exceli valikud dialoogis, klõpsake Add-Ins vasakul külgribal, veenduge, et Exceli lisandmoodulid on valitud Halda kasti akna allosas ja klõpsake nuppu Mine .
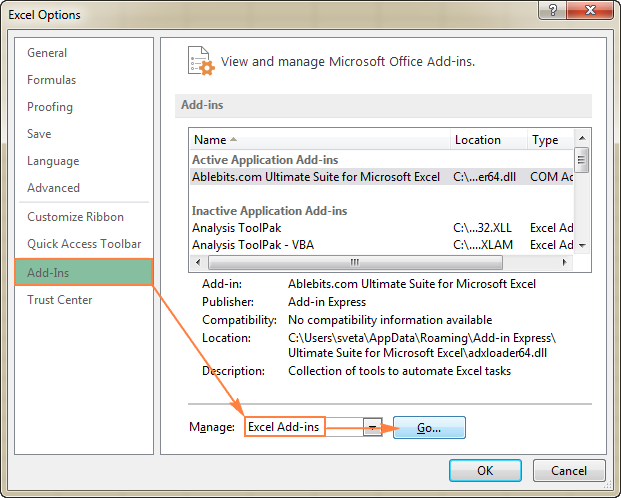
- In the Add-Ins dialoogiaknas, kontrollige Solver Add-in kasti ja klõpsake OK :
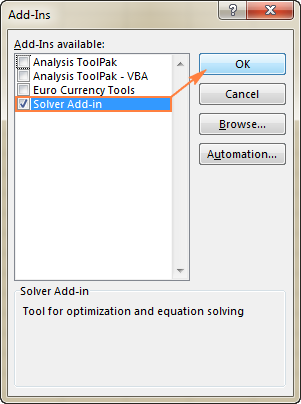
Solveri sisselülitamiseks Excel 2003 , minge aadressile Tööriistad menüü ja klõpsake Add-Ins . aastal Add-Ins saadaval nimekirja, kontrollige Solver Add-in kasti ja klõpsake OK .
Märkus. Kui Excel kuvab teate, et Solver Add-in ei ole praegu teie arvutisse installitud, klõpsake nuppu Jah selle paigaldamiseks.
Kus on Solver Excelis?
Exceli kaasaegsetes versioonides on Lahendaja nupp ilmub Andmed vahekaardil Analüüs rühm:

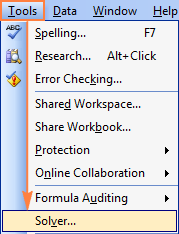
Kus on Solver Excel 2003-s?
Pärast seda, kui Solver Add-in on Excel 2003-i laaditud, lisatakse selle käsk käsureale Tööriistad menüü:
Nüüd, kui te teate, kust Solver Excelis leida, avage uus tööleht ja alustame!
Märkus. Selles õpetuses käsitletud näidetes kasutatakse Solverit Excel 2013-s. Kui teil on mõni teine Exceli versioon, ei pruugi ekraanipildid täpselt teie versioonile vastata, kuigi Solveri funktsioonid on põhimõtteliselt samad.
Kuidas kasutada Solverit Excelis
Enne Excel Solveri lisavõimaluse käivitamist sõnastage töölehel mudel, mida soovite lahendada. Selles näites otsime lahenduse järgmisele lihtsale optimeerimisprobleemile.
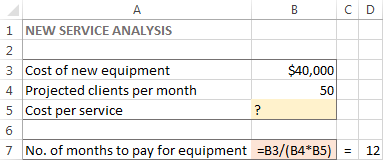
Probleem Oletame, et olete ilusalongi omanik ja kavatsete pakkuda oma klientidele uut teenust. Selleks peate ostma uue seadme, mis maksab 40 000 dollarit, mis tuleb tasuda 12 kuu jooksul osamaksetena.
Eesmärk : Arvutage minimaalne maksumus teenuse kohta, mis võimaldab teil uue seadme eest tasuda kindlaksmääratud aja jooksul.
Selle ülesande jaoks olen loonud järgmise mudeli:
Ja nüüd vaatame, kuidas Excel Solver leiab sellele probleemile lahenduse.
1. Käivitage Exceli lahendaja
On Andmed vahekaardil Analüüs rühma, klõpsake nuppu Lahendaja nupp.
2. Probleemi määratlemine
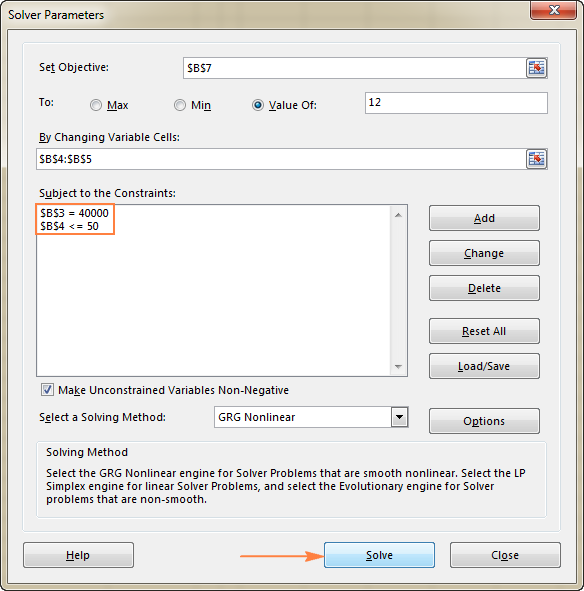
The Lahusti parameetrid avaneb aken, kus peate seadistama 3 põhikomponenti:
- Objektiivne lahter
- Muutlikud rakud
- Piirangud
Mida täpselt teeb Excel Solver ülaltoodud parameetritega? Ta leiab optimaalse väärtuse (maksimaalse, minimaalse või määratud) valemi jaoks valemiga Eesmärk lahtri väärtuste muutmisega Muutuv rakkude ja piirangutega, mis on sätestatud Piirangud rakud.
Eesmärk
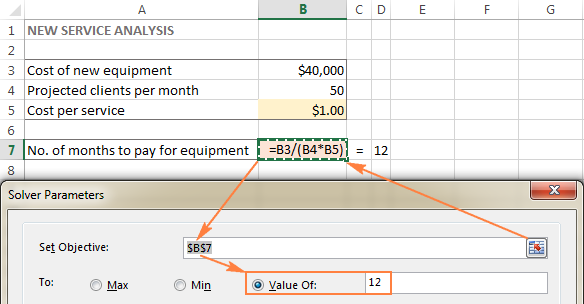
The Eesmärk rakk ( Eesmärk lahter varasemates Exceli versioonides) on lahter mis sisaldab valemit mis kujutab endast probleemi eesmärki või eesmärki. Eesmärk võib olla maksimeerimine, minimeerimine või mingi sihtväärtuse saavutamine.
Selles näites on objektiivne lahter B7, mis arvutab maksetähtaja valemiga =B3/(B4*B5) ja valemi tulemus peaks olema võrdne 12:
Muutlikud rakud
Muutuv rakud ( Muutuv rakud või Reguleeritav lahtrid varasemates versioonides) on lahtrid, mis sisaldavad muutuvaid andmeid, mida saab eesmärgi saavutamiseks muuta. Excel Solver võimaldab määrata kuni 200 muutuvat lahtrit.
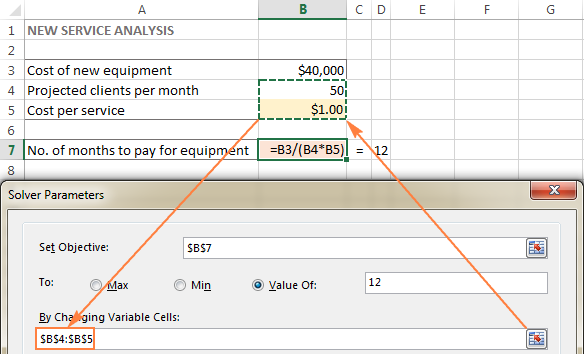
Selles näites on meil paar lahtrit, mille väärtusi saab muuta:
- Prognoositud kliendid kuus (B4), mis peaks olema väiksem või võrdne 50 kliendiga, ja
- Kulud teenuse kohta (B5), mida me tahame, et Excel Solver arvutaks.
Vihje. Kui teie mudeli muutuja lahtrid või vahemikud on mittekohalevad , valige esimene lahter või vahemik ja seejärel vajutage ja hoidke all Ctrl-klahvi, valides samal ajal teisi lahtreid ja/või vahemikke. Või sisestage vahemikud käsitsi, eraldades need komadega.
Piirangud
Exceli lahendaja Piirangud on probleemi võimalike lahenduste piirangud või piirid. Teisiti öeldes on piirangud tingimused, mis peavad olema täidetud.
Piirangu(te) lisamiseks tehke järgmist:
- Klõpsake nuppu Lisa nuppu paremale " Piirangute suhtes " kast.
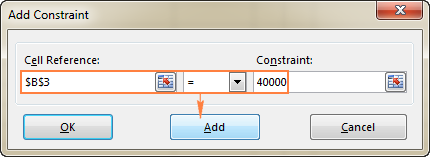
- In the Piirangud aknas, sisestage piirang.
- Klõpsake nuppu Lisa nuppu, et lisada piirangud loetellu.
- Jätkake muude piirangute sisestamist.
- Pärast lõpliku piirangu sisestamist klõpsake nuppu OK et pöörduda tagasi peamise Lahendaja Parameetrid aken.
Excel Solver võimaldab määrata järgmised seosed viidatud lahtri ja piirangu vahel.
- Vähem või võrdne , võrdne ja suurem või võrdne Need seosed määratakse, valides lahtri lahtrisse Raku viide kast, valides ühe järgmistest märkidest: <= , =, või >= ja seejärel sisestada number, lahtriviide / lahtri nimi või valem lahtrisse Piirangud kasti (vt ülaltoodud ekraanipilti).
- Tervearvuline Kui viidatud lahter peab olema täisarv, valige int ja sõna täisarv ilmub Piirangud kast.
- Erinevad väärtused Kui iga lahter viidatud vahemikus peab sisaldama erinevat väärtust, valige dif ja sõna AllDifferent ilmub Piirangud kast.
- Binaarne Kui soovite piirata viidatud lahtrit kas 0 või 1, valige bin ja sõna binaarne ilmub Piirangud kast.
Märkus. int , bin ja dif seoseid saab kasutada ainult muutuva lahtri piirangute puhul.
aadressile redigeeri või kustutada olemasolevat piirangut teha järgmist:
- In the Lahusti parameetrid dialoogiaknas, klõpsake piirangul.
- Valitud piirangu muutmiseks klõpsake Muuda ja tehke soovitud muudatused.
- Piirangu kustutamiseks klõpsake nuppu Kustuta nuppu.
Selles näites on piirangud järgmised:
- B3=40000 - uue seadme maksumus on 40 000 dollarit.
- B4<=50 - prognoositav patsientide arv kuus alla 50.
3. Lahendage probleem
Kui olete kõik parameetrid seadistanud, klõpsake nuppu Lahenda nuppu allosas Lahusti parameetrid aknas (vt ülaltoodud ekraanipilti) ja laske Excel Solver add-inil leida teie probleemile optimaalne lahendus.
Sõltuvalt mudeli keerukusest, arvuti mälust ja protsessori kiirusest võib see võtta aega mõned sekundid, mõned minutid või isegi mõned tunnid.
Kui Solver on töötlemise lõpetanud, kuvab ta ekraanile Lahendaja tulemused dialoogiaken, kus valite Hoidke lahendaja lahendus ja klõpsake OK :
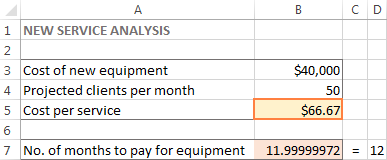
The Lahendaja Tulemus aken sulgub ja lahendus ilmub kohe töölehele.
Selles näites on lahtrisse B5 märgitud 66,67 dollarit, mis on minimaalne kulu teenuse kohta, mis võimaldab uue seadme eest tasuda 12 kuu jooksul, tingimusel, et kliente on vähemalt 50 kuus:
Näpunäited:
- Kui Exceli lahendaja on teatud probleemi liiga kaua töödelnud, saate protsessi katkestada, vajutades klahvi Esc. Excel arvutab töölehe uuesti, kasutades viimaseid leitud väärtusi, mida Muutuv rakud.
- Et saada rohkem üksikasju lahendatud probleemi kohta, klõpsake aruande tüübi kohta väljal Aruanded ja seejärel klõpsake nuppu OK Aruanne luuakse uuel töölehel:
Nüüd, kui teil on olemas põhiline ettekujutus sellest, kuidas kasutada Solverit Excelis, vaatame lähemalt veel paar näidet, mis võivad aidata teil paremini mõista.
Excel Solveri näited
Järgnevalt leiate veel kaks näidet Exceli Solveri lisavõimaluse kasutamise kohta. Kõigepealt leiame lahenduse tuntud mõistatusele ja seejärel lahendame reaalse lineaarse programmeerimise probleemi.
Exceli lahendaja näide 1 (maagiline ruut)
Usun, et kõik on tuttavad "maagilise ruudu" mõistatustega, kus tuleb panna arvude kogum ruutu nii, et kõik read, veerud ja diagonaalid annaksid kokku teatud arvu.
Kas te teate näiteks lahendust 3x3-ruutu jaoks, mis sisaldab numbreid 1-9, kus iga rida, veerg ja diagonaal annab kokku 15?
Tõenäoliselt ei ole selle mõistatuse lahendamine katse-eksituse teel suur probleem, kuid ma kihla vedan, et Solver leiab lahenduse kiiremini. Meie osa tööst on probleemi korralik defineerimine.
Alustuseks sisestage numbrid 1 kuni 9 tabelisse, mis koosneb 3 reast ja 3 veerust. Excel Solver ei vaja tegelikult neid numbreid, kuid need aitavad meil probleemi visualiseerida. Mida Excel Solveri add-in tegelikult vajab, on SUM valemid, mis summeerivad iga rea, veeru ja 2 diagonaali:
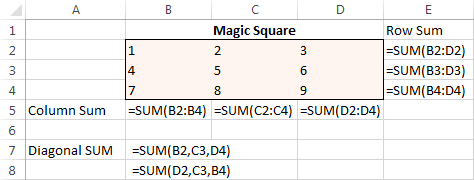
Kui kõik valemid on paigas, käivitage Solver ja seadistage järgmised parameetrid:
- Komplekt Eesmärk Selles näites ei ole meil vaja määrata ühtegi eesmärki, seega jätke see lahter tühjaks.
- Muutlikud rakud Me tahame täita lahtrite B2-D4 numbrid, seega valige vahemik B2:D4.
- Piirangud Järgmised tingimused peaksid olema täidetud:
- $B$2:$D$4 = AllDifferent - kõik muutuja lahtrid peaksid sisaldama erinevaid väärtusi.
- $B$2:$D$4 = täisarv - kõik muutuja lahtrid peaksid olema täisarvud.
- $B$5:$D$5 = 15 - iga veeru väärtuste summa peaks olema 15.
- $E$2:$E$4 = 15 - iga rea väärtuste summa peaks olema 15.
- $B$7:$B$8 = 15 - mõlema diagonaali summa peaks olema 15.
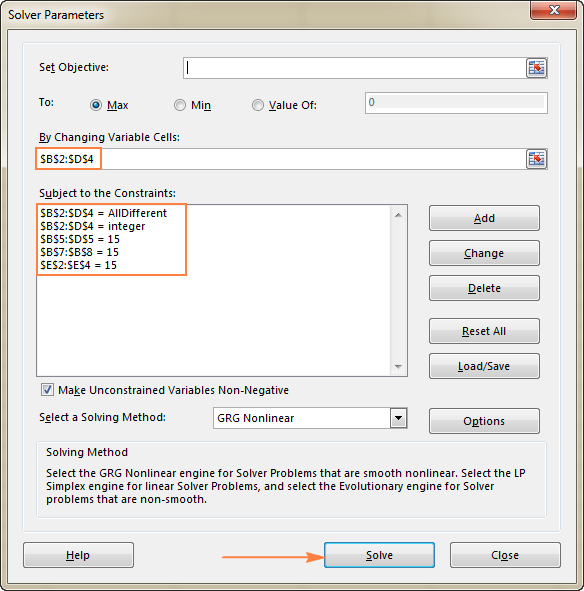
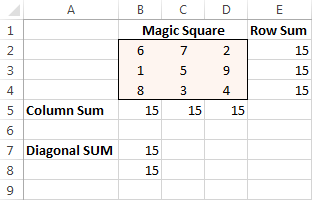
Lõpuks klõpsake nuppu Lahenda nuppu ja lahendus on olemas!
Exceli lahendaja näide 2 (lineaarse programmeerimise probleem)
See on näide lihtsast lineaarse eesmärgiga transpordi optimeerimisprobleemist. Selliseid keerulisemaid optimeerimismudeleid kasutavad paljud ettevõtted, et säästa igal aastal tuhandeid dollareid.
Probleem : Te soovite minimeerida kauba saatmise kulusid 2 erinevast laost 4-le erinevale kliendile. Igas laos on piiratud pakkumine ja igal kliendil on teatud nõudlus.
Eesmärk : Minimeerida kogutranspordikulud, mitte ületada igas laos saadaolevat kogust ja rahuldada iga kliendi nõudlust.
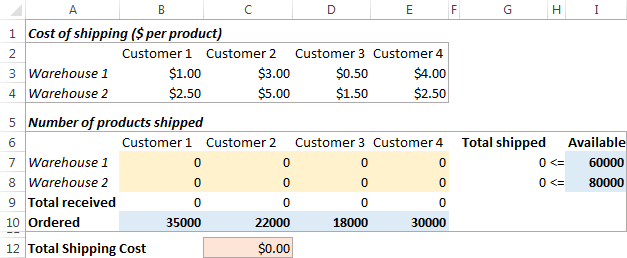
Allikasandmed
Meie transpordi optimeerimise probleem näeb välja järgmiselt:
Mudeli sõnastamine
Et määratleda meie lineaarse programmeerimise probleem Exceli lahendaja jaoks, vastame 3 põhiküsimusele:
- Milliseid otsuseid tuleb teha? Tahame arvutada optimaalse kaubakoguse, mida igale kliendile igast laost tarnida. Need on järgmised Muutuv rakud (B7:E8).
- Millised on piirangud? Igas laos olemasolevaid varusid (I7:I8) ei tohi ületada ja iga kliendi poolt tellitud kogus (B10:E10) peab olema tarnitud. Need on järgmised Piiratud rakud .
- Mis on eesmärk? Minimaalne kogukulu laevanduse. Ja see on meie Eesmärk rakk (C12).
Järgmisena peate arvutama igast laost lähetatud koguse (G7:G8) ja iga kliendi poolt vastuvõetud kauba koguhulga (B9:E9). Seda saate teha lihtsate Summa valemitega, mida on näidatud allpool oleval ekraanipildil. Samuti sisestage C12-sse valem SUMPRODUCT, et arvutada saatmise kogukulu:
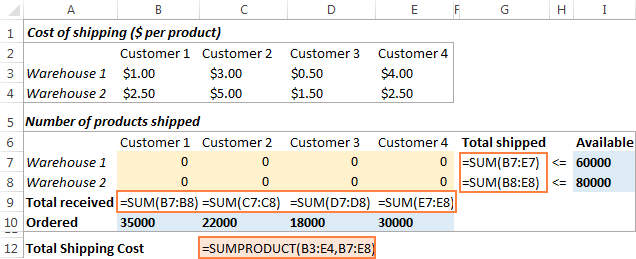
Et meie transpordi optimeerimise mudel oleks lihtsamini arusaadav, loome järgmised nimelised vahemikud:
| Vahemiku nimi | Rakud | Lahusti parameeter |
| Tooted_saadetud | B7:E8 | Muutlikud rakud |
| Saadaval | I7:I8 | Piirangud |
| Kokku_saadetud | G7:G8 | Piirangud |
| Tellitud | B10:E10 | Piirangud |
| Kokku_saadud | B9:E9 | Piirangud |
| Laevanduse_kulud | C12 | Eesmärk |
Viimane asi, mis teil veel teha tuleb, on Exceli lahendaja parameetrite konfigureerimine:
- Eesmärk: Shipping_cost seatud Min
- Muutujad: Products_shipped
- Piirangud: Total_received = tellitud ja Total_shipped <= saadaval.
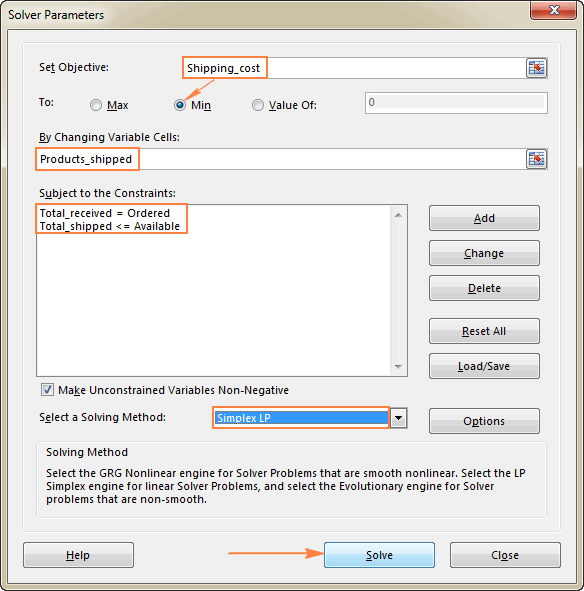
Palun pöörake tähelepanu, et me oleme valinud Simplex LP lahendamise meetodit selles näites, sest me tegeleme lineaarse programmeerimise probleemiga. Kui te ei ole kindel, millise probleemiga teie puhul on tegemist, võite jätta vaikimisi seadistuse GRG mittelineaarsed lahendamise meetod. Lisateavet leiate Excel Solveri algoritmidest.
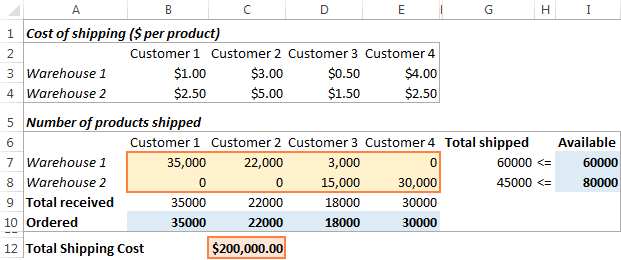
Lahendus
Klõpsake nuppu Lahenda nuppu allosas Lahusti parameetrid aknas ja saate vastuse. Selles näites arvutas Excel Solveri lisavahend välja optimaalse kaubakoguse, mida igale kliendile igast laost tarnida minimaalsete kogukuludega:
Kuidas salvestada ja laadida Excel Solveri stsenaariume
Teatud mudeli lahendamisel võite salvestada oma Muutuv lahtri väärtused stsenaariumina, mida saate hiljem vaadata või uuesti kasutada.
Näiteks, kui arvutate minimaalse teenusekulu kõige esimeses selles õpetuses käsitletud näites, võite proovida erinevaid prognoositavate klientide arvu kuus ja vaadata, kuidas see mõjutab teenusekulu. Seejuures võite salvestada juba arvutatud kõige tõenäolisemat stsenaariumi ja taastada selle igal hetkel.
Säästmine Excel Solveri stsenaarium taandub andmete salvestamiseks vajaliku rakkude vahemiku valimisele. Laadimine Solveri mudelit on lihtsalt vaja anda Excelile lahtrite vahemik, kuhu teie mudel on salvestatud. Järgnevalt järgnevad üksikasjalikud sammud.
Mudeli salvestamine
Exceli lahendaja stsenaariumi salvestamiseks tehke järgmised toimingud:
- Avage tööleht arvutatud mudeliga ja käivitage Exceli lahendaja.
- In the Lahusti parameetrid aknas, klõpsake nuppu Laadimine/Salvestamine nupp.
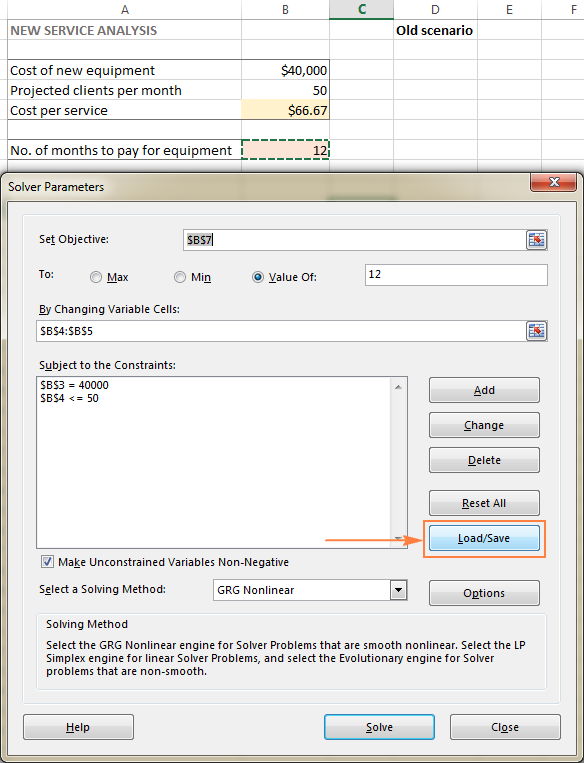
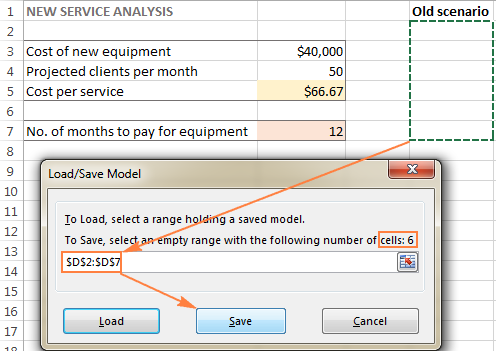
Samal ajal on Lahusti parameetrid ilmub aken, kus saate muuta piiranguid ja proovida erinevaid "mis oleks, kui" valikuid.
Salvestatud mudeli laadimine
Kui otsustate salvestatud stsenaariumi taastada, tehke järgmist:
- In the Lahusti parameetrid aknas, klõpsake nuppu Laadimine/Salvestamine nupp.
- Valige töölehel salvestatud mudelit sisaldavate lahtrite vahemik ja klõpsake nuppu Koormus :
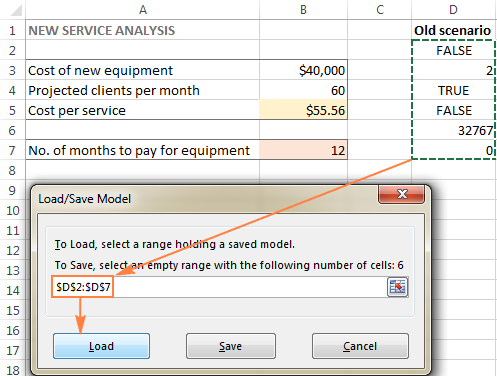
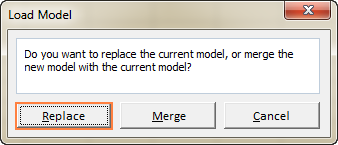
Exceli lahendaja algoritmid
Exceli lahendaja jaoks probleemi määratlemisel saate valida ühe järgmistest meetoditest, mis on esitatud jaotises Valige lahendamismeetod rippmenüü:
- GRG Nonlinear. Üldistatud vähendatud gradienti mittelineaarsed algoritmi kasutatakse probleemide puhul, mis on siledad mittelineaarsed, st kus vähemalt üks kitsendustest on sujuv mittelineaarne funktsioon otsustusmuutujast. Täpsemalt saab lugeda siit.
- LP Simplex Simplex LP lahendamise meetod põhineb Simplex algoritmil, mille on loonud Ameerika matemaatikauurija George Dantzig. Seda kasutatakse nn. Lineaarne programmeerimine probleemid - matemaatilised mudelid, mille nõudeid iseloomustavad lineaarsed seosed, st koosnevad ühest eesmärgist, mida esindab lineaarne võrrand, mida tuleb maksimeerida või minimeerida. Lisateavet leiate sellelt leheküljelt.
- Evolutsiooniline Seda kasutatakse mittesiledate probleemide puhul, mis on kõige raskemini lahendatavad optimeerimisprobleemid, sest mõned funktsioonid on mittesiledad või isegi ebastabiilsed ja seetõttu on raske määrata, millises suunas funktsioon kasvab või kahaneb. Lisateavet leiate sellelt leheküljelt.
Selleks, et muuta lahenduse leidmise viisi, klõpsake nuppu Valikud nuppu Lahusti parameetrid dialoogiaknas ja konfigureerige ükskõik milliseid või kõiki valikuid. GRG mittelineaarsed , Kõik meetodid ja Evolutsiooniline vahekaardid.
Nii saate kasutada Solverit Excelis, et leida parimad lahendused oma otsustusprobleemidele. Ja nüüd võite alla laadida selles õpetuses käsitletud Exceli Solveri näited ja neid parema arusaamise eesmärgil ümber pöörata. Tänan teid lugemise eest ja loodan, et näeme teid järgmisel nädalal meie blogis.

