Բովանդակություն
Ուսուցումը բացատրում է, թե ինչպես ավելացնել և որտեղ գտնել Solver Excel-ի տարբեր տարբերակներում, 2016-ից մինչև 2003 թվականները: Քայլ առ քայլ օրինակները ցույց են տալիս, թե ինչպես օգտագործել Excel Solver-ը գծային ծրագրավորման և այլ տեսակի օպտիմալ լուծումներ գտնելու համար: խնդիրներ:
Բոլորը գիտեն, որ Microsoft Excel-ը պարունակում է բազմաթիվ օգտակար գործառույթներ և հզոր գործիքներ, որոնք կարող են խնայել ժամեր հաշվարկներ կատարելը: Բայց դուք գիտե՞ք, որ այն նաև ունի գործիք, որը կարող է օգնել ձեզ գտնել որոշումների խնդիրների օպտիմալ լուծումներ:
Այս ձեռնարկում մենք պատրաստվում ենք լուսաբանել Excel Solver հավելյալի բոլոր էական կողմերը և տրամադրել մի քայլ: -Քայլ առ քայլ ուղեցույց, թե ինչպես օգտագործել այն առավել արդյունավետ:
Ի՞նչ է Excel Solver-ը:
Excel Solver պատկանում է հատուկ փաթեթի հրամաններ, որոնք հաճախ կոչվում են What-if Analysis Tools: Այն հիմնականում նպատակաուղղված է տարբեր բիզնեսի և ինժեներական մոդելների մոդելավորման և օպտիմալացման համար:
Excel Solver հավելումը հատկապես օգտակար է գծային ծրագրավորման խնդիրներ լուծելու համար, այսինքն՝ գծային օպտիմալացման խնդիրներ, և, հետևաբար, երբեմն կոչվում է գծային ծրագրավորման լուծիչ : Բացի դրանից, այն կարող է հարթել ոչ գծային և ոչ հարթ խնդիրներ: Լրացուցիչ մանրամասների համար տե՛ս Excel Solver ալգորիթմները:
Չնայած Solver-ը չի կարող կոտրել բոլոր հնարավոր խնդիրը, այն իսկապես օգտակար է, երբ գործ ունենք օպտիմալացման բոլոր տեսակի խնդիրների հետ, որտեղ դուք պետք է լավագույն որոշում կայացնեք: Օրինակ, դա կարող էՅուրաքանչյուր հաճախորդի կողմից պատվիրված քանակությունը (B10:E10) պետք է առաքվի: Սրանք Սահմանափակված բջիջներ են:
Հաջորդ բանը, որ պետք է անեք, յուրաքանչյուր պահեստից առաքված ընդհանուր քանակի հաշվարկն է (G7:G8) և յուրաքանչյուր հաճախորդի կողմից ստացված ընդհանուր ապրանքները (B9:E9): Դուք կարող եք դա անել ստորև ներկայացված սքրինշոթում ցուցադրված պարզ գումարի բանաձևերով: Նաև մտցրեք SUMPRODUCT բանաձևը C12-ում՝ առաքման ընդհանուր արժեքը հաշվարկելու համար.
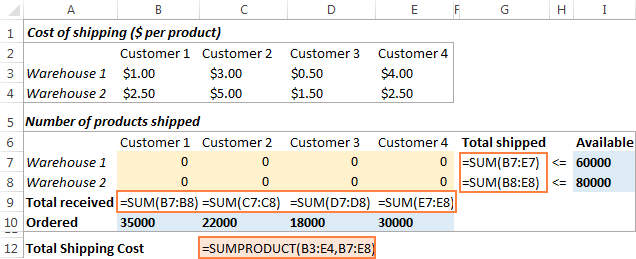
Տրանսպորտի օպտիմալացման մեր մոդելն ավելի հեշտ հասկանալի դարձնելու համար ստեղծեք հետևյալ անվանվող միջակայքերը.
| Տեսակի անվանումը | Cells | Solver պարամետր |
| Products_shipped | B7: E8 | Փոփոխական բջիջներ |
| Հասանելի է | I7:I8 | Սահմանափակում |
| Ընդհանուր_առաքված | G7:G8 | Սահմանափակում |
| Պատվիրված է | B10:E10 | Սահմանափակում |
| Ընդհանուր_ստացված | B9:E9 | Սահմանափակում | Առաքման_արժեք | C12 | Օբյեկտիվ |
Վերջին բանը, որ ձեզ մնում է անել, Excel Solver-ի պարամետրերի կարգավորումն է.
- Նպատակը. Առաքման_արժեքը սահմանվել է Min.
- Փոփոխական բջիջներ. Products_shipped
- Սահմանափակումներ. Total_received = Պատվիրված և Total_shipped <= Հասանելի է
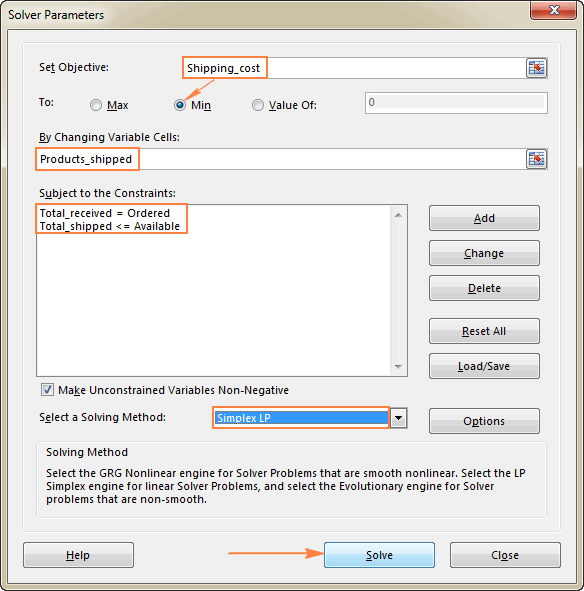
Խնդրում ենք վճարել ուշադրություն, որը մենք ընտրել ենքայս օրինակում Simplex LP լուծելու մեթոդը, քանի որ մենք գործ ունենք գծային ծրագրավորման խնդրի հետ: Եթե վստահ չեք, թե ինչ տեսակի խնդիր է ձերը, կարող եք թողնել լռելյայն GRG Ոչ գծային լուծման մեթոդը: Լրացուցիչ տեղեկությունների համար տե՛ս Excel Solver ալգորիթմները:
Լուծում
Սեղմեք Լուծել կոճակը Solver Parameters պատուհանի ներքևում, և դուք կստանաք ձեր պատասխանը: Այս օրինակում Excel Solver հավելումը հաշվարկել է ապրանքների օպտիմալ քանակությունը յուրաքանչյուր հաճախորդին առաքելու համար յուրաքանչյուր պահեստից՝ առաքման նվազագույն ընդհանուր արժեքով.
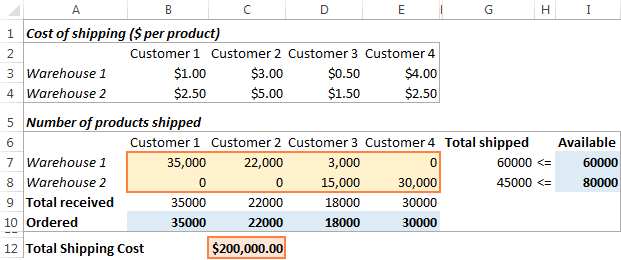
Ինչպես խնայել և բեռնեք Excel Solver-ի սցենարները
Որոշ մոդել լուծելիս կարող եք պահպանել ձեր Փոփոխական բջիջների արժեքները որպես սցենար, որը կարող եք դիտել կամ նորից օգտագործել ավելի ուշ:
Օրինակ, այս ձեռնարկում քննարկված առաջին օրինակում ծառայության նվազագույն արժեքը հաշվարկելիս կարող եք փորձել տարբեր թվով կանխատեսվող հաճախորդներ ամսական և տեսնել, թե դա ինչպես է ազդում ծառայության արժեքի վրա: Ընդ որում, դուք կարող եք պահպանել ամենահավանական սցենարը, որն արդեն հաշվարկել եք և ցանկացած պահի վերականգնել այն:
Պահպանել Excel Solver-ի սցենարը հանգում է նրան, որ ընտրեք մի շարք բջիջներ: պահպանել տվյալները: Բեռնում Լուծվող մոդելը պարզապես Excel-ին տրամադրելու խնդիր է այն բջիջների շրջանակը, որտեղ պահվում է ձեր մոդելը: Մանրամասն քայլերը հետևում են ստորև:
Պահպանում էմոդել
Excel Solver-ի սցենարը պահպանելու համար կատարեք հետևյալ քայլերը.
- Բացեք աշխատաթերթը հաշվարկված մոդելով և գործարկեք Excel Solver-ը:
- Մտքում Solver Parameters պատուհանը, սեղմեք Load/Save կոճակը:
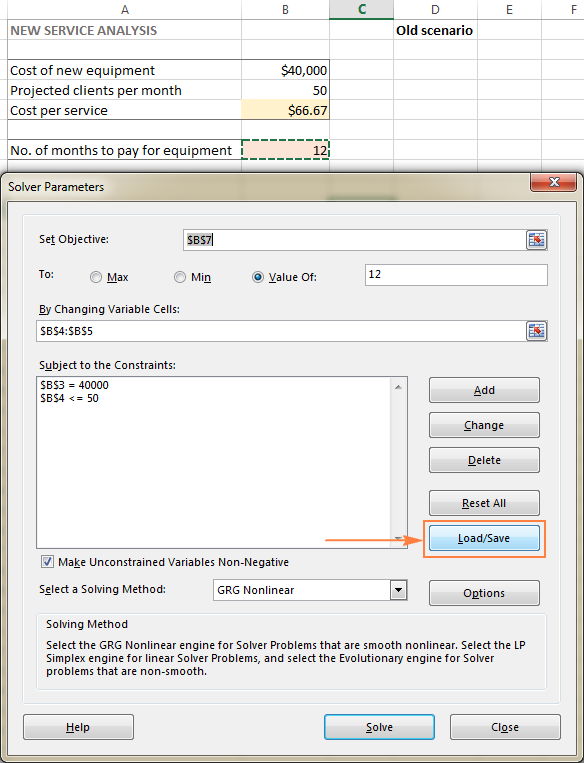
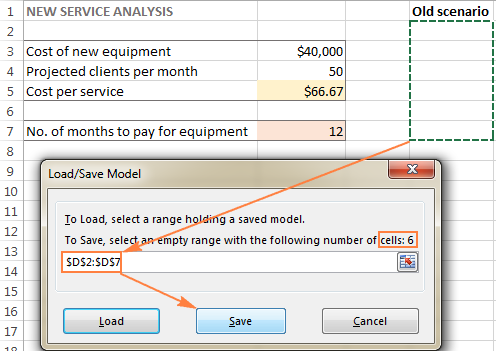
Միևնույն ժամանակ, Solver Parameters պատուհանը կհայտնվի, որտեղ դուք կարող եք փոխել ձեր սահմանափակումները և փորձել տարբեր «ինչ կլիներ, եթե» տարբերակները:
Loading պահպանված մոդելը
Երբ որոշեք վերականգնել պահպանված սցենարը, կատարեք հետևյալը.
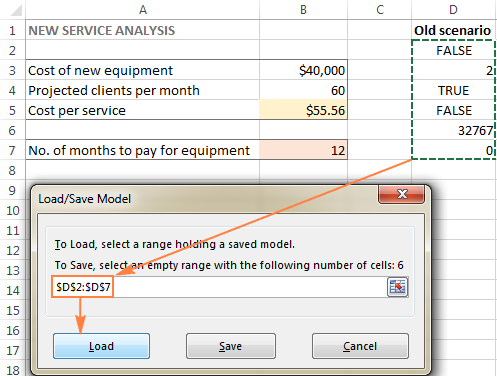
- Լուծիչի պարամետրերը պատուհանում սեղմեք Բեռնել/ Պահպանել կոճակը:
- Աշխատանքային թերթում ընտրեք պահպանված մոդելը պահող բջիջների շրջանակը և սեղմեք Բեռնել :
Excel Solver ալգորիթմներ
Excel Solver-ի համար խնդիր սահմանելիս կարող եք ընտրել Ընտրեք լուծման մեթոդ բացվող վանդակում հետևյալ մեթոդներից մեկը.
- GRG Ոչ գծային: Ընդհանրացված նվազեցված գրադիենտ ոչ գծային ալգորիթմն օգտագործվում է հարթ ոչ գծային խնդիրների համար, այսինքն, որոնցում սահմանափակումներից առնվազն մեկը որոշման փոփոխականների հարթ ոչ գծային ֆունկցիա է: Ավելի մանրամասն կարող եք գտնել այստեղ:
- LP Simplex : Simplex LP Solving մեթոդը հիմնված է Simplex ալգորիթմի վրա, որը ստեղծվել է ամերիկացի մաթեմատիկոս Ջորջ Դանցիգի կողմից: Այն օգտագործվում է այսպես կոչված Գծային ծրագրավորման խնդիրների լուծման համար՝ մաթեմատիկական մոդելներ, որոնց պահանջները բնութագրվում են գծային հարաբերություններով, այսինքն՝ բաղկացած են մեկ նպատակից, որը ներկայացված է գծային հավասարմամբ, որը պետք է առավելագույնի հասցվի կամ նվազագույնի հասցվի։ Լրացուցիչ տեղեկությունների համար այցելեք այս էջը:
- Evolutionary : Այն օգտագործվում է ոչ հարթ խնդիրների համար, որոնք օպտիմալացման խնդիրների լուծման ամենադժվար տեսակն են, քանի որ որոշ գործառույթներ ոչ հարթ կամ նույնիսկ ընդհատվող են, և, հետևաբար, դժվար է որոշել ֆունկցիայի աճի կամ նվազման ուղղությունը: Լրացուցիչ տեղեկությունների համար տես այս էջը:
Որպեսզի լուծումը գտնի լուծումը փոխելու համար սեղմեք Ընտրանքներ կոճակը Լուծիչի պարամետրեր երկխոսության վանդակում, և կարգավորեք ցանկացած կամ բոլոր տարբերակները GRG Nonlinear , All Methods և Evolutionary ներդիրներում:
Այսպես կարող եք օգտագործել Solver-ը Excel-ում: գտնել ձեր որոշումների խնդիրների լավագույն լուծումները: Եվ հիմա, գուցե ցանկանաքներբեռնեք Excel Solver-ի օրինակները, որոնք քննարկվել են այս ձեռնարկում և վերամշակեք դրանք ավելի լավ հասկանալու համար: Ես շնորհակալ եմ կարդալու համար և հուսով եմ, որ հաջորդ շաբաթ կտեսնենք ձեզ մեր բլոգում:
օգնում է ձեզ առավելագույնի հասցնել ներդրումների վերադարձը, ընտրել օպտիմալ բյուջե ձեր գովազդային արշավի համար, կազմել լավագույն աշխատանքային գրաֆիկը ձեր աշխատակիցների համար, նվազագույնի հասցնել առաքման ծախսերը և այլն:Ինչպես ավելացնել Solver-ը Excel-ում
Solver հավելումը ներառված է Microsoft Excel-ի բոլոր տարբերակներում, սկսած 2003թ.-ից, սակայն այն լռելյայն միացված չէ:
Ձեր Excel-ին Solver ավելացնելու համար կատարեք հետևյալ քայլերը.
- Excel 2010 - Excel 365-ում սեղմեք Ֆայլ > Ընտրանքներ :
Excel 2007-ում սեղմեք Microsoft Office կոճակը և ապա սեղմեք Excel Options :
- Excel Options երկխոսության մեջ սեղմեք Add-Ins ձախ կողագոտում, համոզվեք, որ Excel Options 8>Excel-ի հավելումներ ընտրված է պատուհանի ներքևում գտնվող Կառավարել վանդակում և սեղմեք Գնալ :
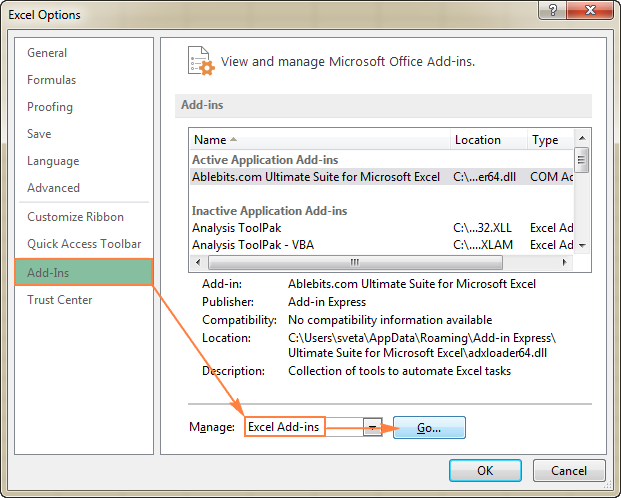
- Տեղում Add-Ins երկխոսության տուփ, ստուգեք Solver Add-in տուփը և սեղմեք OK :
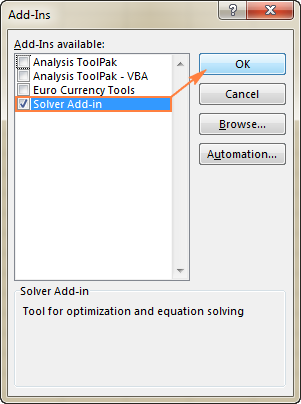
Excel 2003 -ում Solver-ը ստանալու համար գնացեք Գործիքներ ընտրացանկը և սեղմեք Ավելացումներ : Ավելացումներ հասանելի ցանկում նշեք Լրացուցիչ հավելում տուփը և սեղմեք Լավ :
Նշում. Եթե Excel-ը հաղորդագրություն է ցուցադրում, որ Լուծող հավելումը ներկայումս տեղադրված չէ ձեր համակարգչում, սեղմեք Այո այն տեղադրելու համար:
Որտե՞ղ է Solver-ը Excel-ում:
Excel-ի ժամանակակից տարբերակներում Solver կոճակը հայտնվում է Տվյալներ ներդիրում, Վերլուծություն խումբ:

Որտեղ էԼուծու՞մ է Excel 2003-ում:
Excel 2003-ում Solver հավելումը բեռնվելուց հետո նրա հրամանն ավելացվում է Գործիքներ ընտրացանկում.
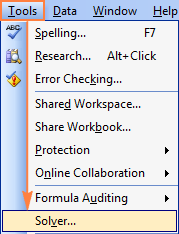
Այժմ, երբ գիտեք, թե որտեղ գտնել Solver-ը Excel-ում, բացեք նոր աշխատաթերթ և եկեք սկսենք:
Նշում: Այս ձեռնարկում քննարկված օրինակները օգտագործում են Solver-ը Excel 2013-ում: Եթե ունեք մեկ այլ Excel տարբերակ, սքրինշոթները կարող են ճիշտ չհամընկնել ձեր տարբերակի հետ, չնայած Solver-ի գործառույթը հիմնականում նույնն է:
Ինչպես օգտագործել Solver-ը Excel-ում
Նախքան Excel Solver հավելումը գործարկելը, ձևակերպեք այն մոդելը, որը ցանկանում եք լուծել աշխատանքային թերթում: Այս օրինակում եկեք լուծում գտնենք օպտիմալացման հետևյալ պարզ խնդրի համար:
Խնդիր : Ենթադրենք, որ դուք գեղեցկության սրահի սեփականատեր եք և նախատեսում եք նոր ծառայություն մատուցել ձեր հաճախորդներին։ Դրա համար դուք պետք է գնեք 40,000 դոլար արժողությամբ նոր սարքավորում, որը պետք է վճարվի ապառիկ 12 ամսվա ընթացքում:
Նպատակը . Հաշվեք յուրաքանչյուր ծառայության նվազագույն արժեքը, որը թույլ կտա ձեզ վճարել դրա համար: նոր սարքավորումները նշված ժամկետներում:
Այս առաջադրանքի համար ես ստեղծել եմ հետևյալ մոդելը.
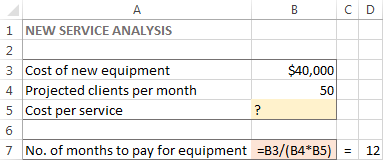
Եվ հիմա, տեսնենք, թե ինչպես կարող է Excel Solver-ը գտնել այս խնդրի լուծումը:
1. Գործարկեք Excel Solver
Տվյալներ ներդիրում, Վերլուծություն խմբում սեղմեք Լուծիչ կոճակը:
2. Սահմանեք խնդիրը
Solver Parameters պատուհանը կբացվի այնտեղ, որտեղ դուք ունեք3 հիմնական բաղադրիչները կարգավորելու համար.
- Օբյեկտիվ բջիջ
- Փոփոխական բջիջներ
- Սահմանափակումներ
Հենց ինչ է անում Excel Solver-ը վերը նշված պարամետրերը. Այն գտնում է բանաձևի օպտիմալ արժեքը (առավելագույնը, նվազագույնը կամ սահմանված) Օբյեկտիվ բջիջում` փոխելով Փոփոխական բջիջների արժեքները և ենթակա է սահմանափակումների Սահմանափակումներում: բջիջներ:
Նպատակ
Նպատակ բջիջը ( Թիրախ բջիջը նախկին Excel տարբերակներում) բանաձև պարունակող բջիջն է որը ներկայացնում է խնդրի նպատակը կամ նպատակը: Նպատակը կարող է լինել առավելագույնի հասցնելը, նվազագույնի հասցնելը կամ որոշակի նպատակային արժեքի հասնելը:
Այս օրինակում նպատակային բջիջը B7 է, որը հաշվարկում է վճարման ժամկետը՝ օգտագործելով =B3/(B4*B5) բանաձևը, և բանաձևի արդյունքը պետք է հավասար լինի 12:
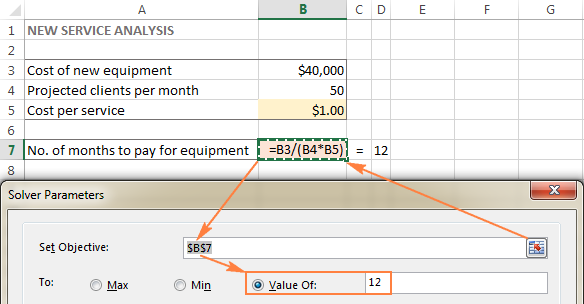
Փոփոխական բջիջներ
Փոփոխական բջիջներ ( Փոփոխվող բջիջներ կամ Կարգավորելի բջիջները ավելի վաղ տարբերակներում) բջիջներ են, որոնք պարունակում են փոփոխական տվյալներ, որոնք կարող են փոփոխվել նպատակին հասնելու համար: Excel Solver-ը թույլ է տալիս նշել մինչև 200 փոփոխական բջիջ:
Այս օրինակում մենք ունենք մի քանի բջիջ, որոնց արժեքները կարող են փոխվել.
- Ամսական կանխատեսվող հաճախորդներ (B4), որոնք պետք է լինի 50-ից փոքր կամ հավասար; և
- Ծառայության արժեքը (B5), որը մենք ցանկանում ենք, որպեսզի Excel Solver-ը հաշվարկի:
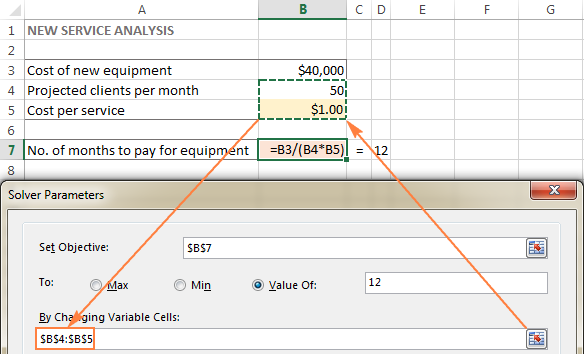
Խորհուրդ. Եթե ձեր մոդելի փոփոխական բջիջները կամ միջակայքերը ոչ հարակից են ,ընտրեք առաջին բջիջը կամ տիրույթը, այնուհետև սեղմեք և պահեք Ctrl ստեղնը՝ ընտրելով այլ բջիջներ և/կամ տիրույթներ: Կամ մուտքագրեք միջակայքերը ձեռքով, բաժանված ստորակետերով:
Սահմանափակումներ
Excel Solver Սահմանափակումները խնդրի հնարավոր լուծումների սահմանափակումներն են կամ սահմանները: Այլ կերպ ասած, սահմանափակումներն այն պայմաններն են, որոնք պետք է կատարվեն:
Սահմանափակ(ներ) ավելացնելու համար կատարեք հետևյալը.
- Սեղմեք Ավելացնել կոճակը դեպի « Ենթակա է սահմանափակումների » վանդակում:
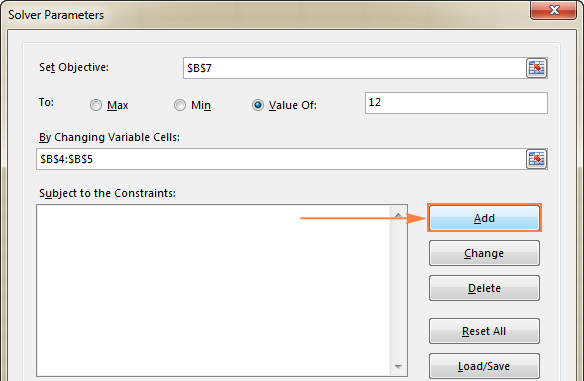
- Սահմանափակում պատուհանում, մուտքագրեք սահմանափակում:
- Սեղմեք Ավելացնել կոճակը` սահմանափակումը ցանկին ավելացնելու համար:
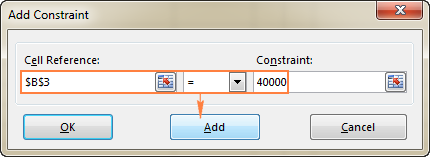
- Շարունակել մուտքագրելով այլ սահմանափակումներ:
- Վերջնական սահմանափակումը մուտքագրելուց հետո սեղմեք OK ` վերադառնալու հիմնական լուծիչ Պարամետրեր պատուհանը:
Excel Solver-ը թույլ է տալիս նշել հետևյալ հարաբերությունները նշված բջիջի և սահմանափակման միջև:
- Պակաս կամ հավասար , հավասար , և մեծ կամ հավասար -ի: Դուք սահմանում եք այս հարաբերությունները՝ ընտրելով բջիջ Բջջի հղում վանդակում, ընտրելով հետևյալ նշաններից մեկը՝ <= , =, կամ > ;= և այնուհետև Սահմանափակում վանդակում մուտքագրեք թիվ, բջջային հղում/բջջի անուն կամ բանաձև (տես վերը նշված սքրինշոթը):
- Ամբողջ թիվ . Եթե հղված բջիջը պետք է լինի ամբողջ թիվ, ընտրեք int ,իսկ ամբողջ թիվ բառը կհայտնվի Սահմանափակում վանդակում։
- Տարբեր արժեքներ ։ Եթե նշված տիրույթի յուրաքանչյուր բջիջ պետք է պարունակի տարբեր արժեք, ընտրեք տարբերակ , և AllDifferent բառը կհայտնվի Սահմանափակում վանդակում:
- Երկուական : Եթե ցանկանում եք սահմանափակել հղված բջիջը 0-ով կամ 1-ով, ընտրեք bin , և երկուական բառը կհայտնվի Սահմանափակում վանդակում:
Ծանոթագրություն. int , bin և dif հարաբերությունները կարող են օգտագործվել միայն փոփոխական բջիջների սահմանափակումների համար:
Գոյություն ունեցող սահմանափակում խմբագրելու կամ ջնջելու կատարեք հետևյալը.
- Solver Parameters երկխոսության վանդակում սեղմեք սահմանափակում:
- Ընտրված սահմանափակումը փոփոխելու համար սեղմեք Փոխել և կատարեք ձեր ուզած փոփոխությունները:
- Սահմանափակումը ջնջելու համար սեղմեք Ջնջել կոճակը: .
Այս օրինակում սահմանափակումներն են.
- B3=40000 - նոր սարքավորումների արժեքը կազմում է $40,000:
- B4<=50 - ամսական կանխատեսվող հիվանդների թիվը մինչև 50:
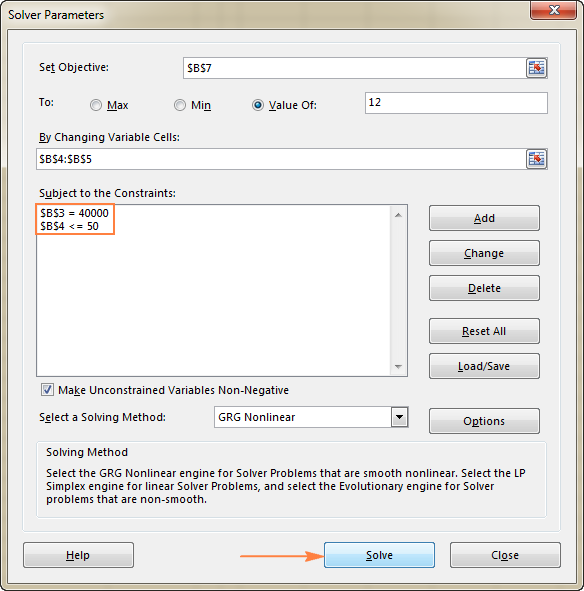
3. Լուծեք խնդիրը
Բոլոր պարամետրերը կազմաձևելուց հետո սեղմեք Լուծել կոճակը Լուծման պարամետրեր պատուհանի ներքևում (տե՛ս վերևի սքրինշոթը) և թույլ տվեք. Excel Solver հավելումը գտնում է ձեր խնդրի օպտիմալ լուծումը:
Կախված մոդելի բարդությունից, համակարգչի հիշողությունից և պրոցեսորի արագությունից, դա կարող է տևել մի քանիսըվայրկյան, մի քանի րոպե կամ նույնիսկ մի քանի ժամ:
Երբ Solver-ը ավարտի մշակումը, այն կցուցադրի Solver Results երկխոսության պատուհանը, որտեղ դուք ընտրում եք Պահպանեք Լուծվող լուծումը և սեղմեք OK :
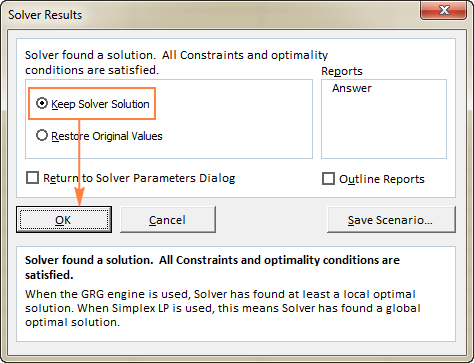
Solver Result պատուհանը կփակվի և լուծումը կհայտնվի աշխատաթերթում անմիջապես:
Այս օրինակում B5 բջիջում հայտնվում է $66,67, որը նվազագույն արժեքն է յուրաքանչյուր ծառայության համար, որը թույլ կտա ձեզ վճարել նոր սարքավորումների համար 12 ամսում, պայմանով, որ յուրաքանչյուրում կա առնվազն 50 հաճախորդ: ամիս՝
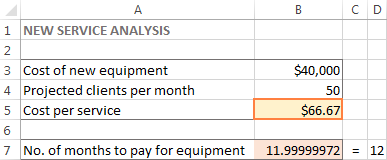
Խորհուրդներ՝
- Եթե Excel Լուծիչը չափազանց երկար է մշակել որոշակի խնդիր, կարող եք ընդհատել գործընթացը՝ սեղմելով Esc բանալի. Excel-ը կվերահաշվարկի աշխատաթերթը Փոփոխական բջիջների համար հայտնաբերված վերջին արժեքներով:
- Լուծված խնդրի մասին ավելի շատ մանրամասներ ստանալու համար սեղմեք հաշվետվության տեսակը Զեկույցներ վանդակում: , ապա սեղմեք OK : Զեկույցը կստեղծվի նոր աշխատաթերթում.
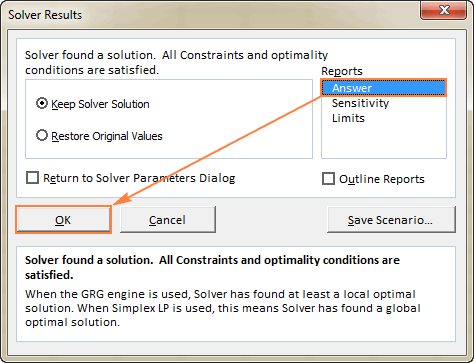
Այժմ, երբ դուք ունեք հիմնական գաղափարը, թե ինչպես օգտագործել Solver-ը Excel-ում, եկեք ավելի սերտ նայենք մի քանիսին: ավելի շատ օրինակներ, որոնք կարող են օգնել ձեզ ավելի շատ պատկերացում կազմել:
Excel Solver-ի օրինակներ
Ստորև դուք կգտնեք Excel Solver հավելման օգտագործման ևս երկու օրինակ: Սկզբում մենք լուծում կգտնենք հայտնի գլուխկոտրուկի համար, իսկ հետո կլուծենք իրական գծային ծրագրավորման խնդիր:
Excel Solver օրինակ 1 (կախարդական քառակուսի)
IՀավատացեք, որ բոլորը ծանոթ են «կախարդական քառակուսի» գլուխկոտրուկներին, որտեղ դուք պետք է մի շարք թվեր տեղադրեք քառակուսու մեջ, որպեսզի բոլոր տողերը, սյունակները և անկյունագծերը գումարվեն որոշակի թվի:
Օրինակ, դուք գիտե՞ք 1-ից 9 թվեր պարունակող 3x3 քառակուսու լուծումը, որտեղ յուրաքանչյուր տող, սյուն և անկյունագծով գումարվում է 15:
Հավանաբար մեծ խնդիր չէ լուծել այս գլուխկոտրուկը փորձի և սխալի միջոցով, բայց ես գրազ կգտնեմ, որ Լուծողը կգտնի: լուծումն ավելի արագ: Աշխատանքի մեր մասը խնդիրը ճիշտ սահմանելն է:
Սկզբից մուտքագրեք 1-ից 9 թվերը 3 տողից և 3 սյունակից բաղկացած աղյուսակում: Excel Solver-ին իրականում այդ թվերը պետք չեն, բայց դրանք մեզ կօգնեն պատկերացնել խնդիրը: Excel Solver հավելյալին իսկապես անհրաժեշտ է SUM բանաձևերը, որոնք կազմում են յուրաքանչյուր տող, սյունակ և 2 շեղանկյուն:
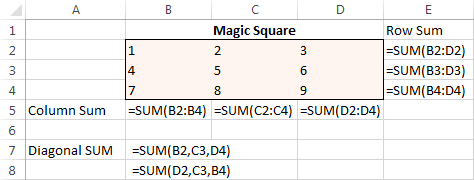
Բոլոր բանաձևերը տեղում գործարկել և կարգավորել Solver հետևյալ պարամետրերը.
- Սահմանել Նպատակ : Այս օրինակում մենք կարիք չունենք որևէ նպատակ դնելու, ուստի այս տուփը դատարկ թողեք:
- Փոփոխական բջիջներ : Մենք ցանկանում ենք թվերը լրացնել B2-ից մինչև D4 բջիջներում, ուստի ընտրեք B2:D4 միջակայքը:
- Սահմանափակումներ : Պետք է բավարարվեն հետևյալ պայմանները՝
- $B$2:$D$4 = AllDifferent - Փոփոխականի բոլոր բջիջները պետք է պարունակեն տարբեր արժեքներ:
- $B$2:$D$4 = ամբողջ թիվ - բոլորը Փոփոխական բջիջները պետք է լինեն ամբողջ թվեր:
- $B$5:$D$5 = 15 - յուրաքանչյուրի արժեքների գումարըսյունակը պետք է հավասար լինի 15-ի:
- $E$2:$E$4 = 15 - յուրաքանչյուր տողի արժեքների գումարը պետք է հավասար լինի 15-ի:
- $B$7:$B$8 = 15 - գումարը երկու անկյունագծերը պետք է հավասար լինեն 15-ի:
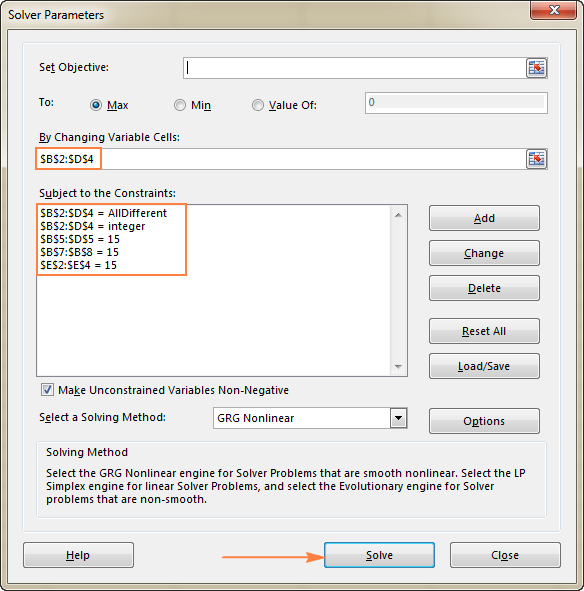
Վերջապես սեղմեք Լուծել կոճակը, և լուծումն այնտեղ է:
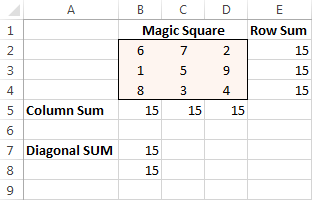
Excel Solver օրինակ 2 (գծային ծրագրավորման խնդիր)
Սա պարզ տրանսպորտային օպտիմալացման խնդրի օրինակ է գծային նպատակով: Այս տեսակի ավելի բարդ օպտիմալացման մոդելներ օգտագործվում են բազմաթիվ ընկերությունների կողմից՝ ամեն տարի հազարավոր դոլարներ խնայելու համար:
Խնդիր . Դուք ցանկանում եք նվազագույնի հասցնել ապրանքների առաքման արժեքը 2 տարբեր պահեստներից մինչև 4 տարբեր: հաճախորդներ. Յուրաքանչյուր պահեստ ունի սահմանափակ առաջարկ, և յուրաքանչյուր հաճախորդ ունի որոշակի պահանջարկ:
Նպատակ . Նվազագույնի հասցնել առաքման ընդհանուր արժեքը՝ չգերազանցելով յուրաքանչյուր պահեստում առկա քանակությունը և բավարարել յուրաքանչյուր հաճախորդի պահանջարկը: .
Աղբյուրի տվյալներ
Ահա, թե ինչպես է երևում մեր տրանսպորտի օպտիմալացման խնդիրը. սահմանեք մեր գծային ծրագրավորման խնդիրը Excel Solver-ի համար, եկեք պատասխանենք 3 հիմնական հարցերին.
- Ի՞նչ որոշումներ պետք է կայացվեն: Մենք ցանկանում ենք հաշվարկել ապրանքների օպտիմալ քանակությունը յուրաքանչյուր հաճախորդին յուրաքանչյուր պահեստից առաքելու համար: Սրանք Փոփոխական բջիջներ են (B7:E8):
- Որո՞նք են սահմանափակումները: Յուրաքանչյուր պահեստում առկա պաշարները (I7:I8) չեն կարող գերազանցվել, և

