Inhoudsopgave
De tutorial legt uit hoe je Solver toevoegt en waar je Solver kunt vinden in verschillende Excel-versies, van 2016 tot 2003. Stap-voor-stap voorbeelden laten zien hoe je Excel Solver kunt gebruiken om optimale oplossingen te vinden voor lineaire programmering en andere soorten problemen.
Iedereen weet dat Microsoft Excel heel wat nuttige functies en krachtige hulpmiddelen bevat die u uren rekenwerk kunnen besparen. Maar wist u dat het ook een hulpmiddel bevat dat u kan helpen optimale oplossingen te vinden voor beslissingsproblemen?
In deze handleiding behandelen we alle essentiële aspecten van de Excel Solver add-in en geven we een stap-voor-stap handleiding voor het meest effectieve gebruik ervan.
Wat is Excel Solver?
Excel Oplosser behoort tot een speciale reeks commando's die vaak What-if Analysis Tools worden genoemd. Het is vooral bedoeld voor simulatie en optimalisatie van diverse bedrijfs- en engineeringmodellen.
De Excel Solver add-in is bijzonder nuttig voor het oplossen van lineaire programmeringsproblemen, ook wel lineaire optimalisatieproblemen genoemd, en wordt daarom soms een lineaire programmeringsoplosser Daarnaast kan het soepele niet-lineaire en niet-vloeiende problemen aan. Zie Excel Solver algoritmen voor meer details.
Hoewel Solver niet elk mogelijk probleem kan oplossen, is het echt nuttig bij allerlei optimalisatieproblemen waarbij u de beste beslissing moet nemen. Het kan u bijvoorbeeld helpen het investeringsrendement te maximaliseren, het optimale budget voor uw reclamecampagne te kiezen, het beste werkschema voor uw werknemers te maken, de leveringskosten te minimaliseren, enzovoort.
Solver toevoegen aan Excel
De invoegtoepassing Solver wordt meegeleverd met alle versies van Microsoft Excel vanaf 2003, maar is niet standaard ingeschakeld.
Voer de volgende stappen uit om Solver toe te voegen aan uw Excel:
- Klik in Excel 2010 - Excel 365 op Bestand > Opties .
In Excel 2007 klikt u op de Microsoft Office knop, en klik dan op Excel-opties .
- In de Excel-opties dialoog, klik op Toevoegingen op de linker zijbalk, zorg ervoor dat Excel-add-ins is geselecteerd in de Beheer vak onderaan het venster, en klik op Ga naar .
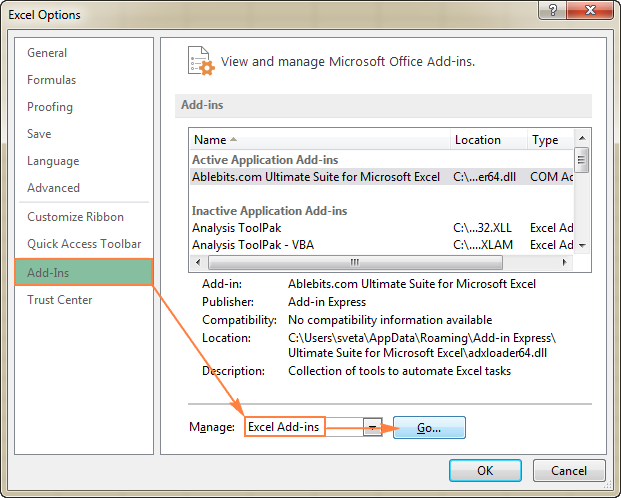
- In de Toevoegingen dialoogvenster, controleer de Oplosser-invoegtoepassing vak, en klik op OK :
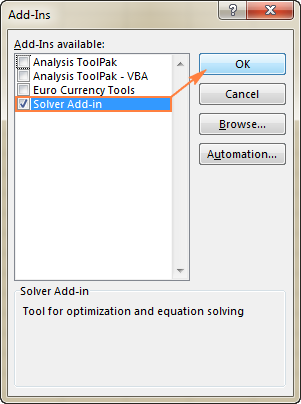
Om Solver aan te zetten Excel 2003 ga naar de Gereedschap menu, en klik op Toevoegingen In de Toevoegingen beschikbaar lijst, controleer de Oplosser-invoegtoepassing en klik op OK .
Opmerking. Als Excel een bericht weergeeft dat de Solver Add-in momenteel niet op uw computer is geïnstalleerd, klikt u op Ja om het te installeren.
Waar is Solver in Excel?
In de moderne versies van Excel is de Oplosser knop verschijnt op de Gegevens tabblad, in de Analyse groep:

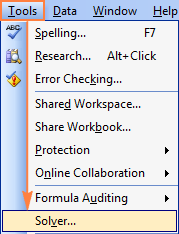
Waar is Solver in Excel 2003?
Nadat de Solver Add-in is geladen in Excel 2003, wordt de opdracht toegevoegd aan de Gereedschap menu:
Nu u weet waar u Solver in Excel kunt vinden, opent u een nieuw werkblad en gaan we aan de slag!
Opmerking. De voorbeelden in deze handleiding gebruiken Solver in Excel 2013. Als u een andere Excel-versie hebt, komen de schermafbeeldingen mogelijk niet exact overeen met uw versie, hoewel de Solver-functionaliteit in principe hetzelfde is.
Hoe Solver gebruiken in Excel
Voordat u de Excel Solver add-in uitvoert, formuleert u het model dat u wilt oplossen in een werkblad. In dit voorbeeld zoeken we een oplossing voor het volgende eenvoudige optimalisatieprobleem.
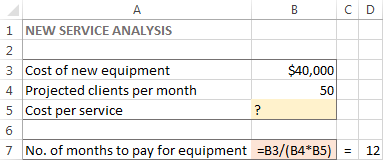
Probleem Stel, u bent eigenaar van een schoonheidssalon en u bent van plan uw klanten een nieuwe dienst aan te bieden. Daarvoor moet u een nieuwe uitrusting kopen die 40.000 dollar kost en die in 12 maanden in termijnen moet worden betaald.
Doel Bereken de minimale kosten per dienst waarmee u de nieuwe apparatuur binnen de gestelde termijn kunt betalen.
Voor deze taak heb ik het volgende model gemaakt:
En laten we nu eens kijken hoe Excel Solver een oplossing kan vinden voor dit probleem.
1. Excel Solver uitvoeren
Op de Gegevens tabblad, in de Analyse groep, klik op de Oplosser knop.
2. Definieer het probleem
De Solverparameters venster wordt geopend waarin u de 3 primaire componenten moet instellen:
- Doelstelling cel
- Variabele cellen
- Beperkingen
Wat doet Excel Solver precies met bovenstaande parameters? Het vindt de optimale waarde (maximum, minimum of opgegeven) voor de formule in het Doelstelling cel door de waarden in de Variabel cellen, en onder voorbehoud van beperkingen in de Beperkingen cellen.
Doelstelling
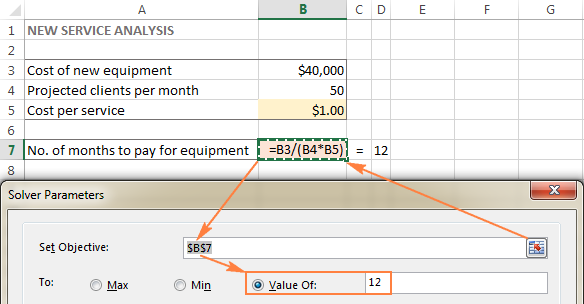
De Doelstelling cel ( Doel cel in eerdere Excel-versies) is de cel die een formule bevat die de doelstelling van het probleem weergeeft. De doelstelling kan zijn: maximaliseren, minimaliseren of een bepaalde streefwaarde bereiken.
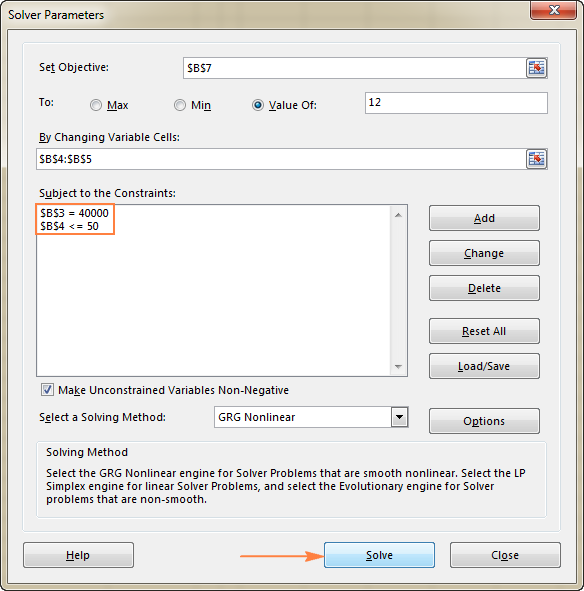
In dit voorbeeld is de objectieve cel B7, die de betalingstermijn berekent met de formule =B3/(B4*B5) en het resultaat van de formule moet gelijk zijn aan 12:
Variabele cellen
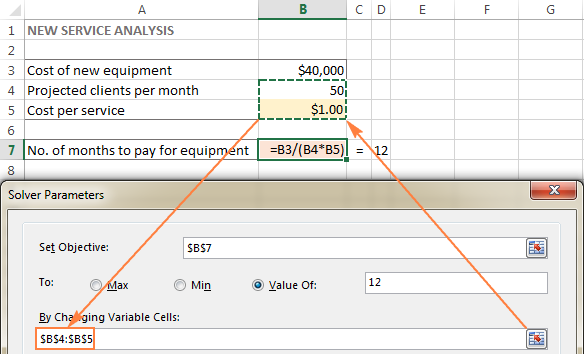
Variabel cellen ( Verandering van cellen of Verstelbaar cellen in eerdere versies) zijn cellen die variabele gegevens bevatten die kunnen worden gewijzigd om het doel te bereiken. Excel Solver staat toe tot 200 variabele cellen op te geven.
In dit voorbeeld hebben we een paar cellen waarvan de waarden kunnen worden veranderd:
- Verwachte cliënten per maand (B4) die minder dan of gelijk moeten zijn aan 50; en
- Kosten per dienst (B5) die we Excel Solver willen laten berekenen.
Tip. Als de variabele cellen of reeksen in uw model niet-aangrenzend Selecteer de eerste cel of het eerste bereik en houd vervolgens de Ctrl-toets ingedrukt terwijl u andere cellen en/of bereiken selecteert. Of typ de bereiken handmatig, gescheiden door komma's.
Beperkingen
De Excel-oplosser Beperkingen zijn beperkingen of limieten van de mogelijke oplossingen van het probleem. Anders gezegd, beperkingen zijn de voorwaarden waaraan moet worden voldaan.
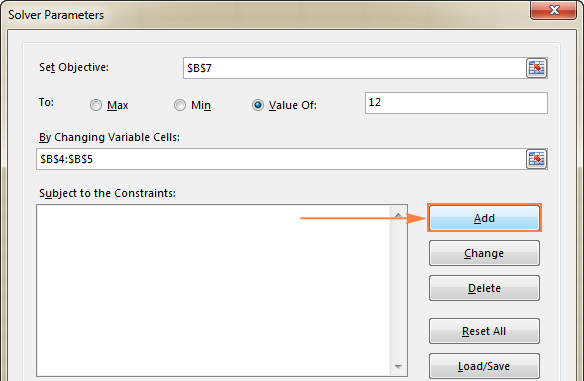
Om een beperking(en) toe te voegen, doet u het volgende:
- Klik op de Toevoegen knop rechts naar de " Onder voorbehoud van de beperkingen "doos.
- In de Beperking venster, voer een beperking in.
- Klik op de Toevoegen om de beperking aan de lijst toe te voegen.
- Ga door met het invoeren van andere beperkingen.
- Nadat u de laatste beperking hebt ingevoerd, klikt u op OK om terug te keren naar de Oplosser Parameters raam.
Excel Solver staat toe de volgende relaties te specificeren tussen de cel waarnaar wordt verwezen en de beperking.
- Minder dan of gelijk aan , gelijk aan en groter dan of gelijk aan U stelt deze relaties in door een cel te selecteren in de Celverwijzing vak, waarbij u een van de volgende tekens kiest: <= , =, of >= en typ vervolgens een getal, celverwijzing/celnaam of formule in het Beperking box (zie bovenstaande schermafbeelding).
- Integer Als de cel waarnaar verwezen wordt een geheel getal moet zijn, selecteer dan int en het woord geheel getal zal verschijnen in de Beperking doos.
- Verschillende waarden Als elke cel in het bereik waarnaar wordt verwezen een andere waarde moet bevatten, selecteert u dif en het woord AllDifferent zal verschijnen in de Beperking doos.
- Binaire Als u een cel waarnaar wordt verwezen wilt beperken tot 0 of 1, selecteert u bin en het woord binair zal verschijnen in de Beperking doos.
Let op. int , bin en dif relaties kunnen alleen worden gebruikt voor beperkingen op Variabele cellen.
Naar edit of verwijder een bestaande beperking doet het volgende:
- In de Solverparameters dialoogvenster, klik op de beperking.
- Om de geselecteerde beperking te wijzigen, klikt u op Verander en breng de gewenste wijzigingen aan.
- Om de beperking te verwijderen, klikt u op de Verwijder knop.
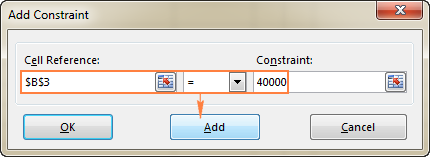
In dit voorbeeld zijn de beperkingen:
- B3=40000 - de kosten van de nieuwe uitrusting bedragen $40.000.
- B4<=50 - het aantal verwachte patiënten per maand in minder dan 50.
3. Het probleem oplossen
Nadat u alle parameters hebt ingesteld, klikt u op de knop Oplossen knop onderaan de Solverparameters venster (zie de schermafbeelding hierboven) en laat de Excel Solver add-in de optimale oplossing voor uw probleem vinden.
Afhankelijk van de complexiteit van het model, het geheugen van de computer en de snelheid van de processor, kan dit enkele seconden, enkele minuten of zelfs enkele uren duren.
Wanneer Solver klaar is met verwerken, toont hij de Resultaten van de oplosser dialoogvenster, waarin u Bewaar de oplossing van de oplosser en klik op OK :
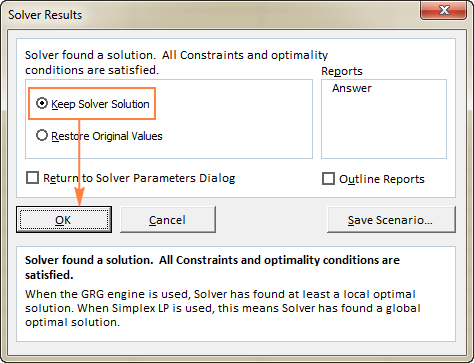
De Oplosser Resultaat venster sluit en de oplossing verschijnt meteen op het werkblad.
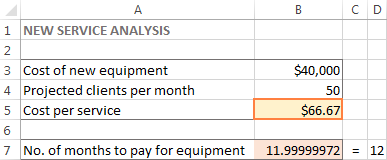
In dit voorbeeld verschijnt 66,67 dollar in cel B5, wat de minimale kosten per dienst zijn waarmee u de nieuwe apparatuur in 12 maanden kunt betalen, mits er minstens 50 klanten per maand zijn:
Tips:
- Indien de Excel Solver een bepaald probleem te lang heeft verwerkt, kunt u het proces onderbreken door op de Esc-toets te drukken. Excel zal het werkblad opnieuw berekenen met de laatst gevonden waarden voor de Variabel cellen.
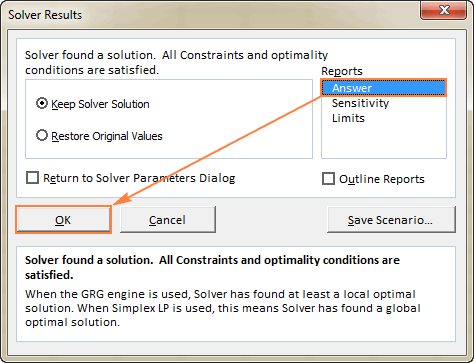
- Voor meer details over het opgeloste probleem klikt u op een rapporttype in het Rapporten en klik dan op OK Het rapport wordt aangemaakt op een nieuw werkblad:
Nu u het basisidee hebt van het gebruik van Solver in Excel, laten we nog een paar voorbeelden bekijken die u kunnen helpen meer inzicht te krijgen.
Excel Solver voorbeelden
Hieronder vindt u nog twee voorbeelden van het gebruik van de Excel Solver addin. Eerst zoeken we een oplossing voor een bekende puzzel, en vervolgens lossen we een echt lineair programmeringsprobleem op.
Excel Solver voorbeeld 1 (magisch vierkant)
Ik denk dat iedereen bekend is met "magisch vierkant" puzzels waarbij je een reeks getallen in een vierkant moet plaatsen zodat alle rijen, kolommen en diagonalen optellen tot een bepaald getal.
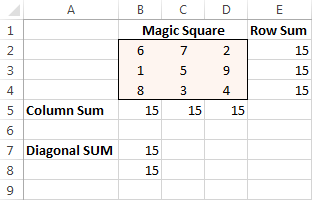
Weet u bijvoorbeeld een oplossing voor het 3x3 vierkant met getallen van 1 tot 9 waarbij elke rij, kolom en diagonaal opgeteld 15 is?
Het is waarschijnlijk niet erg om deze puzzel met vallen en opstaan op te lossen, maar ik wed dat de oplosser de oplossing sneller vindt. Ons deel van de taak is het probleem goed te definiëren.
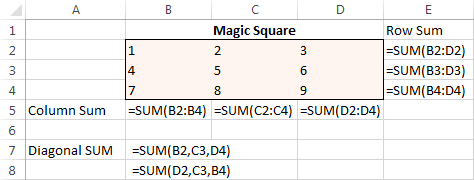
Om te beginnen voert u de getallen van 1 tot 9 in een tabel in die bestaat uit 3 rijen en 3 kolommen. De Excel Solver heeft deze getallen eigenlijk niet nodig, maar ze helpen ons het probleem te visualiseren. Wat de Excel Solver add-in echt nodig heeft zijn de SUM formules die elke rij, kolom en 2 diagonalen optellen:
Als alle formules klaar zijn, voert u Solver uit en stelt u de volgende parameters in:
- Stel Doelstelling In dit voorbeeld hoeven we geen doelstelling in te stellen, dus laten we dit vakje leeg.
- Variabele cellen We willen getallen invullen in de cellen B2 tot en met D4, dus selecteer het bereik B2:D4.
- Beperkingen Aan de volgende voorwaarden moet worden voldaan:
- $B$2:$D$4 = AllDifferent - alle variabele cellen moeten verschillende waarden bevatten.
- $B$2:$D$4 = geheel getal - alle variabele cellen moeten gehele getallen zijn.
- $B$5:$D$5 = 15 - de som van de waarden in elke kolom moet gelijk zijn aan 15.
- $E$2:$E$4 = 15 - de som van de waarden in elke rij moet gelijk zijn aan 15.
- $B$7:$B$8 = 15 - de som van beide diagonalen moet gelijk zijn aan 15.
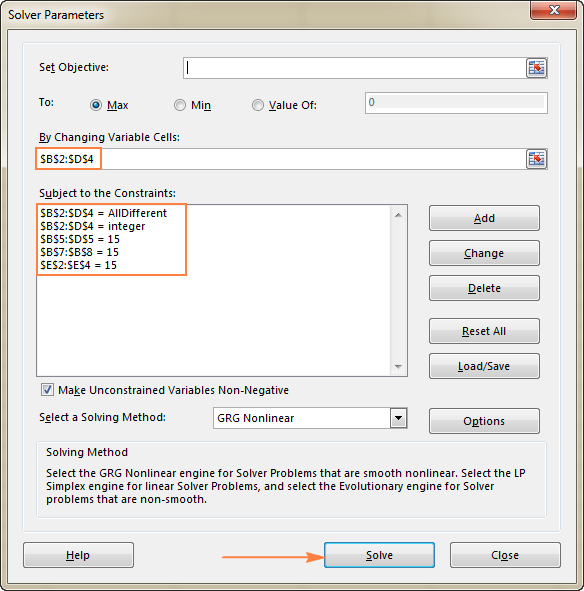
Klik ten slotte op de Oplossen knop, en de oplossing is er!
Excel Solver voorbeeld 2 (lineair programmeringsprobleem)
Dit is een voorbeeld van een eenvoudig transportoptimalisatieprobleem met een lineaire doelstelling. Dergelijke complexere optimalisatiemodellen worden door veel bedrijven gebruikt om jaarlijks duizenden dollars te besparen.
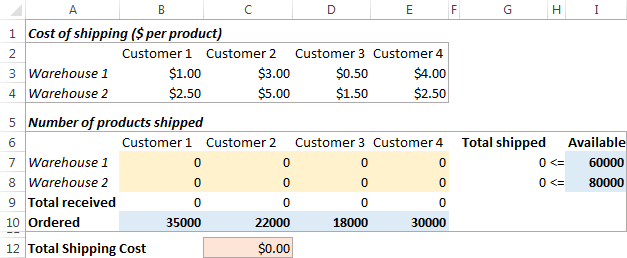
Probleem U wilt de kosten van het verzenden van goederen van 2 verschillende magazijnen naar 4 verschillende klanten minimaliseren. Elk magazijn heeft een beperkte voorraad en elke klant heeft een bepaalde vraag.
Doel : De totale verzendkosten minimaliseren, de in elk magazijn beschikbare hoeveelheid niet overschrijden en aan de vraag van elke klant voldoen.
Bron gegevens
Zo ziet ons transportoptimalisatieprobleem eruit:
Het model formuleren
Om ons lineaire programmeringsprobleem voor de Excel Solver te definiëren, laten we de 3 hoofdvragen beantwoorden:
- Welke beslissingen moeten worden genomen? Wij willen de optimale hoeveelheid goederen berekenen om aan elke klant te leveren vanuit elk magazijn. Deze zijn Variabel cellen (B7:E8).
- Wat zijn de beperkingen? De in elk magazijn beschikbare voorraden (I7:I8) mogen niet worden overschreden, en de door elke klant bestelde hoeveelheid (B10:E10) moet worden geleverd. Dit zijn Beperkt cellen.
- Wat is het doel? De minimale totale kosten van verzending. En dit is onze Doelstelling cel (C12).
Het volgende dat u moet doen, is de totale hoeveelheid die vanuit elk magazijn is verzonden (G7:G8), en de totale hoeveelheid goederen die door elke klant is ontvangen (B9:E9) berekenen. U kunt dit doen met eenvoudige somformules die in de onderstaande schermafbeelding worden getoond. Voeg ook de SUMPRODUCT-formule in C12 in om de totale verzendkosten te berekenen:
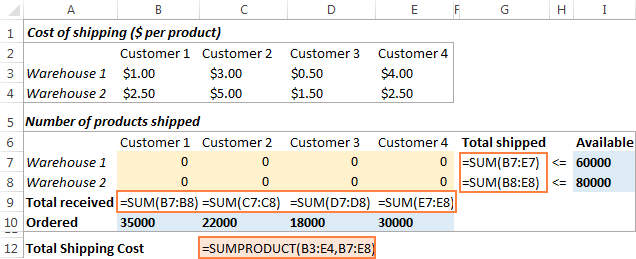
Om ons transportoptimalisatiemodel begrijpelijker te maken, maken we de volgende reeksen met een naam:
| Naam van het bereik | Cellen | Oplosparameter |
| Producten_verzonden | B7:E8 | Variabele cellen |
| Beschikbaar | I7:I8 | Beperking |
| Totaal_verzonden | G7:G8 | Beperking |
| Besteld | B10:E10 | Beperking |
| Totaal_ontvangen | B9:E9 | Beperking |
| Verzendkosten | C12 | Doelstelling |
Het laatste wat u nog moet doen is de Excel Solver parameters configureren:
- Doelstelling: Verzendkosten ingesteld op Min
- Variabele cellen: Products_shipped
- Restricties: Totaal_ontvangen = Besteld en Totaal_verzonden <= Beschikbaar
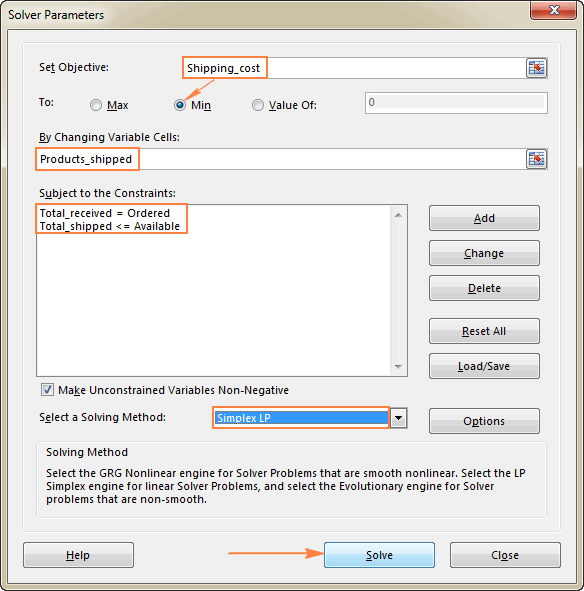
Let erop dat we de Simplex LP oplossingsmethode in dit voorbeeld omdat we te maken hebben met een lineair programmeringsprobleem. Als u niet zeker weet wat voor soort probleem het uwe is, kunt u de standaardinstelling GRG Niet-lineair Voor meer informatie, zie Excel Solver algoritmen.
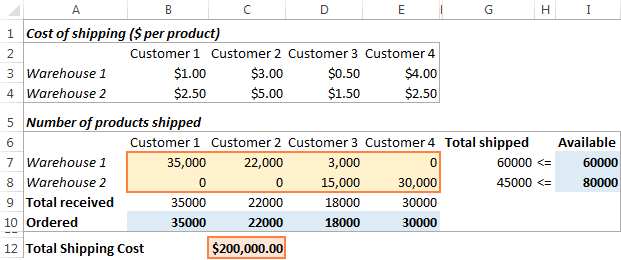
Oplossing
Klik op de Oplossen knop onderaan de Solverparameters In dit voorbeeld berekende de Excel Solver add-in de optimale hoeveelheid goederen om aan elke klant te leveren vanuit elk magazijn met de minimale totale verzendkosten:
Hoe Excel Solver scenario's opslaan en laden
Bij het oplossen van een bepaald model wilt u misschien uw Variabel celwaarden als een scenario dat u later kunt bekijken of hergebruiken.
Bijvoorbeeld, bij het berekenen van de minimale servicekosten in het allereerste voorbeeld dat in deze handleiding wordt besproken, wilt u misschien verschillende aantallen geprojecteerde klanten per maand proberen en kijken hoe dat de servicekosten beïnvloedt. Daarbij wilt u misschien het meest waarschijnlijke scenario dat u al hebt berekend opslaan en op elk moment weer herstellen.
Besparing een Excel Solver scenario komt neer op het selecteren van een cellenbereik om de gegevens in op te slaan. Laden een Solver-model is gewoon een kwestie van Excel voorzien van het cellenbereik waarin uw model is opgeslagen. De gedetailleerde stappen volgen hieronder.
Het model opslaan
Voer de volgende stappen uit om het Excel Solver scenario op te slaan:
- Open het werkblad met het berekende model en voer de Excel Solver uit.
- In de Solverparameters venster, klik op de Laden/opslaan knop.
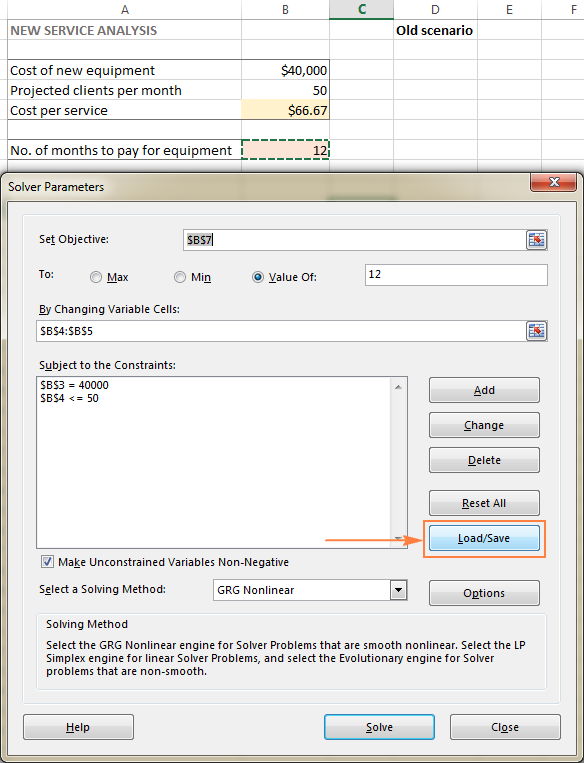
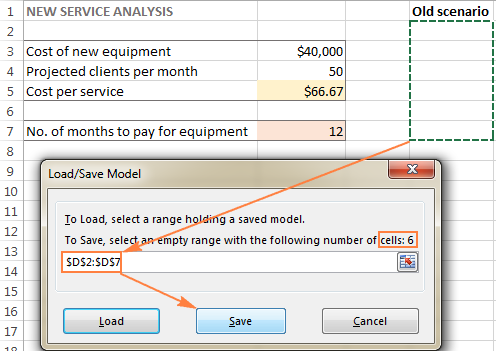
Tegelijkertijd is de Solverparameters verschijnt een venster waarin u uw beperkingen kunt wijzigen en verschillende "wat als"-opties kunt proberen.
Laden van het opgeslagen model
Wanneer u besluit het opgeslagen scenario te herstellen, doet u het volgende:
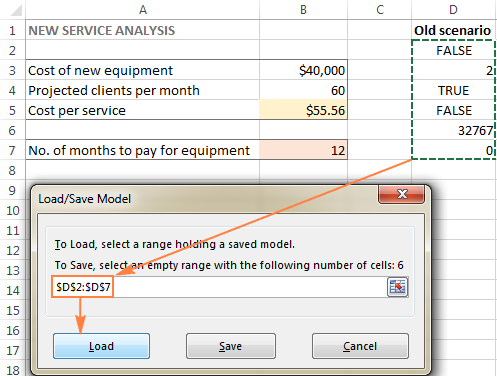
- In de Solverparameters venster, klik op de Laden/opslaan knop.
- Selecteer in het werkblad het cellenbereik met het opgeslagen model en klik op Belasting :
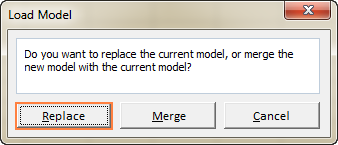
Excel Solver algoritmen
Wanneer u een probleem definieert voor de Excel Solver, kunt u een van de volgende methoden kiezen in de Selecteer een oplosmethode dropdown box:
- GRG Nonlineair. Gegeneraliseerde verminderde gradiënt niet-lineair algoritme wordt gebruikt voor problemen die glad niet-lineair zijn, d.w.z. waarbij ten minste één van de beperkingen een gladde niet-lineaire functie van de beslissingsvariabelen is. Meer details vindt u hier.
- LP Simplex De Simplex LP oplosmethode is gebaseerd op het Simplex-algoritme van de Amerikaanse wiskundige George Dantzig. Het wordt gebruikt voor het oplossen van zgn. Lineair Programmeren problemen - wiskundige modellen waarvan de vereisten worden gekenmerkt door lineaire verbanden, d.w.z. bestaan uit één enkele doelstelling, vertegenwoordigd door een lineaire vergelijking die moet worden gemaximaliseerd of geminimaliseerd. Voor meer informatie, zie deze pagina.
- Evolutionair Het wordt gebruikt voor niet-vloeiende problemen, de moeilijkste soort optimalisatieproblemen om op te lossen, omdat sommige functies niet-vloeiend of zelfs discontinu zijn, en het daarom moeilijk is te bepalen in welke richting een functie toe- of afneemt. Zie voor meer informatie deze pagina.
Om te veranderen hoe Solver een oplossing vindt, klikt u op de knop Opties knop in de Solverparameters dialoogvenster, en configureer één of alle opties op de GRG Niet-lineair , Alle methoden en Evolutionair tabbladen.
Dit is hoe u Solver in Excel kunt gebruiken om de beste oplossingen te vinden voor uw besluitvormingsproblemen. En nu kunt u misschien de Excel Solver voorbeelden die in deze tutorial zijn besproken downloaden en terugdraaien voor een beter begrip. Ik dank u voor het lezen en hoop u volgende week op onze blog te zien.

