Indholdsfortegnelse
Vejledningen forklarer, hvordan du tilføjer og hvor du finder Solver i forskellige Excel-versioner, fra 2016 til 2003. Trin-for-trin eksempler viser, hvordan du bruger Excel Solver til at finde optimale løsninger til lineær programmering og andre typer problemer.
Alle ved, at Microsoft Excel indeholder en masse nyttige funktioner og kraftfulde værktøjer, der kan spare dig for mange timers beregninger. Men vidste du, at det også indeholder et værktøj, der kan hjælpe dig med at finde optimale løsninger på beslutningsproblemer?
I denne vejledning vil vi dække alle væsentlige aspekter af Excel Solver-tilføjelsesprogrammet og give en trin-for-trin-guide til, hvordan du bruger det mest effektivt.
Hvad er Excel Solver?
Excel Solver hører til et særligt sæt kommandoer, der ofte kaldes What-if Analysis Tools, og som primært er beregnet til simulering og optimering af forskellige forretnings- og tekniske modeller.
Excel Solver-tilføjelsesprogrammet er især nyttigt til løsning af lineære programmeringsproblemer, også kaldet lineære optimeringsproblemer, og kaldes derfor nogle gange en lineær programmeringsløser Derudover kan den håndtere glatte ikke-lineære og ikke-godtflydende problemer. Se Excel Solver-algoritmer for flere oplysninger.
Selv om Solver ikke kan løse alle mulige problemer, er det virkelig nyttigt, når du skal løse alle former for optimeringsproblemer, hvor du skal træffe den bedste beslutning. Det kan f.eks. hjælpe dig med at maksimere investeringsafkastet, vælge det optimale budget for din reklamekampagne, lave den bedste arbejdstidsplan for dine medarbejdere, minimere leveringsomkostningerne osv.
Sådan tilføjer du Solver til Excel
Add-in'et Solver er inkluderet i alle versioner af Microsoft Excel fra 2003, men det er ikke aktiveret som standard.
For at tilføje Solver til din Excel skal du udføre følgende trin:
- I Excel 2010 - Excel 365 skal du klikke på Fil > Indstillinger .
I Excel 2007 skal du klikke på Microsoft Office knappen, og klik derefter på Excel-muligheder .
- I den Excel-muligheder dialogboksen, skal du klikke på Tilføjelser på venstre sidepanel, skal du sørge for, at Excel-tilføjelser er valgt i den Administrer nederst i vinduet, og klik på Gå .
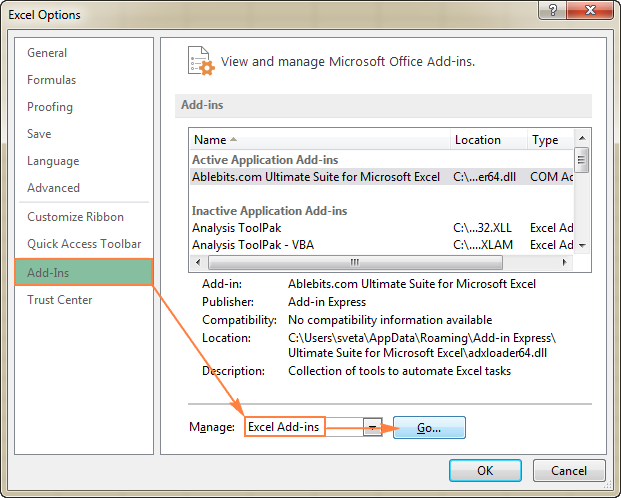
- I den Tilføjelser dialogboksen, markerer du Solver Add-in feltet, og klik på OK :
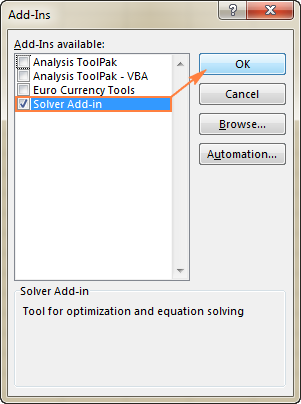
Sådan får du Solver på Excel 2003 , gå til Værktøj menuen, og klik på Tilføjelser . I den Tilføjelser tilgængelig listen, skal du kontrollere Solver Add-in feltet, og klik på OK .
Bemærk. Hvis Excel viser en meddelelse om, at Solver Add-in'en ikke er installeret på din computer, skal du klikke på Ja for at installere det.
Hvor er Solver i Excel?
I de moderne versioner af Excel er Løser vises på knappen Data under fanen, i fanen Analyse gruppe:

Hvor er Solver i Excel 2003?
Når Solver Add-in'en er indlæst i Excel 2003, tilføjes dens kommando til Værktøj menu:
Nu hvor du ved, hvor du kan finde Solver i Excel, skal du åbne et nyt regneark og komme i gang!
Bemærk: Eksemplerne i denne vejledning bruger Solver i Excel 2013. Hvis du har en anden Excel-version, passer skærmbillederne muligvis ikke helt til din version, selv om Solver-funktionerne grundlæggende er de samme.
Sådan bruger du Solver i Excel
Før du kører Excel Solver add-in'en, skal du formulere den model, du vil løse, i et regneark. I dette eksempel skal vi finde en løsning på følgende enkle optimeringsproblem.
Problem Hvis du er ejer af en skønhedssalon, og du planlægger at tilbyde dine kunder en ny service, skal du købe et nyt udstyr til 40.000 USD, som skal betales i afdrag inden for 12 måneder.
Mål : Beregn den minimale omkostning pr. service, så du kan betale for det nye udstyr inden for den angivne tidsramme.
Til denne opgave har jeg oprettet følgende model:
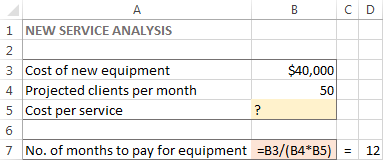
Og lad os nu se, hvordan Excel Solver kan finde en løsning på dette problem.
1. Kør Excel Solver
På den Data under fanen, i fanen Analyse gruppe, skal du klikke på Løser knap.
2. Definer problemet
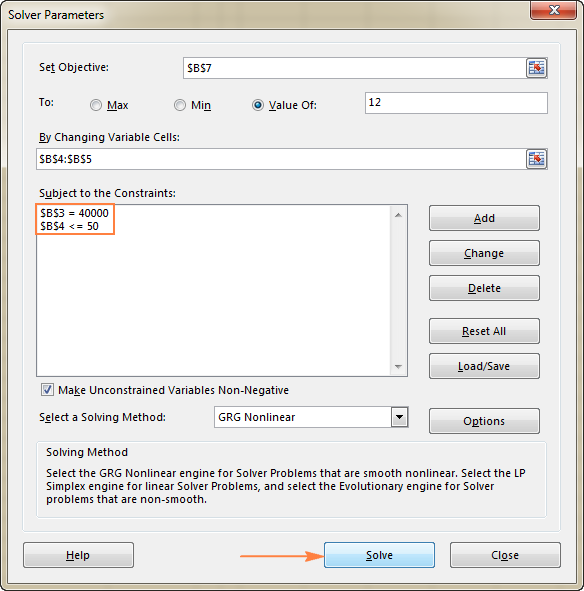
Parametre for opløseren åbnes et vindue, hvor du skal indstille de 3 primære komponenter:
- Objektiv celle
- Variable celler
- Begrænsninger
Hvad gør Excel Solver præcist med ovenstående parametre? Den finder den optimale værdi (maksimum, minimum eller angivet) for formlen i Målsætning celle ved at ændre værdierne i Variabel celler, og med forbehold af begrænsninger i den Begrænsninger celler.
Målsætning
Målsætning celle ( Mål celle i tidligere Excel-versioner) er den celle med en formel der repræsenterer problemets mål eller målsætning. Målet kan være at maksimere, minimere eller opnå en bestemt målværdi.
I dette eksempel er målcellen B7, som beregner betalingsbetingelsen ved hjælp af formlen =B3/(B4*B5) og resultatet af formlen skal være lig med 12:
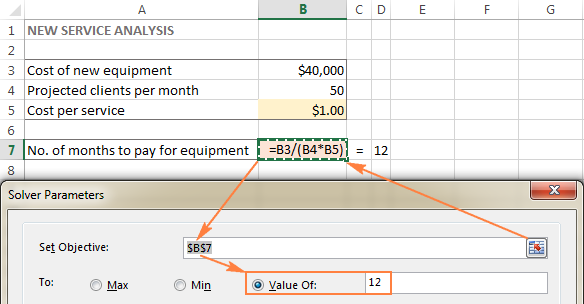
Variable celler
Variabel celler ( Ændring af celler eller Justerbar celler i tidligere versioner) er celler, der indeholder variable data, som kan ændres for at nå målet. Excel Solver giver mulighed for at angive op til 200 variable celler.
I dette eksempel har vi et par celler, hvis værdier kan ændres:
- Forventede kunder pr. måned (B4), som skal være mindre end eller lig med 50, og
- Omkostninger pr. tjeneste (B5), som vi ønsker, at Excel Solver skal beregne.
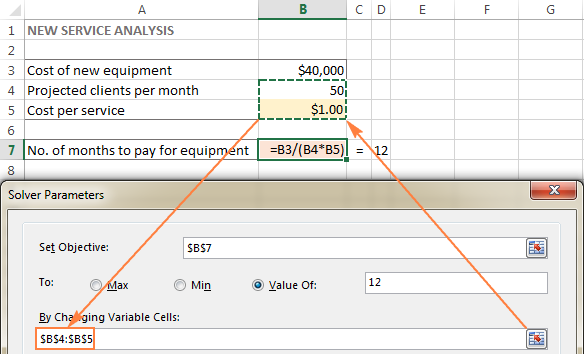
Tip. Hvis de variable celler eller intervaller i din model er ikke-tilstødende , vælg den første celle eller det første område, og hold derefter Ctrl-tasten nede, mens du markerer andre celler og/eller områder. Du kan også skrive områderne manuelt, adskilt med kommaer.
Begrænsninger
Excel Solver Begrænsninger er begrænsninger eller grænser for de mulige løsninger på problemet. Med andre ord er begrænsninger de betingelser, der skal være opfyldt.
Gør følgende for at tilføje en eller flere begrænsninger:
- Klik på den Tilføj knappen til højre for " Under forudsætning af de begrænsninger " boks.
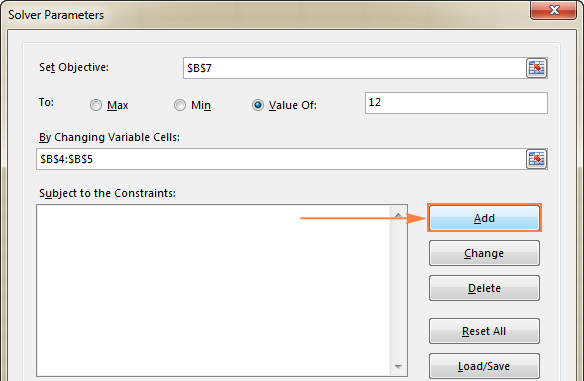
- I den Begrænsning vinduet, skal du indtaste en begrænsning.
- Klik på den Tilføj knappen for at tilføje begrænsningen til listen.
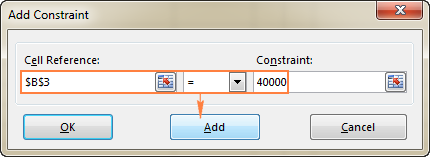
- Fortsæt med at indtaste andre begrænsninger.
- Når du har indtastet den sidste begrænsning, skal du klikke på OK for at vende tilbage til hovedskærmen Løser Parametre vindue.
Excel Solver giver mulighed for at angive følgende relationer mellem den refererede celle og begrænsningen.
- Mindre end eller lig med , er lig med , og er større end eller lig med Du indstiller disse relationer ved at vælge en celle i Celle reference feltet, og vælg et af følgende tegn: <= , =, eller >= , og skriv derefter et tal, en cellehenvisning/cellenavn eller en formel i feltet Begrænsning feltet (se ovenstående skærmbillede).
- Hele tal Hvis den celle, der henvises til, skal være et heltal, skal du vælge int , og ordet heltal vil blive vist i Begrænsning boks.
- Forskellige værdier Hvis hver celle i det refererede område skal indeholde en anden værdi, skal du vælge dif , og ordet Alleforskellige vil blive vist i Begrænsning boks.
- Binær Hvis du vil begrænse en celle, der henvises til, til enten 0 eller 1, skal du vælge bin , og ordet binær vil blive vist i Begrænsning boks.
Bemærk. int , bin , og dif relationer kan kun bruges til begrænsninger på variable celler.
Til redigere eller slet en eksisterende begrænsning gøre følgende:
- I den Parametre for opløseren dialogboksen, klik på begrænsningen.
- Hvis du vil ændre den valgte begrænsning, skal du klikke på Ændre og foretage de ønskede ændringer.
- Hvis du vil slette begrænsningen, skal du klikke på Slet knap.
I dette eksempel er begrænsningerne følgende:
- B3=40000 - prisen for det nye udstyr er 40.000 $.
- B4<=50 - antallet af forventede patienter pr. måned under 50.
3. Løs problemet
Når du har konfigureret alle parametrene, skal du klikke på Løs knappen nederst på Parametre for opløseren vinduet (se skærmbilledet ovenfor) og lad Excel Solver add-in'en finde den optimale løsning til dit problem.
Afhængigt af modellens kompleksitet, computerens hukommelse og processorhastighed kan det tage et par sekunder, et par minutter eller endda et par timer.
Når Solver er færdig med behandlingen, vises Resultater af opløseren dialogvindue, hvor du vælger Behold Solver-løsningen og klik på OK :
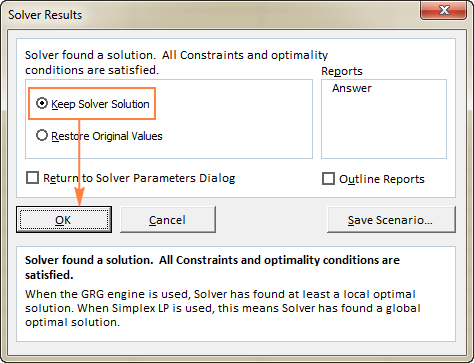
Solver Resultat vinduet lukkes, og løsningen vises på regnearket med det samme.
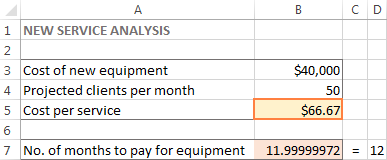
I dette eksempel vises 66,67 $ i celle B5, hvilket er den minimale omkostning pr. service, som gør det muligt at betale for det nye udstyr på 12 måneder, forudsat at der er mindst 50 kunder om måneden:
Tips:
- Hvis Excel Solver har behandlet et bestemt problem for længe, kan du afbryde processen ved at trykke på Esc-tasten. Excel vil genberegne regnearket med de sidste værdier, der er fundet for det pågældende problem. Variabel celler.
- Hvis du vil have flere oplysninger om det løste problem, skal du klikke på en rapporttype i Rapporter feltet, og klik derefter på OK Rapporten oprettes på et nyt regneark:
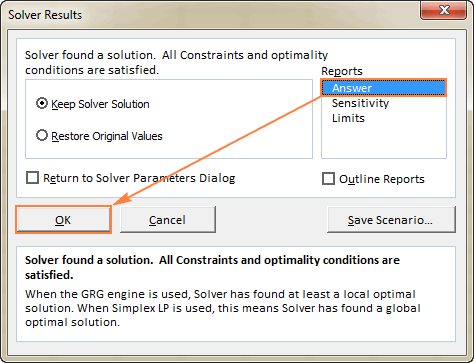
Nu hvor du har fået den grundlæggende idé om, hvordan du bruger Solver i Excel, kan vi se nærmere på et par eksempler, der kan hjælpe dig med at få en bedre forståelse.
Excel Solver eksempler
Nedenfor finder du yderligere to eksempler på brugen af Excel Solver addin. Først finder vi en løsning på et velkendt puslespil, og derefter løser vi et virkeligt lineært programmeringsproblem.
Excel Solver eksempel 1 (magisk kvadrat)
Jeg tror, at alle kender de såkaldte "magiske firkanter", hvor man skal lægge et sæt tal i en firkant, så alle rækker, kolonner og diagonaler summerer til et bestemt tal.
Kender du f.eks. en løsning til 3x3 kvadratet med tal fra 1 til 9, hvor hver række, kolonne og diagonal giver 15?
Det er sikkert ikke noget problem at løse dette puslespil ved at prøve sig frem, men jeg vil vædde på, at Solver finder løsningen hurtigere. Vores del af opgaven er at definere problemet korrekt.
Til at begynde med skal du indtaste tallene fra 1 til 9 i en tabel bestående af 3 rækker og 3 kolonner. Excel Solver har faktisk ikke brug for disse tal, men de vil hjælpe os med at visualisere problemet. Hvad Excel Solver-tilføjelsesprogrammet virkelig har brug for, er SUM-formlerne, der summerer hver række, kolonne og 2 diagonaler:
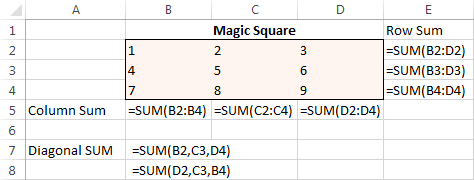
Når alle formlerne er på plads, skal du køre Solver og indstille følgende parametre:
- Indstil Målsætning I dette eksempel behøver vi ikke at angive noget mål, så lad dette felt være tomt.
- Variable celler Vi ønsker at udfylde tal i cellerne B2 til D4, så vælg området B2:D4.
- Begrænsninger Følgende betingelser skal være opfyldt:
- $B$2:$D$4 = AllDifferent - alle Variable-cellerne skal indeholde forskellige værdier.
- $B$2:$D$4 = heltal - alle Variable-cellerne skal være hele tal.
- $B$5:$D$5 = 15 - summen af værdierne i hver kolonne skal være lig med 15.
- $E$2:$E$4 = 15 - summen af værdierne i hver række skal være lig med 15.
- $B$7:$B$8 = 15 - summen af begge diagonaler skal være lig med 15.
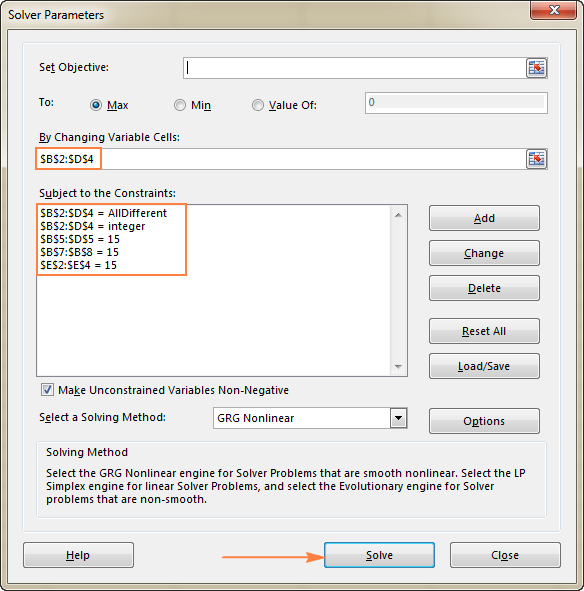
Endelig skal du klikke på Løs knappen, og løsningen er der!
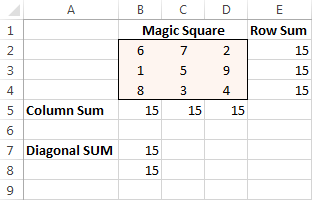
Excel Solver eksempel 2 (problem med lineær programmering)
Dette er et eksempel på et simpelt transportoptimeringsproblem med et lineært mål. Mere komplekse optimeringsmodeller af denne type bruges af mange virksomheder til at spare tusindvis af dollars hvert år.
Problem : Du ønsker at minimere omkostningerne ved at sende varer fra 2 forskellige lagre til 4 forskellige kunder. Hvert lager har et begrænset udbud, og hver kunde har en bestemt efterspørgsel.
Mål : Minimere de samlede forsendelsesomkostninger, uden at overskride den mængde, der er til rådighed på hvert lager, og imødekomme hver enkelt kundes efterspørgsel.
Kildeoplysninger
Sådan ser vores transportoptimeringsproblem ud:
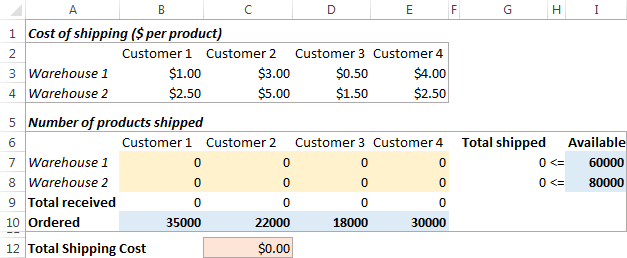
Formulering af modellen
For at definere vores lineære programmeringsproblem for Excel Solver skal vi besvare de 3 hovedspørgsmål:
- Hvilke beslutninger skal der træffes? Vi ønsker at beregne den optimale mængde varer, der skal leveres til hver kunde fra hvert lager. Disse er Variabel celler (B7:E8).
- Hvad er begrænsningerne? De disponible forsyninger på hvert lager (I7:I8) må ikke overskrides, og den mængde, som hver kunde har bestilt (B10:E10), skal leveres. Disse er Begrænset celler .
- Hvad er målet? Minimale samlede forsendelsesomkostninger. Og det er vores Målsætning celle (C12).
Det næste, du skal gøre, er at beregne den samlede mængde, der er afsendt fra hvert lager (G7:G8), og de samlede varer, som hver kunde har modtaget (B9:E9). Du kan gøre dette med enkle sumformler som vist i nedenstående skærmbillede. Indsæt også SUMPRODUCT-formlen i C12 for at beregne de samlede forsendelsesomkostninger:
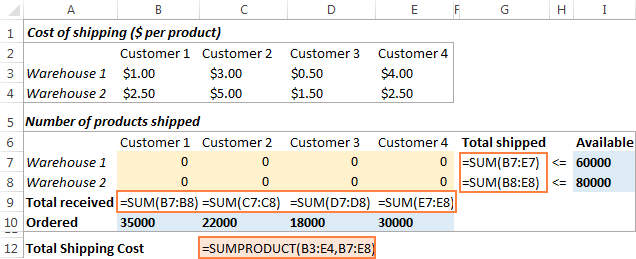
For at gøre vores transportoptimeringsmodel lettere at forstå, opretter vi følgende navngivne områder:
| Område navn | Celler | Parameter for opløseren |
| Products_shipped | B7:E8 | Variable celler |
| Tilgængelig | I7:I8 | Begrænsning |
| Total_shipped | G7:G8 | Begrænsning |
| Bestilt | B10:E10 | Begrænsning |
| I alt_modtaget | B9:E9 | Begrænsning |
| Forsendelsesomkostninger | C12 | Målsætning |
Det sidste, du skal gøre, er at konfigurere Excel Solver-parametrene:
- Formål: Shipping_cost sat til Min
- Variable celler: Products_shipped
- Begrænsninger: Total_received = Bestilt og Total_shipped <= Tilgængelig
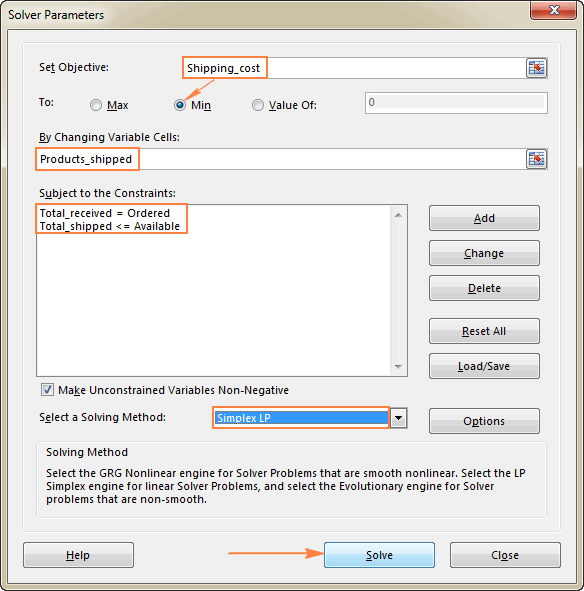
Vær venligst opmærksom på, at vi har valgt den Simplex LP løsningsmetode i dette eksempel, fordi vi har at gøre med et lineært programmeringsproblem. Hvis du ikke er sikker på, hvilken type problem dit er, kan du lade standardindstillingen GRG Ikke-lineær Du kan finde flere oplysninger under Excel Solver-algoritmer.
Løsning
Klik på den Løs knappen nederst på Parametre for opløseren I dette eksempel beregnede Excel Solver-tilføjelsesprogrammet den optimale mængde varer, der skal leveres til hver kunde fra hvert lager med de mindste samlede omkostninger til forsendelse:
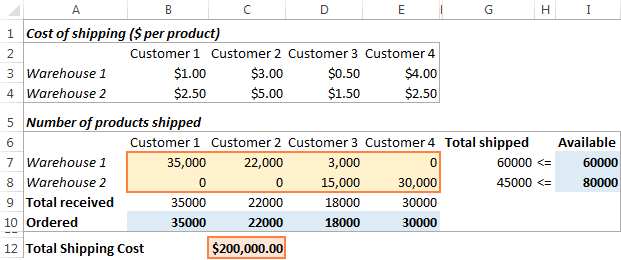
Sådan gemmer og indlæser du Excel Solver-scenarier
Når du løser en bestemt model, kan du gemme din Variabel celleværdier som et scenario, som du kan se eller genbruge senere.
Når du f.eks. beregner de minimale serviceomkostninger i det allerførste eksempel i denne vejledning, kan du prøve forskellige antal forventede kunder pr. måned og se, hvordan det påvirker serviceomkostningerne. Du kan gemme det mest sandsynlige scenario, du allerede har beregnet, og gendanne det når som helst.
Gemmer et Excel Solver-scenarie går ud på at vælge et område af celler, som dataene skal gemmes i. Indlæsning en Solver-model er blot et spørgsmål om at give Excel det område af celler, hvor din model er gemt. De detaljerede trin følger nedenfor.
Lagring af modellen
For at gemme Excel Solver-scenariet skal du udføre følgende trin:
- Åbn regnearket med den beregnede model, og kør Excel Solver.
- I den Parametre for opløseren vindue, skal du klikke på Indlæsning/opbevaring knap.
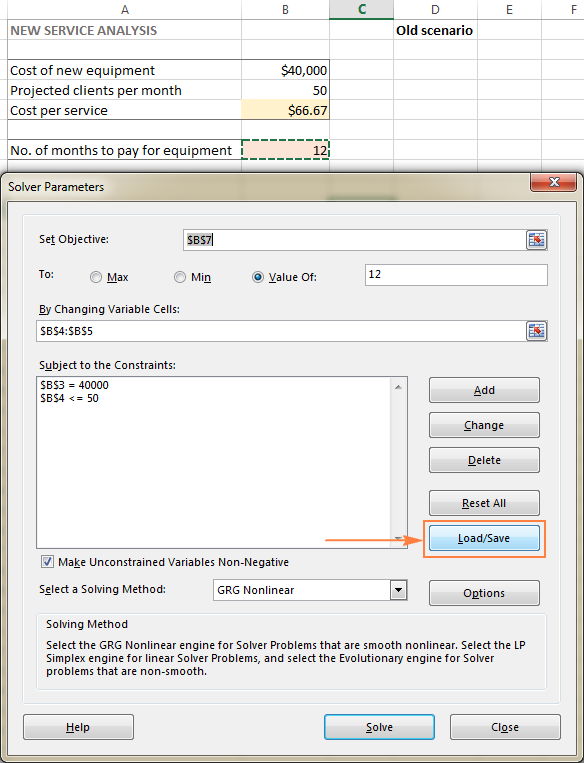
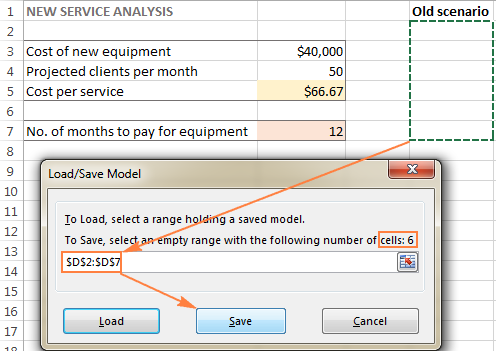
Samtidig har den Parametre for opløseren vises et vindue, hvor du kan ændre dine begrænsninger og prøve forskellige "hvad nu hvis"-muligheder.
Indlæsning af den gemte model
Når du beslutter dig for at gendanne det gemte scenarie, skal du gøre følgende:
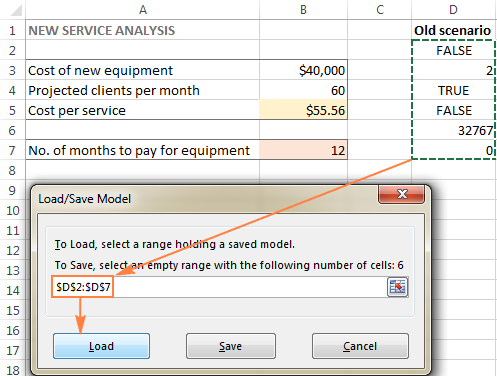
- I den Parametre for opløseren vindue, skal du klikke på Indlæsning/opbevaring knap.
- Vælg det område af celler, der indeholder den gemte model, på regnearket, og klik på Belastning :
Excel Solver-algoritmer
Når du definerer et problem til Excel Solver, kan du vælge en af følgende metoder i Vælg en løsningsmetode dropdown-boks:
- GRG Nonlinear. Generaliseret reduceret gradient Ikke-lineær algoritmen anvendes til problemer, der er glatte ikke-lineære, dvs. hvor mindst en af begrænsningerne er en glat ikke-lineær funktion af beslutningsvariablerne. Du kan finde flere oplysninger her.
- LP Simplex Simplex LP-løsningsmetoden er baseret på Simplex-algoritmen, der er skabt af den amerikanske matematiske videnskabsmand George Dantzig. Den bruges til at løse såkaldte Lineær programmering problemer - matematiske modeller, hvis krav er karakteriseret ved lineære sammenhænge, dvs. består af et enkelt mål repræsenteret ved en lineær ligning, som skal maksimeres eller minimeres. For yderligere oplysninger, se venligst denne side.
- Evolutionær Det bruges til ikke-godt-problemer, som er den vanskeligste type optimeringsproblemer at løse, fordi nogle af funktionerne er ikke-godt eller endog diskontinuerlige, og det er derfor svært at bestemme, i hvilken retning en funktion er stigende eller faldende. Du kan finde flere oplysninger på denne side.
Hvis du vil ændre, hvordan Solver finder en løsning, skal du klikke på Indstillinger knappen i Parametre for opløseren dialogboksen, og konfigurere alle indstillingerne i dialogboksen GRG Ikke-lineær , Alle metoder , og Evolutionær faner.
Sådan kan du bruge Solver i Excel til at finde de bedste løsninger på dine beslutningsproblemer. Og nu kan du downloade Excel Solver-eksemplerne, der er beskrevet i denne vejledning, og lave reverse-engineering af dem for at få en bedre forståelse. Jeg takker for din læsning og håber at se dig på vores blog i næste uge.

