Satura rādītājs
Šajā pamācībā ir izskaidrots, kā pievienot un kur atrast Solver dažādās Excel versijās, sākot no 2016 līdz 2003. Soli pa solim piemēros parādīts, kā izmantot Excel Solver, lai atrastu optimālus risinājumus lineārās programmēšanas un cita veida problēmām.
Ikviens zina, ka programmā Microsoft Excel ir daudz noderīgu funkciju un jaudīgu rīku, kas var ietaupīt stundām ilgu aprēķinu veikšanu. Bet vai zinājāt, ka tajā ir arī rīks, kas var palīdzēt jums atrast optimālus risinājumus lēmumu pieņemšanas problēmām?
Šajā pamācībā mēs aplūkosim visus būtiskākos Excel Solver papildinājuma aspektus un soli pa solim sniegsim norādījumus, kā to izmantot visefektīvāk.
Kas ir Excel Solver?
Excel risinātājs pieder īpašam komandu kopumam, ko bieži dēvē par What-if Analysis Tools. Tas galvenokārt paredzēts dažādu biznesa un inženiertehnisko modeļu simulācijai un optimizācijai.
Papildinājums Excel Solver ir īpaši noderīgs lineārās programmēšanas jeb lineārās optimizācijas problēmu risināšanai, tāpēc to dažkārt sauc par lineārās optimizācijas problēmu risināšanas lineārās programmēšanas risinātājs . Papildus tam tas var risināt gludas nelineāras un nelineāras problēmas. Lai iegūtu sīkāku informāciju, skatiet Excel Solver algoritmus.
Lai gan Solver nespēj atrisināt visas iespējamās problēmas, tas ir ļoti noderīgs, risinot visdažādākās optimizācijas problēmas, kad jums ir jāpieņem vislabākais lēmums. Piemēram, tas var palīdzēt maksimizēt ieguldījumu atdevi, izvēlēties optimālo budžetu reklāmas kampaņai, izveidot vislabāko darba grafiku darbiniekiem, samazināt piegādes izmaksas u. c.
Kā pievienot programmā Excel risinātāju
Risinātāja pievienojumprogramma ir iekļauta visās Microsoft Excel versijās, sākot ar 2003. gada versiju, taču pēc noklusējuma tā nav iespējota.
Lai pievienotu programmu Solver programmā Excel, veiciet šādas darbības:
- Programmā Excel 2010 - Excel 365 noklikšķiniet uz Faili > Iespējas .
Programmā Excel 2007 noklikšķiniet uz Microsoft Office pogu un pēc tam noklikšķiniet uz Excel opcijas .
- In the Excel opcijas dialoglodziņā noklikšķiniet uz Papildinājumi kreisajā sānjoslā, pārliecinieties, ka Excel papildinājumi ir atlasīts Pārvaldiet lodziņu loga apakšā un noklikšķiniet uz Go .
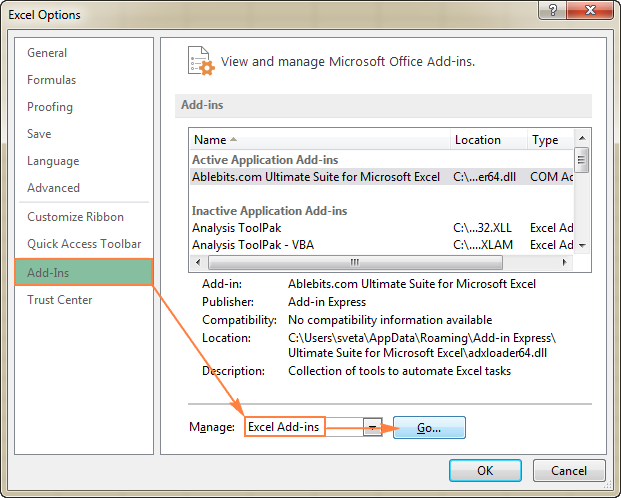
- In the Papildinājumi dialoglodziņā atzīmējiet Risinātāja papildinājums un noklikšķiniet uz LABI :
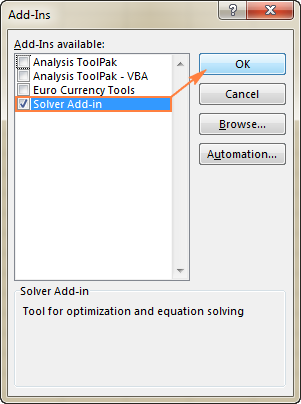
Risinātāja ieslēgšana Excel 2003 , dodieties uz Instrumenti izvēlni un noklikšķiniet uz Papildinājumi . In Papildinājumi pieejams sarakstu, pārbaudiet Risinātāja papildinājums un noklikšķiniet uz LABI .
Piezīme. Ja programmā Excel tiek parādīts ziņojums, ka jūsu datorā pašlaik nav instalēta papildprogramma Solver Add-in, noklikšķiniet uz . Jā lai to instalētu.
Kur programmā Excel ir risinātājs?
Mūsdienu Excel versijās Risinātājs tiek parādīta poga Dati cilnē Analīze grupa:

Kur programmā Excel 2003 ir risinātājs?
Pēc tam, kad programmā Excel 2003 ir ielādēts papildinājums Solver, tā komanda tiek pievienota programmai Instrumenti ēdienkarte:
Tagad, kad zināt, kur Excel programmā atrast Solver, atveriet jaunu darblapu un sāksim darbu!
Piezīme. Šajā pamācībā aplūkotajos piemēros ir izmantota Excel 2013 versija Solver. Ja jums ir cita Excel versija, ekrānšāviņi var neatbilst tieši jūsu versijai, lai gan Solver funkcionalitāte būtībā ir tāda pati.
Kā lietot solveri programmā Excel
Pirms palaist Excel Solver papildinājumu, formulējiet modeli, kuru vēlaties atrisināt darblapā. Šajā piemērā atradīsim risinājumu šādai vienkāršai optimizācijas problēmai.
Problēma Pieņemsim, ka esat skaistumkopšanas salona īpašnieks un plānojat saviem klientiem sniegt jaunu pakalpojumu. Šim nolūkam jums ir jāiegādājas jauna iekārta, kas maksā 40 000 ASV dolāru un kas ir jāsamaksā pa daļām 12 mēnešu laikā.
Mērķis : Aprēķiniet minimālās izmaksas par pakalpojumu, kas ļaus jums samaksāt par jauno aprīkojumu noteiktajā termiņā.
Šim uzdevumam esmu izveidojis šādu modeli:
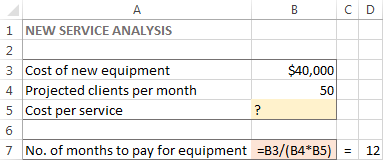
Un tagad aplūkosim, kā Excel Solver var atrast šīs problēmas risinājumu.
1. Palaist Excel risinātāju
Par Dati cilnē Analīze grupa, noklikšķiniet uz Risinātājs pogu.
2. Definēt problēmu
Portāls Risinātāja parametri tiks atvērts logs, kurā jāiestata 3 galvenie komponenti:
- Mērķa šūna
- Mainīgās šūnas
- Ierobežojumi
Ko tieši Excel Solver dara ar iepriekš minētajiem parametriem? Tas atrod optimālo vērtību (maksimālo, minimālo vai norādīto) formulai, kas atrodas tabulā Mērķis šūnā, mainot vērtības Mainīgs šūnām un ievērojot ierobežojumus, kas noteikti Ierobežojumi šūnas.
Mērķis
Portāls Mērķis šūna ( Mērķis šūna agrākajās Excel versijās) ir šūna kurā ir formula Mērķis var būt maksimizēt, minimizēt vai sasniegt kādu mērķa vērtību.
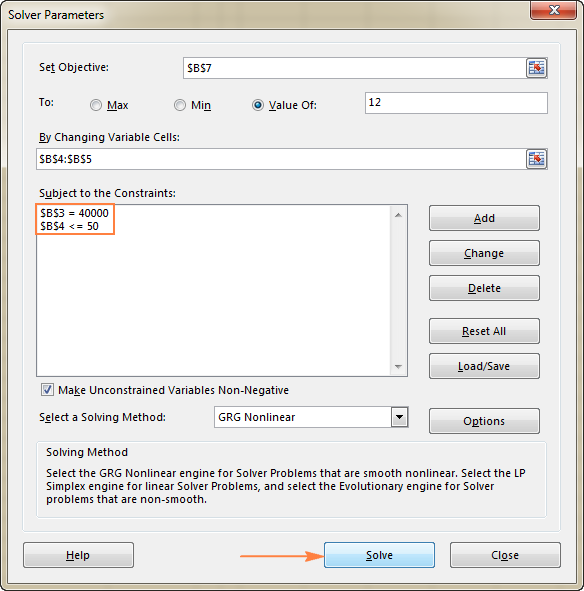
Šajā piemērā mērķa šūna ir B7, kas aprēķina maksājuma termiņu, izmantojot formulu =B3/(B4*B5) un formulas rezultātam jābūt vienādam ar 12:
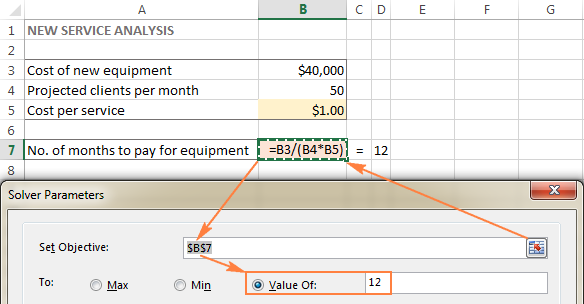
Mainīgās šūnas
Mainīgs šūnas ( Mainot šūnas vai Regulējams šūnas iepriekšējās versijās) ir šūnas, kurās ir mainīgie dati, kurus var mainīt, lai sasniegtu mērķi. Excel Solver ļauj norādīt līdz 200 mainīgo šūnu.
Šajā piemērā ir dažas šūnas, kuru vērtības var mainīt:
- Plānotie klienti mēnesī (B4), kuriem jābūt mazākiem vai vienādiem ar 50; un
- Izmaksas par pakalpojumu (B5), ko vēlamies, lai Excel Solver aprēķina.
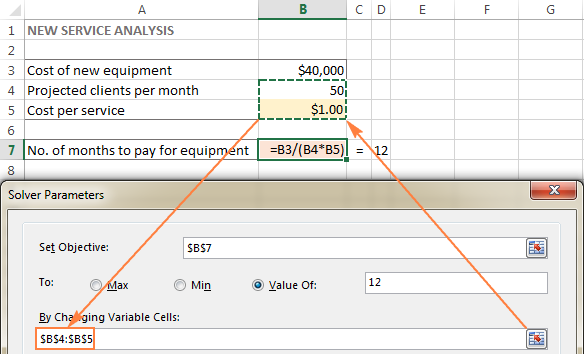
Padoms. Ja mainīgie elementi vai diapazoni jūsu modelī ir nesaderīgs , atlasiet pirmo šūnu vai diapazonu un pēc tam, atlasot citas šūnas un/vai diapazonus, nospiediet un turiet taustiņu Ctrl. Vai arī manuāli ievadiet diapazonus, atdalot tos ar komatiem.
Ierobežojumi
Excel risinātājs Ierobežojumi ierobežojumi ir problēmas iespējamo risinājumu ierobežojumi vai robežas. Citādi sakot, ierobežojumi ir nosacījumi, kas jāievēro.
Lai pievienotu ierobežojumu(-us), veiciet šādas darbības:
- Noklikšķiniet uz Pievienot pogu pa labi uz " Ievērojot ierobežojumus " lodziņš.
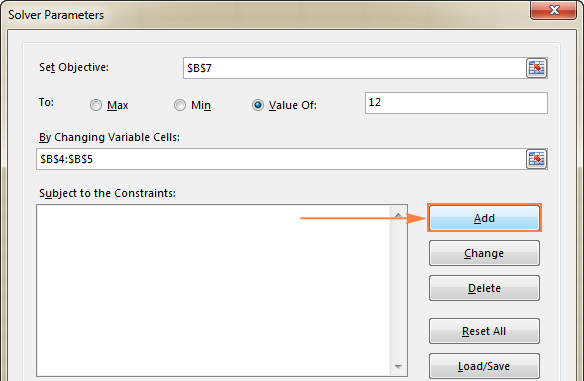
- In the Ierobežojums logā ievadiet ierobežojumu.
- Noklikšķiniet uz Pievienot lai pievienotu ierobežojumu sarakstam.
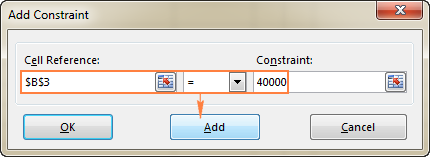
- Turpiniet ievadīt citus ierobežojumus.
- Pēc tam, kad esat ievadījis pēdējo ierobežojumu, noklikšķiniet uz LABI lai atgrieztos galvenajā Risinātājs Parametri logs.
Excel Solver ļauj norādīt šādas attiecības starp atsaukto šūnu un ierobežojumu.
- Mazāk par vai vienāds ar , vienāds ar , un lielāks vai vienāds ar . Šīs attiecības iestatāt, atlasot šūnas logā. Atsauce uz šūnām lodziņu, izvēloties vienu no šādām zīmēm: <= , =, vai >= un pēc tam ierakstot skaitli, šūnas atsauci / šūnas nosaukumu vai formulu. Ierobežojums lodziņā (skatiet iepriekš redzamo ekrāna attēlu).
- Vesels skaitlis . Ja atsaucē norādītajai šūnai jābūt veselam skaitlim, atlasiet int , un vārds vesels skaitlis parādīsies Ierobežojums kaste.
- Dažādas vērtības Ja katrā šūnā atsauces diapazonā jānorāda atšķirīga vērtība, atlasiet dif , un vārds AllDifferent parādīsies Ierobežojums kaste.
- Binary Ja vēlaties ierobežot atsauci uz šūnu līdz 0 vai 1, atlasiet bin , un vārds binary parādīsies Ierobežojums kaste.
Piezīme. int , bin , un dif attiecības var izmantot tikai mainīgo šūnu ierobežojumiem.
Uz rediģēt vai dzēst esošo ierobežojumu, veiciet šādus darbības:
- In the Risinātāja parametri dialoglodziņā noklikšķiniet uz ierobežojuma.
- Lai mainītu atlasīto ierobežojumu, noklikšķiniet uz Mainīt un veiciet vēlamās izmaiņas.
- Lai dzēstu ierobežojumu, noklikšķiniet uz Dzēst pogu.
Šajā piemērā ierobežojumi ir šādi:
- B3=40000 - jaunā aprīkojuma izmaksas ir $40 000.
- B4<=50 - prognozēto pacientu skaits mēnesī zem 50.
3. Atrisiniet problēmu
Kad esat konfigurējis visus parametrus, noklikšķiniet uz pogas Atrisināt pogu apakšā Risinātāja parametri logu (skat. ekrānattēlu iepriekš) un ļaujiet Excel Solver papildinājumam atrast optimālo problēmas risinājumu.
Atkarībā no modeļa sarežģītības, datora atmiņas un procesora ātruma tas var aizņemt dažas sekundes, dažas minūtes vai pat dažas stundas.
Kad Solver ir pabeidzis apstrādi, tas parādīs Risinātāja rezultāti dialoglodziņu, kurā atlasiet Risinātāja risinājuma saglabāšana un noklikšķiniet uz LABI :
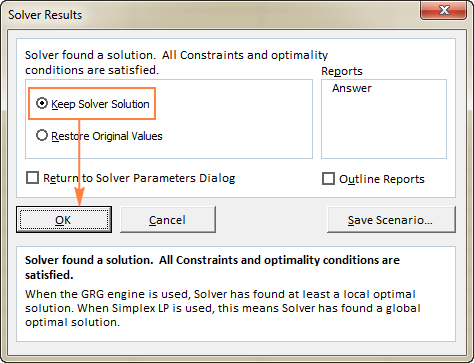
Portāls Risinātāja rezultāts logs tiks aizvērts, un risinājums uzreiz parādīsies darblapā.
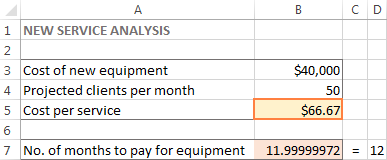
Šajā piemērā B5 ailē parādās 66,67 $, kas ir minimālās izmaksas par pakalpojumu, kas ļaus jums samaksāt par jauno aprīkojumu 12 mēnešu laikā, ja mēnesī ir vismaz 50 klientu:
Padomi:
- Ja Excel Solver pārāk ilgi apstrādā noteiktu problēmu, varat pārtraukt procesu, nospiežot taustiņu Esc. Excel pārrēķinās darblapu ar pēdējām atrastajām vērtībām, lai atrisinātu problēmu. Mainīgs šūnas.
- Lai iegūtu sīkāku informāciju par atrisināto problēmu, noklikšķiniet uz ziņojuma tipa sadaļā Ziņojumi un pēc tam noklikšķiniet uz LABI . Pārskats tiks izveidots jaunā darblapā:
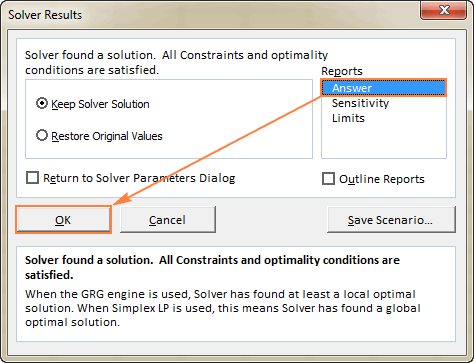
Tagad, kad esat guvuši priekšstatu par to, kā Excel programmā izmantot Solver, aplūkosim vēl dažus piemērus, kas varētu jums palīdzēt labāk izprast šo funkciju.
Excel Solver piemēri
Tālāk atradīsiet vēl divus Excel Solver papildinājuma lietošanas piemērus. Vispirms mēs atradīsim risinājumu kādai labi zināmai mīklai un pēc tam atrisināsim reālu lineārās programmēšanas problēmu.
Excel Solver 1. piemērs (burvju kvadrāts)
Domāju, ka ikviens ir iepazinies ar "burvju kvadrāta" mīklām, kurās kvadrātā ir jāsaliek skaitļu kopums tā, lai visas rindas, stabiņi un diagonāles sakrājas līdz noteiktam skaitlim.
Piemēram, vai jūs zināt risinājumu 3x3 kvadrātam ar skaitļiem no 1 līdz 9, kur katra rinda, sleja un diagonāle ir 15?
Iespējams, nav nekas liels, ja šo mīklu atrisināsim ar mēģinājumu un kļūdu palīdzību, bet es deru derēt, ka Solver atradīs risinājumu ātrāk. Mūsu darba daļa ir pareizi definēt problēmu.
Sākumā tabulā, kas sastāv no 3 rindām un 3 kolonnām, ievadiet skaitļus no 1 līdz 9. Excel Solver faktiski nav nepieciešami šie skaitļi, bet tie palīdzēs mums vizualizēt problēmu. Excel Solver papildinājumam patiešām ir nepieciešamas SUM formulas, kas summē katru rindu, kolonnu un 2 diagonāles:
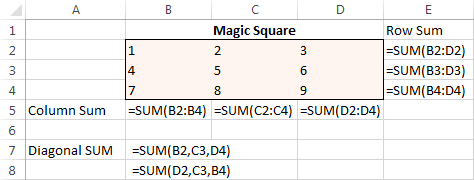
Kad visas formulas ir ieviestas, palaidiet Solver un iestatiet šādus parametrus:
- Komplekts Mērķis . Šajā piemērā mums nav nepieciešams iestatīt mērķi, tāpēc atstājiet šo lodziņu tukšu.
- Mainīgās šūnas Mēs vēlamies aizpildīt šūnas B2 līdz D4, tāpēc atlasiet diapazonu B2:D4.
- Ierobežojumi Jāievēro šādi nosacījumi:
- $B$2:$D$4 = AllDifferent - visās mainīgo šūnās jābūt dažādām vērtībām.
- $B$2:$D$4 = vesels skaitlis - visām mainīgo vienībām jābūt veseliem skaitļiem.
- $B$5:$D$5 = 15 - vērtību summai katrā slejā jābūt vienādai ar 15.
- $E$2:$E$4 = 15 - vērtību summai katrā rindā jābūt vienādai ar 15.
- $B$7:$B$8 = 15 - abu diagonāļu summai jābūt vienādai ar 15.
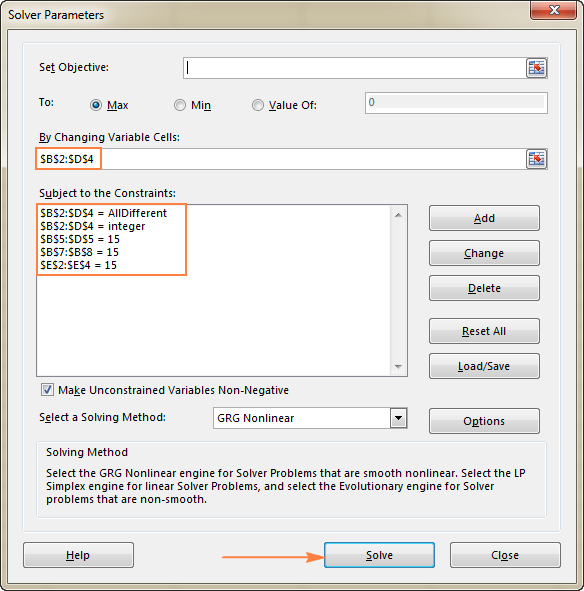
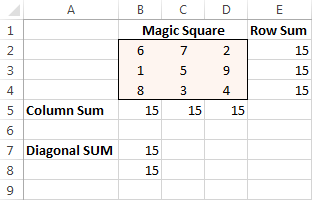
Visbeidzot noklikšķiniet uz Atrisināt pogu, un risinājums ir pieejams!
Excel Solver 2. piemērs (lineārās programmēšanas problēma)
Šis ir vienkāršas transporta optimizācijas problēmas piemērs ar lineāru mērķi. Daudzos uzņēmumos tiek izmantoti sarežģītāki šāda veida optimizācijas modeļi, lai katru gadu ietaupītu tūkstošiem dolāru.
Problēma : Jūs vēlaties minimizēt izmaksas preču nosūtīšanai no 2 dažādām noliktavām 4 dažādiem klientiem. Katrā noliktavā ir ierobežots piedāvājums, un katram klientam ir noteikts pieprasījums.
Mērķis : Minimizēt kopējās piegādes izmaksas, nepārsniedzot katrā noliktavā pieejamo daudzumu un apmierinot katra klienta pieprasījumu.
Avota dati
Lūk, kā izskatās mūsu transporta optimizācijas problēma:
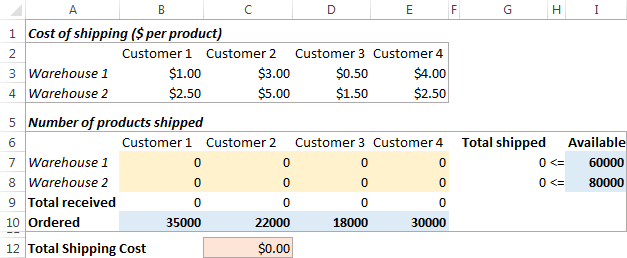
Modeļa formulēšana
Lai definētu mūsu lineārās programmēšanas problēmu Excel risinātājam, atbildēsim uz 3 galvenajiem jautājumiem:
- Kādi lēmumi ir jāpieņem? Mēs vēlamies aprēķināt optimālo preču daudzumu, ko piegādāt katram klientam no katras noliktavas. Tie ir šādi. Mainīgs šūnas (B7:E8).
- Kādi ir ierobežojumi? Katrā noliktavā pieejamie krājumi (I7:I8) nedrīkst pārsniegt pieejamo krājumu apjomu, un ir jāpiegādā katra klienta pasūtītais daudzums (B10:E10). Tie ir šādi. Ierobežots šūnas.
- Kāds ir mērķis? Minimālas kopējās izmaksas par piegādi. Un tas ir mūsu Mērķis šūna (C12).
Nākamais, kas jums jāizdara, ir jāaprēķina kopējais daudzums, kas nosūtīts no katras noliktavas (G7:G8), un kopējais preču daudzums, ko saņēmis katrs klients (B9:E9). To var izdarīt, izmantojot vienkāršas summēšanas formulas, kas parādītas tālāk redzamajā ekrānšāviņā. Lai aprēķinātu kopējās piegādes izmaksas, C12 laukā ievietojiet arī formulu SUMPRODUCT:
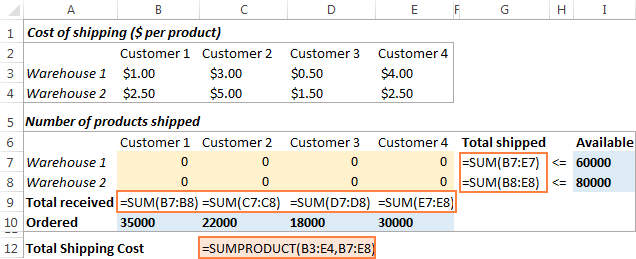
Lai padarītu mūsu transporta optimizācijas modeli vieglāk saprotamu, izveidojiet šādus nosauktus diapazonus:
| Diapazona nosaukums | Šūnas | Risinātāja parametrs |
| Produkti_nosūtīti | B7:E8 | Mainīgās šūnas |
| Pieejams | I7:I8 | Ierobežojums |
| Kopā_nosūtīts | G7: G8 | Ierobežojums |
| Pasūtīts | B10:E10 | Ierobežojums |
| Kopā_saņemts | B9:E9 | Ierobežojums |
| Shipping_cost | C12 | Mērķis |
Pēdējā lieta, kas jums vēl ir jāizdara, ir jākonfigurē Excel Solver parametri:
- Mērķis: Shipping_cost iestatīts uz Min
- Mainīgās šūnas: Products_shipped
- Ierobežojumi: Kopā_saņemts = Pasūtīts un Kopā_nosūtīts <= Pieejams.
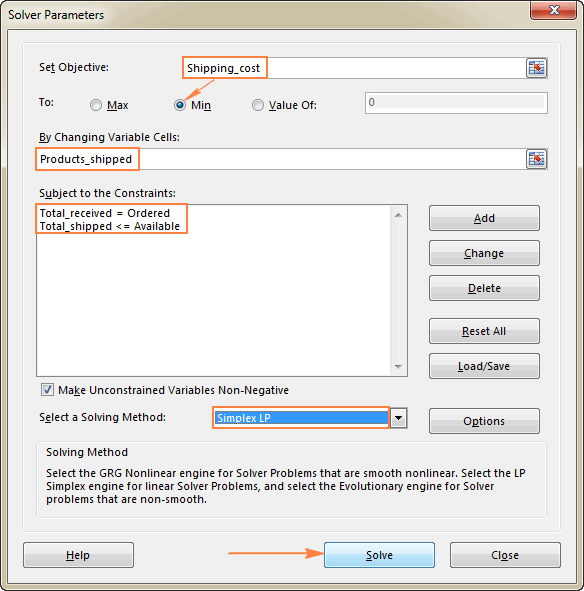
Lūdzu, pievērsiet uzmanību, ka esam izvēlējušies Simplex LP risināšanas metodi šajā piemērā, jo mēs strādājam ar lineārās programmēšanas problēmu. Ja neesat pārliecināts, kāda veida problēma ir jūsu problēma, varat atstāt noklusējuma iestatījumu. GRG nelineārais Sīkāku informāciju skatiet sadaļā Excel Solver algoritmi.
Risinājums
Noklikšķiniet uz Atrisināt pogu apakšā Risinātāja parametri Šajā piemērā Excel Solver papildinājums aprēķināja optimālo preču daudzumu, ko piegādāt katram klientam no katras noliktavas ar minimālām kopējām piegādes izmaksām:
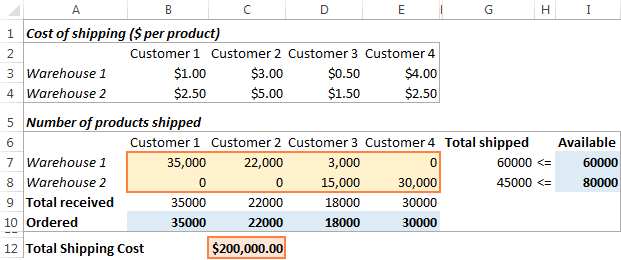
Kā saglabāt un ielādēt Excel Solver scenārijus
Risinot konkrētu modeli, iespējams, vēlēsieties saglabāt savu Mainīgs šūnu vērtības kā scenāriju, ko vēlāk varat skatīt vai atkārtoti izmantot.
Piemēram, aprēķinot minimālās pakalpojuma izmaksas pašā pirmajā šajā pamācībā aplūkotajā piemērā, iespējams, vēlēsieties izmēģināt dažādus prognozējamo klientu skaitu mēnesī un redzēt, kā tas ietekmē pakalpojuma izmaksas. Tajā pašā laikā varat saglabāt jau aprēķināto visticamāko scenāriju un jebkurā brīdī to atjaunot.
Glābšana Excel Solver scenārijā ir jāizvēlas šūnu diapazons, kurā saglabāt datus. Iekraušana Solver modelis ir tikai jānorāda Excel šūnu diapazons, kurā ir saglabāts modelis. Tālāk ir aprakstīti detalizēti soļi.
Modeļa saglabāšana
Lai saglabātu Excel Solver scenāriju, veiciet šādas darbības:
- Atveriet darblapu ar aprēķināto modeli un palaidiet Excel Solver.
- In the Risinātāja parametri logā noklikšķiniet uz Ielādēt/izglabāt pogu.
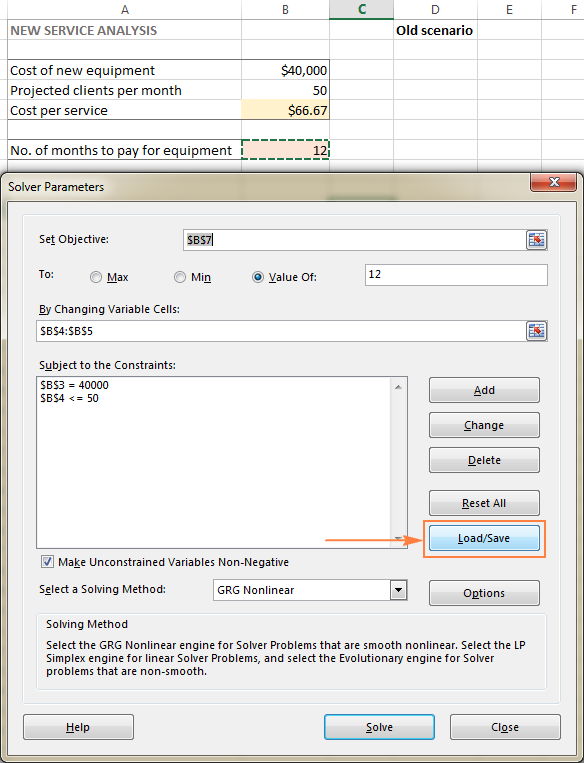
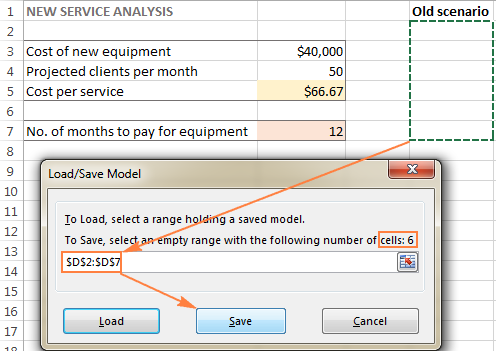
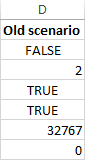
Tajā pašā laikā Risinātāja parametri tiks parādīts logs, kurā varat mainīt ierobežojumus un izmēģināt dažādas "kas, ja" iespējas.
Saglabātā modeļa ielādēšana
Kad esat nolēmis atjaunot saglabāto scenāriju, veiciet šādas darbības:
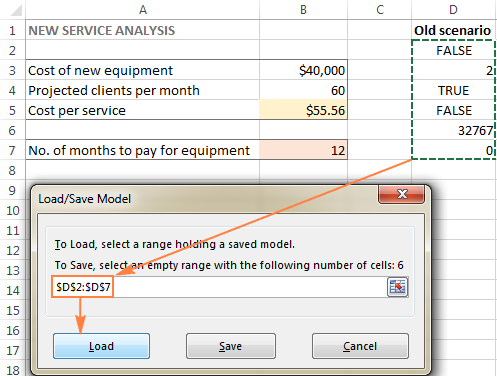
- In the Risinātāja parametri logā noklikšķiniet uz Ielādēt/izglabāt pogu.
- Darba lapā atlasiet šūnu diapazonu, kurā ir saglabāts modelis, un noklikšķiniet uz Ielādēt :
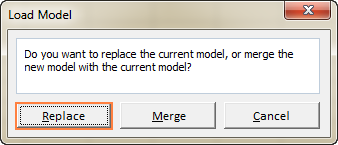
Excel Solver algoritmi
Definējot problēmu Excel risinātājam, varat izvēlēties vienu no šādām metodēm. Izvēlieties risināšanas metodi nolaižamajā lodziņā:
- GRG Nonlinear. Vispārināts reducētā gradienta nelineārais algoritmu izmanto problēmām, kas ir gludas nelineāras, t. i., kurās vismaz viens no ierobežojumiem ir gluda nelineāra lēmuma mainīgo funkcija. Sīkāku informāciju var atrast šeit.
- LP Simplex Simplex LP risināšanas metodes pamatā ir amerikāņu matemātiķa Džordža Danciga (George Dantzig) radītais Simplex algoritms, ko izmanto, lai risinātu t. s. "vienkārx" algoritmu. Lineārā programmēšana uzdevumi - matemātiski modeļi, kuru prasības raksturo lineāras sakarības, t. i., tie sastāv no viena mērķa, kas izteikts ar lineāru vienādojumu, kurš ir maksimizējams vai minimizējams. Lai iegūtu vairāk informācijas, lūdzu, skatiet šo lapu.
- Evolūcijas . To izmanto nelīdzenu problēmu risināšanai, kas ir visgrūtāk risināmā optimizācijas problēmu veida problēmas, jo dažas funkcijas ir nelīdzenas vai pat pārtrauktas, un tāpēc ir grūti noteikt, kurā virzienā funkcija pieaug vai samazinās. Lai iegūtu vairāk informācijas, skatiet šo lapu.
Lai mainītu veidu, kā Solver atrod risinājumu, noklikšķiniet uz Iespējas pogu Risinātāja parametri dialoglodziņu un konfigurējiet jebkuru vai visas opcijas, kas attiecas uz GRG nelineārais , Visas metodes , un Evolūcijas cilnes.
Tā jūs varat izmantot Solver Excel programmā, lai atrastu labākos risinājumus savām lēmumu pieņemšanas problēmām. Un tagad jūs varat lejupielādēt šajā pamācībā aplūkotos Excel Solver piemērus un apgriezt tos, lai labāk izprastu. Paldies, ka izlasījāt, un ceru, ka nākamnedēļ tiksimies mūsu emuārā.

