Преглед садржаја
Водич објашњава како да додате и где да пронађете Солвер у различитим верзијама Екцел-а, од 2016. до 2003. Примери корак по корак показују како да користите Екцел Солвер за проналажење оптималних решења за линеарно програмирање и друге врсте проблема.
Сви знају да Мицрософт Екцел садржи много корисних функција и моћних алата који вам могу уштедети сате прорачуна. Али да ли сте знали да има и алат који вам може помоћи да пронађете оптимална решења за проблеме одлучивања?
У овом водичу ћемо покрити све суштинске аспекте додатка Екцел Солвер и пружити корак водич по корак о томе како да га најефикасније користите.
Шта је Екцел Солвер?
Екцел Солвер припада посебном скупу команде које се често називају алаткама за анализу шта ако. Првенствено је намењен за симулацију и оптимизацију различитих пословних и инжењерских модела.
Додатак Екцел Солвер је посебно користан за решавање проблема линеарног програмирања, познатих као проблеми линеарне оптимизације, и стога се понекад назива решавач линеарног програмирања . Осим тога, може да реши глатке нелинеарне и не-глатке проблеме. За више детаља погледајте алгоритме Екцел Солвер-а.
Иако Решавач не може да реши сваки могући проблем, заиста је од помоћи када се бавите свим врстама проблема оптимизације где треба да донесете најбољу одлуку. На пример, можеколичина коју наручи сваки купац (Б10:Е10) треба да буде испоручена. Ово су Ограничене ћелије .
Следећа ствар коју треба да урадите је да израчунате укупну количину испоручену из сваког складишта (Г7:Г8), и укупна роба коју је примио сваки купац (Б9:Е9). То можете учинити помоћу једноставних формула за збир приказаних на слици испод. Такође, уметните формулу СУМПРОДУЦТ у Ц12 да бисте израчунали укупне трошкове испоруке:
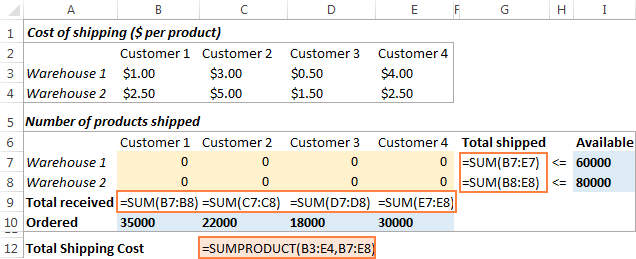
Да би наш модел оптимизације транспорта био лакши за разумевање, креирајте следеће именоване опсеге:
| Назив опсега | Ћелије | Параметар решавача |
| Производи_испоручени | Б7: Е8 | Променљиве ћелије |
| Доступне | И7:И8 | Ограничење |
| Тотал_схиппед | Г7:Г8 | Ограничење |
| Наручено | Б10:Е10 | Ограничење |
| Укупно_примљено | Б9:Е9 | Ограничење |
| Схиппинг_цост | Ц12 | Циљ |
Последња ствар коју треба да урадите је да конфигуришете параметре Екцел Солвера:
- Циљ: Трошкови испоруке постављени на Мин
- Променљиве ћелије: Продуцтс_схиппед
- Ограничења: Тотал_рецеивед = Ордеред и Тотал_схиппед &лт;= Доступно
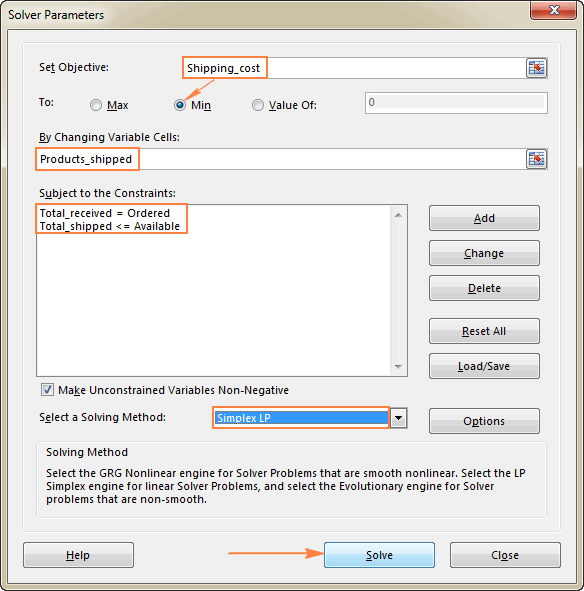
Молимо платите пажња коју смо изабрали Симплек ЛП метод решавања у овом примеру јер се бавимо проблемом линеарног програмирања. Ако нисте сигурни која је врста вашег проблема, можете оставити подразумевани ГРГ нелинеарни метод решавања. За више информација погледајте Алгоритме Екцел Солвера.
Решење
Кликните на дугме Реши на дну прозора Параметри решавача и добиће ваш одговор. У овом примеру, додатак Екцел Солвер израчунао је оптималну количину робе за испоруку сваком купцу из сваког складишта уз минималне укупне трошкове испоруке:
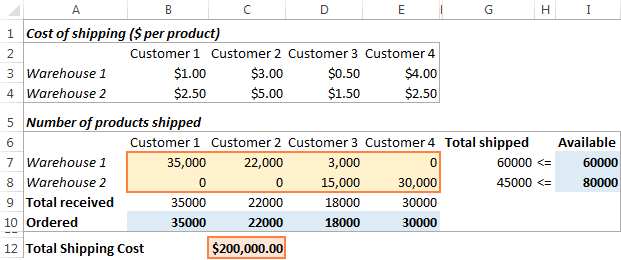
Како уштедети и учитајте сценарије Екцел Солвер
Када решавате одређени модел, можда ћете желети да сачувате вредности ћелије Вариабле као сценарио који можете да погледате или поново користите касније.
На пример, када израчунавате минималну цену услуге у првом примеру о коме се говори у овом водичу, можда ћете желети да испробате различите бројеве пројектованих клијената месечно и видите како то утиче на цену услуге. При томе, можда ћете желети да сачувате највероватнији сценарио који сте већ израчунали и вратите га у било ком тренутку.
Чување Екцел Солвер сценарија се своди на избор опсега ћелија за сачувајте податке у. Учитавање Солвер модела је само питање пружања Екцел-у опсега ћелија у којима је ваш модел сачуван. Детаљни кораци следе у наставку.
Чувањемодел
Да бисте сачували сценарио Екцел Солвер, извршите следеће кораке:
- Отворите радни лист са израчунатим моделом и покрените Екцел Солвер.
- У Прозор Параметри решавача , кликните на дугме Учитај/Сачувај .
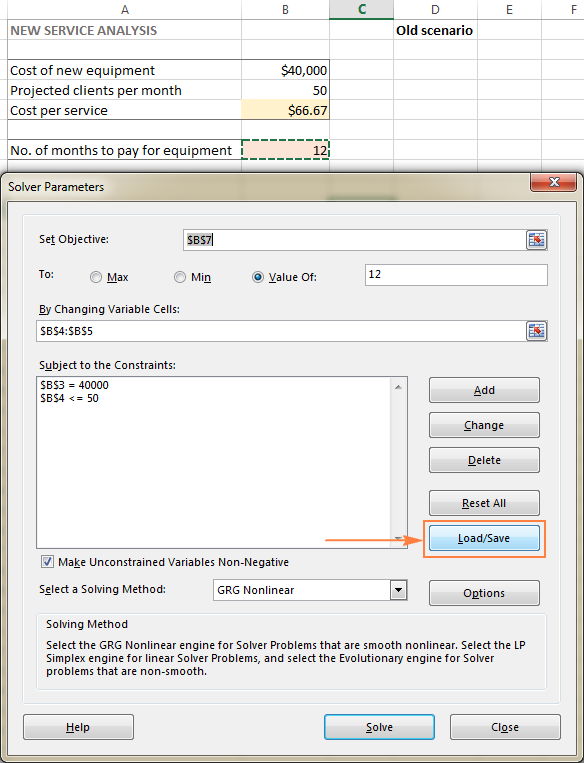
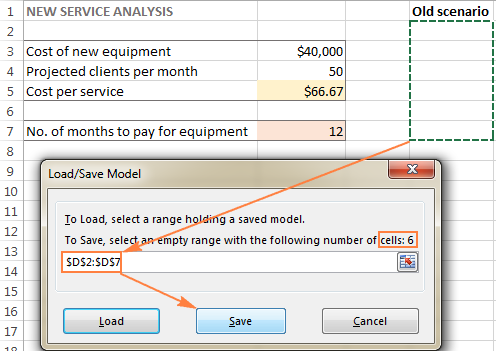
Истовремено ће се појавити прозор Параметри решавача где можете да промените своја ограничења и испробате различите опције „шта ако“.
Учитавање сачувани модел
Када одлучите да вратите сачувани сценарио, урадите следеће:
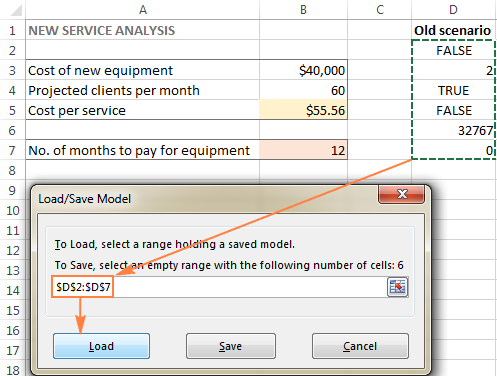
- У прозору Параметри решавача кликните на Учитај/ Дугме Сачувај .
- На радном листу изаберите опсег ћелија које држе сачувани модел и кликните на Учитај :
Алгоритми Екцел Солвера
Када дефинишете проблем за Екцел Решавач, можете да изаберете један од следећих метода у падајућем оквиру Изаберите метод решавања :
- ГРГ нелинеарни. Генерализовани редуковани нелинеарни градијент алгоритам се користи за проблеме који су глатки нелинеарни, тј. у којима је бар једно од ограничења глатка нелинеарна функција променљивих одлуке. Више детаља можете пронаћи овде.
- ЛП Симплек . Метода Симплек ЛП Солвинга заснива се на Симплек алгоритму који је креирао амерички математичар Џорџ Данциг. Користи се за решавање такозваних проблема Линеарног програмирања - математичких модела чије захтеве карактеришу линеарни односи, односно састоје се од једног циља представљеног линеарном једначином која мора бити максимизирана или минимизирана. За више информација, погледајте ову страницу.
- Еволуционарно . Користи се за неглатке проблеме, који су најтежи тип оптимизацијских проблема за решавање јер су неке од функција неглатке или чак дисконтинуалне, па је стога тешко одредити правац у коме се функција повећава или смањује. За више информација, погледајте ову страницу.
Да бисте променили начин на који Решавач проналази решење, кликните на дугме Опције у дијалогу Параметри решавача и конфигуришите било коју или све опције на картицама ГРГ Нелинеар , Сви методи и Еволуционарни .
Овако можете да користите Солвер у Екцел-у да пронађете најбоља решења за ваше проблеме одлучивања. А сада, можда желитепреузмите примере Екцел Солвер-а о којима се говори у овом водичу и извршите их обрнутим инжењерингом ради бољег разумевања. Захваљујем вам што сте читали и надам се да ћемо се следеће недеље видети на нашем блогу.
помаже вам да максимизирате повраћај улагања, изаберете оптимални буџет за вашу рекламну кампању, направите најбољи распоред рада за своје запослене, смањите трошкове испоруке и тако даље.Како додати Солвер у Екцел
Додатак Солвер је укључен у све верзије Мицрософт Екцел-а почевши од 2003. године, али није подразумевано омогућен.
Да бисте додали Солвер у свој Екцел, извршите следеће кораке:
- У програму Екцел 2010 – Екцел 365, кликните на Датотека &гт; Опције .
У програму Екцел 2007 кликните на дугме Мицрософт Оффице и затим кликните на Екцел опције .
- У дијалогу Екцел опције кликните на Додаци на левој бочној траци, уверите се да Екцел додаци је изабран у пољу Управљање на дну прозора и кликните на Иди .
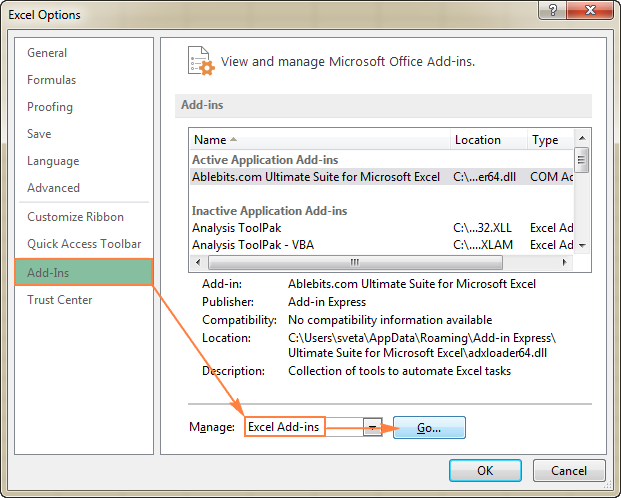
- У Додаци дијалог, означите поље Додатак за решавање и кликните на ОК :
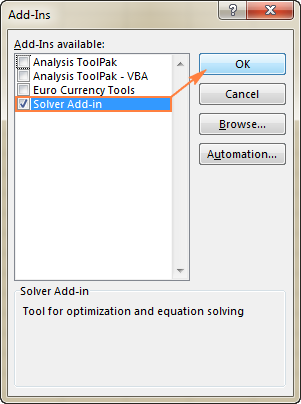
Да бисте добили Солвер на Екцел 2003 , идите на мени Алати и кликните на Додаци . На листи Додаци доступни , означите поље Додатак за решавање и кликните на ОК .
Белешка. Ако Екцел прикаже поруку да додатак Солвер тренутно није инсталиран на вашем рачунару, кликните на Да да бисте га инсталирали.
Где је Солвер у Екцел-у?
У модерним верзијама Екцел-а, дугме Решавач се појављује на картици Подаци , у Анализи група:

Где јеРешавач у програму Екцел 2003?
Након што се додатак Солвер учита у Екцел 2003, његова команда се додаје у мени Алатке :
Сада када знате где да пронађете Солвер у Екцел-у, отворите нови радни лист и почнимо!
Напомена. Примери о којима се говори у овом водичу користе Солвер у програму Екцел 2013. Ако имате другу верзију програма Екцел, снимци екрана се можда неће у потпуности подударати са вашом верзијом, иако је функционалност Решавача у основи иста.
Како користити Солвер у Екцел-у
Пре покретања додатка Екцел Солвер, формулишите модел који желите да решите у радном листу. У овом примеру, хајде да пронађемо решење за следећи једноставан проблем оптимизације.
Проблем . Претпоставимо да сте власник козметичког салона и планирате да својим клијентима пружите нову услугу. За ово морате да купите нову опрему која кошта 40.000 долара, коју треба платити на рате у року од 12 месеци.
Циљ : Израчунајте минималну цену по услузи која ће вам омогућити да платите нову опрему у наведеном временском оквиру.
За овај задатак, направио сам следећи модел:
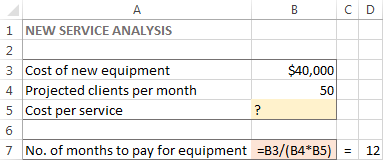
А сада, да видимо како Екцел Солвер може пронаћи решење за овај проблем.
1. Покрените Екцел Солвер
На картици Подаци , у групи Анализа кликните на дугме Решавач .
2. Дефинишите проблем
Прозор Параметри решавача ће се отворити тамо где иматеда бисте подесили 3 примарне компоненте:
- Целија циља
- Променљиве ћелије
- Ограничења
Тачно шта ради Екцел Солвер са горе наведене параметре? Проналази оптималну вредност (максимална, минимална или наведена) за формулу у ћелији Циљ тако што мења вредности у ћелијама Променљива и подлеже ограничењима у Ограничењима ћелије.
Циљ
Ћелија Циљ ( Циља ћелија у ранијим верзијама Екцел-а) је ћелија која садржи формулу који представља циљ или циљ проблема. Циљ може бити да се максимизира, минимизира или постигне нека циљна вредност.
У овом примеру, циљна ћелија је Б7, која израчунава рок плаћања користећи формулу =B3/(B4*B5) и резултат формуле треба да буде једнак 12:
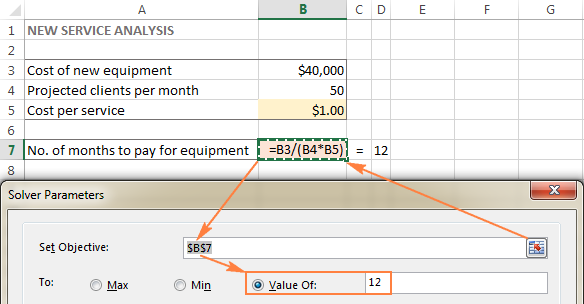
Променљиве ћелије
Променљиве ћелије ( Променљиве ћелије или Прилагодљиве ћелије у ранијим верзијама) су ћелије које садрже променљиве податке који се могу мењати да би се постигао циљ. Екцел Солвер омогућава навођење до 200 променљивих ћелија.
У овом примеру имамо неколико ћелија чије вредности могу да се мењају:
- Пројектовани клијенти месечно (Б4) који би требало бити мањи или једнак 50; и
- Цена по услузи (Б5) коју желимо да израчуна Екцел Солвер.
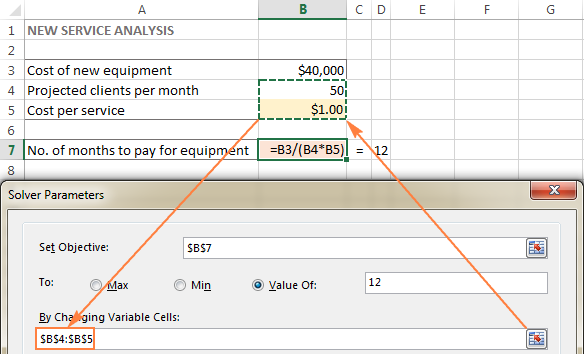
Савет. Ако су променљиве ћелије или опсези у вашем моделу несуседни ,изаберите прву ћелију или опсег, а затим притисните и држите тастер Цтрл док бирате друге ћелије и/или опсеге. Или унесите опсеге ручно, одвојене зарезима.
Ограничења
Екцел Солвер Ограничења су ограничења или ограничења могућих решења проблема. Другачије речено, ограничења су услови који морају бити испуњени.
Да бисте додали ограничење(а), урадите следеће:
- Кликните на Додај дугме десно до оквира „ Субјецт то тхе Цонстраинтс ”.
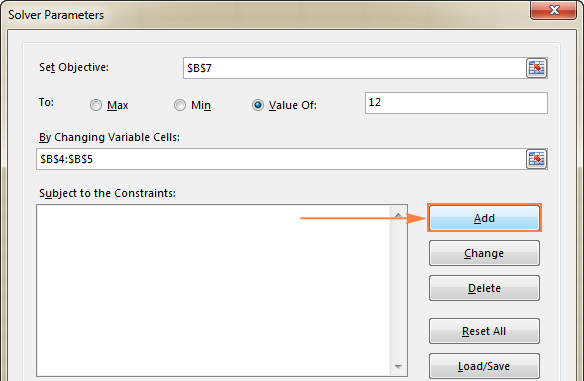
- У прозору Цонстраинт , унесите ограничење.
- Кликните на дугме Додај да бисте додали ограничење на листу.
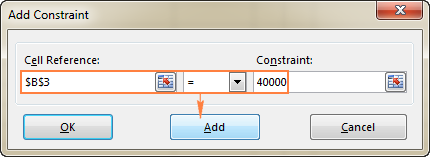
- Настави унос других ограничења.
- Након што сте унели коначно ограничење, кликните на ОК да бисте се вратили у главни прозор Решавач Параметерс .
Екцел Солвер омогућава навођење следећих односа између референтне ћелије и ограничења.
- Мање или једнако , једнако , и веће или једнако . Ове односе постављате тако што ћете изабрати ћелију у пољу Референца на ћелију , изабрати један од следећих знакова: &лт;= , =, или &гт ;= , а затим откуцајте број, референцу ћелије/име ћелије или формулу у поље Ограничење (погледајте горњи снимак екрана).
- Цео број . Ако референцирана ћелија мора бити цео број, изаберите инт ,и реч интегер ће се појавити у пољу Цонстраинт .
- Различите вредности . Ако свака ћелија у референтном опсегу мора да садржи другачију вредност, изаберите диф и реч АллДифферент ће се појавити у пољу Цонстраинт .
- Бинарни . Ако желите да ограничите референцирану ћелију на 0 или 1, изаберите бин , а реч бинари ће се појавити у пољу Цонстраинт .
Напомена. Релације инт , бин и диф могу се користити само за ограничења ћелија променљиве.
Да бисте изменили или избрисали постојеће ограничење урадите следеће:
- У дијалогу Параметри решавача кликните на ограничење.
- Да бисте изменили изабрано ограничење, кликните на Промени и унесите промене које желите.
- Да бисте избрисали ограничење, кликните на дугме Избриши .
У овом примеру, ограничења су:
- Б3=40000 – цена нове опреме је 40 000 УСД.
- Б4&лт;=50 – број пројектованих пацијената месечно испод 50.
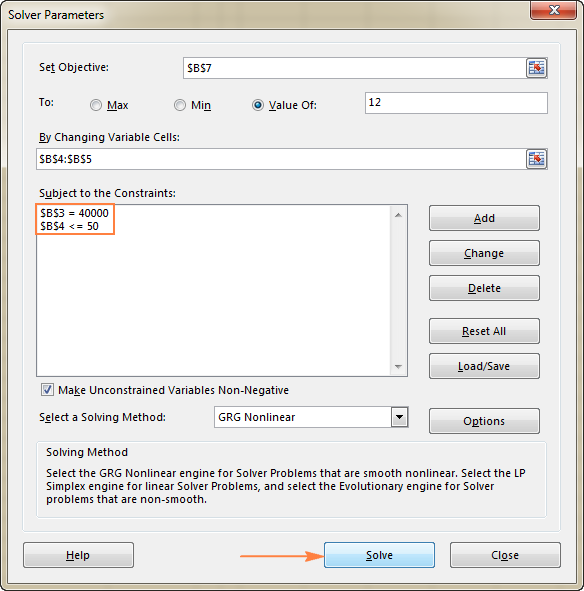
3. Реши проблем
Након што сте конфигурисали све параметре, кликните на дугме Реши на дну прозора Параметри решавача (погледајте снимак екрана изнад) и пустите додатак Екцел Солвер проналази оптимално решење за ваш проблем.
У зависности од сложености модела, рачунарске меморије и брзине процесора, може потрајати неколикосекунди, неколико минута или чак неколико сати.
Када Решавач заврши са обрадом, приказаће прозор за дијалог Резултати решавања , где бирате Задржи решење решавача и кликните на ОК :
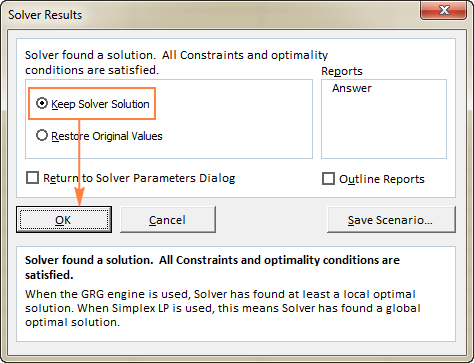
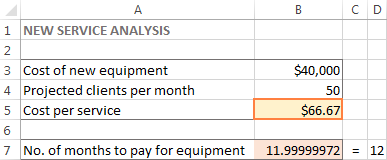
Прозор Резултат решавања ће се затворити и решење ће се појавити на радном листу одмах.
У овом примеру, 66,67 УСД се појављује у ћелији Б5, што је минимална цена по услузи која ће вам омогућити да платите нову опрему за 12 месеци, под условом да има најмање 50 клијената по месец:
Савети:
- Ако Екцел Солвер предуго обрађује одређени проблем, можете прекинути процес притиском на Есц тастер. Екцел ће поново израчунати радни лист са последњим вредностима пронађеним за ћелије Променљива .
- Да бисте добили више детаља о решеном проблему, кликните на тип извештаја у пољу Извештаји , а затим кликните на ОК . Извештај ће бити креиран на новом радном листу:
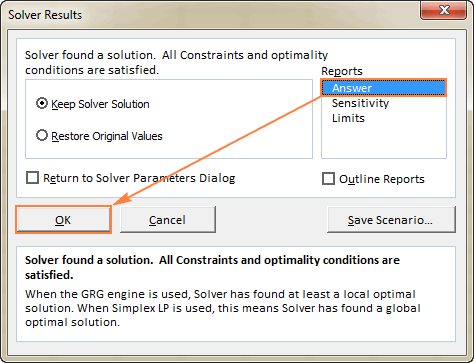
Сада када имате основну идеју о томе како да користите Солвер у Екцел-у, хајде да ближе погледамо неколико још примера који би вам могли помоћи да стекнете више разумевања.
Примери Екцел Солвера
У наставку ћете наћи још два примера коришћења додатка Екцел Солвер. Прво ћемо пронаћи решење за добро познату слагалицу, а затим решити стварни проблем линеарног програмирања.
Екцел Солвер пример 1 (магични квадрат)
Иверујте да су сви упознати са загонеткама „магични квадрат“ у којима морате да ставите скуп бројева у квадрат тако да сви редови, колоне и дијагонале буду збир одређеног броја.
На пример, да ли знате решење за квадрат 3к3 који садржи бројеве од 1 до 9 где сваки ред, колона и дијагонала дају 15?
Вероватно није велика ствар решити ову загонетку покушајима и грешкама, али кладим се да ће Решавач пронаћи решење брже. Наш део посла је да правилно дефинишемо проблем.
За почетак унесите бројеве од 1 до 9 у табелу која се састоји од 3 реда и 3 колоне. Екцел Солверу заправо нису потребни ти бројеви, али ће нам помоћи да визуелизујемо проблем. Оно што је додатку за Екцел Солвер заиста потребно су формуле СУМ које збрајају сваки ред, колону и 2 дијагонале:
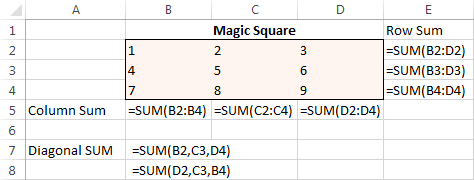
Са свим формулама на месту, покрените Солвер и подесите следеће параметре:
- Сет Циљ . У овом примеру, не морамо да постављамо никакав циљ, па оставите овај оквир празан.
- Променљиве ћелије . Желимо да попунимо бројеве у ћелијама Б2 до Д4, па изаберите опсег Б2:Д4.
- Ограничења . Следећи услови би требало да буду испуњени:
- $Б$2:$Д$4 = АллДифферент - све ћелије променљиве треба да садрже различите вредности.
- $Б$2:$Д$4 = цео број - све ћелија променљиве треба да буду цели бројеви.
- $Б$5:$Д$5 = 15 - збир вредности у свакојколона треба да буде 15.
- $Е$2:$Е$4 = 15 - збир вредности у сваком реду треба да буде 15.
- $Б$7:$Б$8 = 15 - збир од обе дијагонале треба да буде 15.
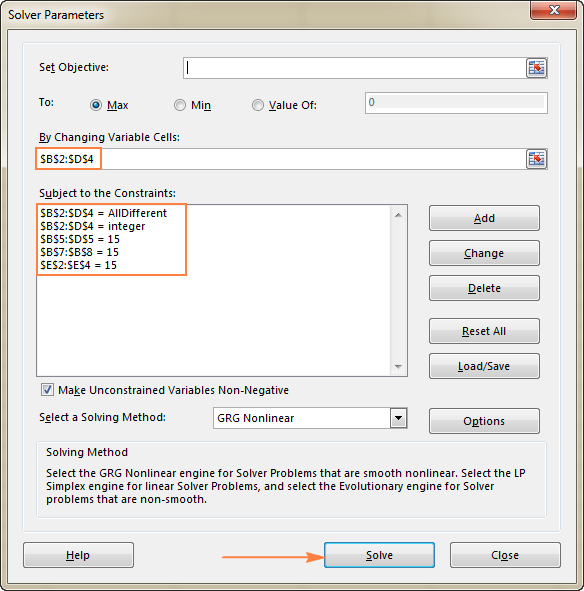
Коначно, кликните на дугме Реши и решење је ту!
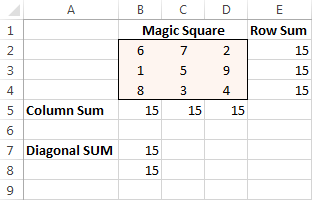
Екцел Солвер пример 2 (проблем линеарног програмирања)
Ово је пример једноставног проблема оптимизације транспорта са линеарним циљем. Сложеније моделе оптимизације ове врсте користе многе компаније да уштеде хиљаде долара сваке године.
Проблем : Желите да минимизирате трошкове испоруке робе из 2 различита складишта у 4 различита купаца. Свако складиште има ограничену понуду и сваки купац има одређену потражњу.
Циљ : Минимизирати укупне трошкове испоруке, не прелазећи количину доступну у сваком складишту и задовољити потражњу сваког купца .
Изворни подаци
Ево како изгледа наш проблем оптимизације транспорта:
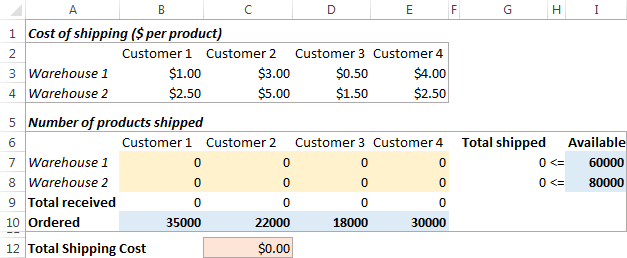
Формулисање модела
За да дефинишемо наш проблем линеарног програмирања за Екцел Солвер, хајде да одговоримо на 3 главна питања:
- Које одлуке треба донети? Желимо да израчунамо оптималну количину робе за испоруку сваком купцу из сваког складишта. Ово су Вариабле ћелије (Б7:Е8).
- Која су ограничења? Залихе доступне у сваком складишту (И7:И8) не могу се прекорачити, а

