I den här handledningen lär du dig vad en Excel-arrayformel är, hur du anger den korrekt i dina kalkylblad och hur du använder arraykonstanter och arrayfunktioner.

Arrayformler i Excel är ett extremt kraftfullt verktyg och ett av de svåraste att behärska. En enda arrayformel kan utföra flera beräkningar och ersätta tusentals vanliga formler. Ändå har 90 % av användarna aldrig använt arrayfunktioner i sina kalkylblad, helt enkelt för att de är rädda för att lära sig dem.

Mönsterformler är faktiskt en av de mest förvirrande Excel-funktionerna att lära sig. Syftet med den här handledningen är att göra inlärningskurvan så enkel och smidig som möjligt.

Vad är en array i Excel?

Innan vi börjar med array-funktioner och formler ska vi först reda ut vad termen "array" betyder. En array är i princip en samling objekt. Elementen kan vara text eller siffror och de kan finnas i en enda rad eller kolumn, eller i flera rader och kolumner.

Om du t.ex. lägger in din veckolista i ett Excel-format skulle den se ut på följande sätt:

{"Mjölk", "Ägg", "Smör", "Majsflingor"}

Om du sedan markerar cellerna A1 till D1, skriver in ovanstående matris med ett likhetstecken (=) i formellfältet och trycker på CTRL + SHIFT + ENTER får du följande resultat:

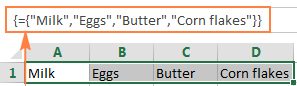
Vad du just har gjort är att skapa en endimensionell horisontell array. Inget hemskt hittills, eller hur?

Vad är en matrisformel i Excel?

Skillnaden mellan en matrisformel och en vanlig formel är att en matrisformel bearbetar flera värden i stället för bara ett. Med andra ord utvärderar en matrisformel i Excel alla enskilda värden i en matris och utför flera beräkningar på ett eller flera objekt enligt de villkor som uttrycks i formeln.

En arrayformel kan inte bara hantera flera värden samtidigt, den kan också returnera flera värden samtidigt. Det resultat som returneras av en arrayformel är alltså också en array.

Arrayformler finns i alla versioner av Excel 2019, Excel 2016, Excel 2013, Excel 2010, Excel 2007 och lägre.

Och nu verkar det vara rätt tid för dig att skapa din första arrayformel.

Enkelt exempel på en Excel-formel för matriser

Antag att du har några artiklar i kolumn B, deras priser i kolumn C och att du vill beräkna totalsumman av all försäljning.

Naturligtvis finns det inget som hindrar dig från att beräkna subtotaler i varje rad först med något så enkelt som =B2*C2 och summera sedan dessa värden:

Med en matrisformel kan du dock slippa dessa extra tangenttryckningar eftersom Excel lagrar mellanliggande resultat i minnet i stället för i en extra kolumn. Allt som krävs är en enda matrisformel och två snabba steg:

1. Välj en tom cell och skriv in följande formel i den:

   =SUM(B2:B6*C2:C6)

2. Tryck på tangentbordsgenvägen CTRL + SHIFT + ENTER för att slutföra matrisformeln.

   När du gör detta omger Microsoft Excel formeln med {slingrande hängslen}, vilket är en visuell indikation på att det rör sig om en matrisformel.

   Formeln multiplicerar värdena i varje enskild rad i den angivna matrisen (cellerna B2 till C6), adderar delsummorna och ger ut den totala summan:

   

Det här enkla exemplet visar hur kraftfull en arrayformel kan vara. När du arbetar med hundratals och tusentals rader med data kan du tänka på hur mycket tid du kan spara genom att skriva in en arrayformel i en enda cell.

Varför använda matrisformler i Excel?

Excel-arrayformler är det bästa verktyget för att utföra sofistikerade beräkningar och komplexa uppgifter. En enda arrayformel kan bokstavligen ersätta hundratals vanliga formler. Arrayformler är mycket bra för uppgifter som t.ex:

• Summera tal som uppfyller vissa villkor, till exempel summera N största eller minsta värden i ett intervall.
• Summera varannan rad, eller var N:e rad eller kolumn, som i det här exemplet.
• Räkna antalet av alla eller vissa tecken i ett visst intervall. Här är en formel för en array som räknar alla tecken och en annan som räknar vissa tecken.

Hur du anger en matrisformel i Excel (Ctrl + Shift + Enter)

Som du redan vet är kombinationen av de tre tangenterna CTRL + SHIFT + ENTER en magisk kombination som förvandlar en vanlig formel till en matrisformel.

När du skriver in en matrisformel i Excel finns det fyra viktiga saker att tänka på:

1. När du har skrivit färdigt formeln och samtidigt tryckt på tangenterna CTRL SHIFT ENTER, omsluter Excel automatiskt formeln mellan {slingrande hakar}. När du markerar en sådan cell(er) kan du se hakar i formellfältet, vilket ger dig en ledtråd om att det finns en matrisformel där.
2. Det går inte att skriva in hängslen runt en formel manuellt, utan du måste trycka på genvägen Ctrl+Shift+Enter för att slutföra en matrisformel.
3. Varje gång du redigerar en matrisformel försvinner hängslen och du måste trycka på Ctrl+Shift+Enter igen för att spara ändringarna.
4. Om du glömmer att trycka på Ctrl+Shift+Enter kommer formeln att bete sig som en vanlig formel och endast behandla de första värdena i de angivna matriserna.

Eftersom alla Excel-matrisformler kräver att du trycker på Ctrl + Shift + Enter kallas de ibland för CSE-formler .

Använd F9-tangenten för att utvärdera delar av en matrisformel.

När du arbetar med matrisformler i Excel kan du observera hur de beräknar och lagrar sina objekt (interna matriser) för att visa det slutresultat som visas i en cell. För att göra detta markerar du ett eller flera argument inom en funktions parentes och trycker sedan på tangenten F9. För att lämna formelevalueringsläget trycker du på Esc-tangenten.

I exemplet ovan väljer du B2:B6*C2:C6, trycker på F9 och får följande resultat om du vill se delsummorna för alla produkter.

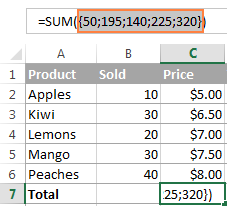
Observera att du måste välja en del av formeln innan du trycker på F9, annars kommer F9-tangenten helt enkelt att ersätta formeln med de beräknade värdena.

Formler för matriser med en och flera celler i Excel

En Excel-arrayformel kan ge ett resultat i en enda cell eller i flera celler. En arrayformel som anges i ett antal celler kallas för en formel med flera celler En matrisformel som finns i en enda cell kallas för en formel för enstaka celler .

Det finns några Excel-arrayfunktioner som är utformade för att återge arrayer med flera celler, t.ex. TRANSPOSE, TREND, FREKVENS, LINEST osv.

Andra funktioner, t.ex. SUM, AVERAGE, AGGREGATE, MAX, MIN, kan beräkna matrisuttryck när de skrivs in i en enda cell med hjälp av Ctrl + Shift + Enter .

Följande exempel visar hur du använder en formel för en array med en och flera celler.

Exempel 1. En formel för ett matris med en enda cell

Anta att du har två kolumner med antalet sålda artiklar under två olika månader, låt oss säga kolumnerna B och C, och att du vill hitta den maximala försäljningsökningen.

Normalt sett skulle du lägga till ytterligare en kolumn, till exempel kolumn D, som beräknar försäljningsförändringen för varje produkt med hjälp av en formel av typen =C2-B2 , och sedan hitta det högsta värdet i den extra kolumnen =MAX(D:D) .

En matrisformel behöver ingen extra kolumn eftersom den lagrar mellanliggande resultat perfekt i minnet. Du skriver alltså bara in följande formel och trycker på Ctrl + Shift + Enter :

=MAX(C2:C6-B2:B6)

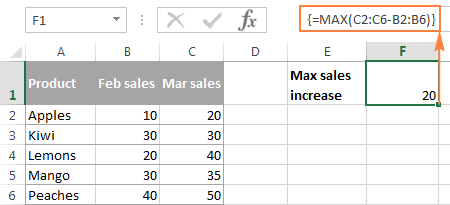
Exempel 2. En formel för en matris med flera celler i Excel

Anta att du måste betala 10 % skatt för varje försäljning i det tidigare exemplet med SUMM och att du vill beräkna skattebeloppet för varje produkt med en formel.

Markera intervallet med tomma celler, till exempel D2:D6, och ange följande formel i formellfältet:

=B2:B6 * C2:C6 * 0,1

När du trycker på Ctrl + Shift + Enter placerar Excel en instans av din matrisformel i varje cell i det markerade intervallet och du får följande resultat:

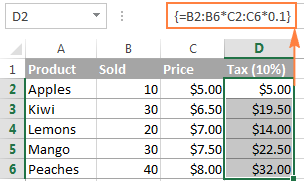
Exempel 3. Använda en Excel-arrayfunktion för att returnera en array med flera celler

Som redan nämnts tillhandahåller Microsoft Excel några så kallade "array-funktioner" som är speciellt utformade för att arbeta med arrayer med flera celler. TRANSPOSE är en sådan funktion och vi kommer att använda den för att transponera tabellen ovan, dvs. omvandla rader till kolumner.

1. Markera ett tomt område med celler där du vill skriva ut den omvända tabellen. Eftersom vi konverterar rader till kolumner ska du välja lika många rader och kolumner som källtabellen har kolumner respektive rader. I det här exemplet väljer vi 6 kolumner och 4 rader.
2. Tryck på F2 för att gå in i redigeringsläget.
3. Skriv in formeln och tryck på Ctrl + Shift + Enter .

I vårt exempel är formeln:

=TRANSPOSE($A$1:$D$6)

Resultatet kommer att se ut ungefär så här:

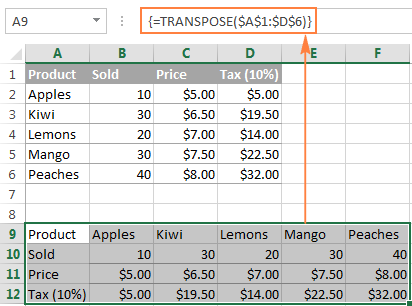
Så här använder du TRANSPOSERA som en CSE-arrayformel i Excel 2019 och tidigare. I Dynamic Array Excel fungerar detta även som en vanlig formel. Om du vill lära dig andra sätt att transponera i Excel kan du läsa den här handledningen: Hur du byter kolumner och rader i Excel.

Hur man arbetar med formler för matriser med flera celler

När du arbetar med formler för matriser med flera celler i Excel ska du följa de här reglerna för att få rätt resultat:

1. Markera det område av celler där du vill visa resultaten. före ange formeln.
2. Till ta bort en formel för en matris med flera celler, antingen markera alla celler som innehåller formeln och tryck på DELETE , eller markera hela formeln i formellfältet, tryck på DELETE och tryck sedan på Ctrl + Shift + Enter .
3. Du kan inte redigera eller flytta innehållet i en enskild cell i en matrisformel, och du kan inte heller infoga nya celler i eller ta bort befintliga celler från en matrisformel med flera celler. När du försöker göra det här kommer Microsoft Excel att visa varningen " Du kan inte ändra en del av en matris ".
4. Till krympa en matrisformel, dvs. för att tillämpa den på färre celler, måste du först ta bort den befintliga formeln och sedan skriva in en ny.
5. Till expandera en matrisformel, dvs. tillämpa den på fler celler, markera alla celler som innehåller den aktuella formeln plus tomma celler där du vill ha den, tryck på F2 för att växla till redigeringsläge, justera referenserna i formeln och tryck på Ctrl + Shift + Enter för att uppdatera den.
6. Du kan inte använda formler för matriser med flera celler i Excel-tabeller.
7. Du bör ange en formel för en matris med flera celler i ett cellområde av samma storlek som den matris som formeln returnerar. Om din Excel-matrisformel producerar en matris som är större än det valda området visas inte de överskjutande värdena på arbetsbladet. Om en matris som formeln returnerar är mindre än det valda området visas #N/A-fel i extra celler.

Om formeln kan ge en matris med ett variabelt antal element, ange det i ett intervall som är lika med eller större än den maximala matris som formeln ger tillbaka och omsluta formeln med IFERROR-funktionen, enligt exemplet nedan.

Konstanter för Excel-arrayer

I Microsoft Excel är en arraykonstant helt enkelt en uppsättning statiska värden. Dessa värden ändras aldrig när du kopierar en formel till andra celler eller värden.

I början av den här handledningen såg du redan ett exempel på en arraykonstant som skapats från en inköpslista. Nu ska vi se vilka andra arraytyper som finns och hur du skapar dem.

Det finns tre typer av konstanter för matriser:

1. Horisontell konstanta matris

En horisontell arraykonstant finns i en rad. Om du vill skapa en rad arraykonstant skriver du värdena separerade med kommatecken och omsluter dem med hakar, till exempel {1,2,3,4}.

Observera: När du skapar en arraykonstant bör du skriva de öppna och stängda hängslen manuellt.

Om du vill ange en horisontell matris i ett kalkylblad markerar du motsvarande antal tomma celler i en rad, skriver formeln ={1,2,3,4} i formellfältet och tryck på Ctrl + Shift + Enter . Resultatet kommer att se ut ungefär så här:

Som du ser i skärmbilden omsluter Excel en arraykonstant i en annan parentes, precis som när du skriver in en arrayformel.

2. Konstant vertikal matris

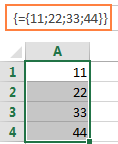
En vertikal arraykonstant finns i en kolumn. Du skapar den på samma sätt som en horisontell array med den enda skillnaden att du avgränsar posterna med semikolon, till exempel:

={11; 22; 33; 44}

3. Tvådimensionell konstant för matris

För att skapa en tvådimensionell array separerar du varje rad med ett semikolon och varje datakolumn med ett kommatecken.

={"a", "b", "c"; 1, 2, 3}

Arbeta med Excel-arraykonstanter

Arraykonstanter är en av hörnstenarna i en Excel-arrayformel. Följande information och tips kan hjälpa dig att använda dem på det mest effektiva sättet.

1. Elementen i en konstant i en matris

   En arraykonstant kan innehålla siffror, textvärden, booleska värden (TRUE och FALSE) och felvärden, separerade med kommatecken eller semikolon.

   Du kan ange ett numeriskt värde som ett heltal, en decimal eller i vetenskaplig notation. Om du använder textvärden ska de omges av dubbla citattecken (") som i alla Excel-formler.

   En arraykonstant kan inte innehålla andra arrayer, cellreferenser, intervall, datum, definierade namn, formler eller funktioner.

2. Namngivning av konstanter för matriser

   För att göra det lättare att använda en arraykonstant kan du ge den ett namn:

   • Växla till Fliken Formler> Definierade namn grupp och klicka på Definiera namn Alternativt kan du trycka på Ctrl + F3 och klicka på Ny .
   • Skriv namnet i fältet Namn
   • I Hänvisar till anger du posterna i din arraykonstant omgiven av parenteser med det föregående likhetstecknet (=). Till exempel:

     ={"Su", "Mo", "Tu", "We", "Th", "Fr", "Sa"}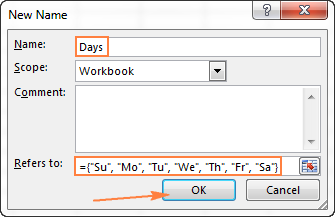

     

   • Klicka på OK för att spara den namngivna matrisen och stänga fönstret.

   Om du vill ange den namngivna konstanten i ett ark markerar du lika många celler i en rad eller kolumn som det finns objekt i matrisen, skriver matrisens namn i formellfältet före =-tecknet och trycker på Ctrl + Shift + Enter .

   Resultatet bör se ut så här:

   

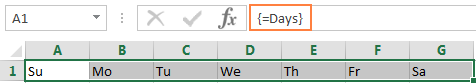
3. Förebyggande av fel

   Om din arraykonstant inte fungerar korrekt kan du kontrollera följande problem:

   • Avgränsa elementen i din arraykonstant med rätt tecken - kommatecken i horisontella arraykonstanter och semikolon i vertikala.
   • Du har valt ett antal celler som exakt motsvarar antalet objekt i din arraykonstant. Om du väljer fler celler kommer varje extra cell att ha felet #N/A. Om du väljer färre celler kommer endast en del av arrayen att infogas.

Använda konstanter i Excel-formler

Nu när du är bekant med begreppet konstanter för matriser ska vi se hur du kan använda informella matriser för att lösa praktiska uppgifter.

Exempel 1. Summa N största/småste tal i ett intervall

Du börjar med att skapa en vertikal arraykonstant som innehåller så många tal som du vill summera. Om du till exempel vill addera tre minsta eller största tal i ett intervall är arraykonstanten {1,2,3}.

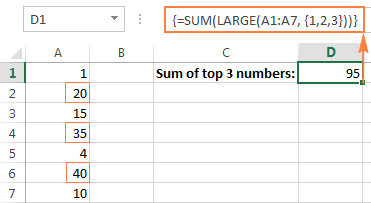
Sedan tar du antingen LARGE- eller SMALL-funktionen, anger hela cellintervallet i den första parametern och inkluderar arraykonstanten i den andra. Slutligen bäddar du in den i SUM-funktionen, så här:

Summera de tre största talen: =SUM(LARGE(range, {1,2,3}))

Summera de tre minsta talen: =SUM(SMALL(intervall, {1,2,3}))

Glöm inte att trycka på Ctrl + Shift + Enter eftersom du skriver in en arrayformel, så får du följande resultat:

På samma sätt kan du beräkna medelvärdet av N minsta eller största värden i ett intervall:

Genomsnitt av de tre högsta siffrorna: =MITTELvärde(LARGE(range, {1,2,3}))

Genomsnittet av de tre lägsta siffrorna: =MITTELvärde(SMALL(range, {1,2,3}))

Exempel 2. Arrayformel för att räkna celler med flera villkor

Antag att du har en lista över beställningar och vill veta hur många gånger en viss säljare har sålt vissa produkter.

Det enklaste sättet är att använda en COUNTIFS-formel med flera villkor. Men om du vill inkludera många produkter kan din COUNTIFS-formel bli för stor. För att göra den mer kompakt kan du använda COUNTIFS tillsammans med SUM och inkludera en arraykonstant i ett eller flera argument, till exempel:

=SUM(COUNTIFS(range1, "criteria1", range2, {"criteria1", "criteria2"}))

Den verkliga formeln kan se ut på följande sätt:

=SUM(COUNTIFS(B2:B9, "sally", C2:C9, {"äpplen", "citroner"}))

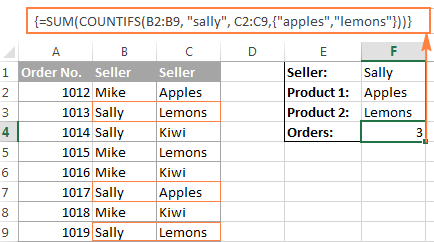
Vår exempelmatris består av endast två element eftersom målet är att demonstrera tillvägagångssättet. I dina riktiga matrisformler kan du inkludera så många element som din affärslogik kräver, förutsatt att den totala längden på formeln inte överstiger 8 192 tecken i Excel 2019-2007 (1 024 tecken i Excel 2003 och lägre) och att din dator är tillräckligt kraftfull för att bearbeta stora matriser.Se Begränsningar för matrisformler för mer information.

Och här är ett exempel på en avancerad formel för matriser som hittar summan av alla matchande värden i en tabell: SUM och VLOOKUP med en matriskonstant.

AND- och OR-operatorer i Excel-formler för matriser

En array-operator talar om för formeln hur du vill bearbeta arrayer - med AND- eller OR-logik.

• AND-operatorn är asterisk (*) som är multiplikationssymbolen och som instruerar Excel att återge TRUE om ALLA villkor är TRUE.
• OR-operatorn är plustecknet (+) och returnerar TRUE (sant) om något av villkoren i ett givet uttryck är TRUE (sant).

Array-formel med AND-operatorn

I det här exemplet hittar vi summan av försäljningen där säljaren är Mike OCH produkten är Äpplen :

=SUM((A2:A9="Mike") * (B2:B9="Äpplen") * (C2:C9))

Eller

=SUM(IF(((A2:A9="Mike") * (B2:B9="Äpplen")), (C2:C9)))

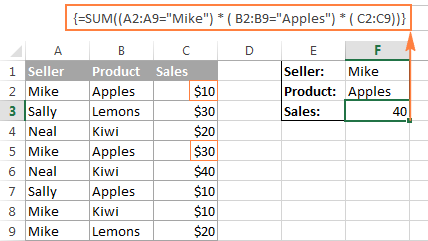
Tekniskt sett multiplicerar formeln elementen i de tre matriserna i samma positioner. De två första matriserna representeras av värdena TRUE (sant) och FALSE (falskt), som är resultatet av att A2:A9 jämförs med "Mike" och B2:B9 med "äpplen". Den tredje matrisen innehåller försäljningsnumren i intervallet C2:C9. Precis som i alla matematiska operationer omvandlar multiplikation TRUE (sant) och FALSE (falskt) till 1 respektive 0. Och eftersomMultiplicering med 0 ger alltid noll, och den resulterande matrisen har 0 om något av eller båda villkoren inte är uppfyllda. Om båda villkoren är uppfyllda hamnar motsvarande element från den tredje matrisen i den slutliga matrisen (t.ex. 1*1*C2 = 10). Resultatet av multiplikationen är alltså denna matris: {10;0;0;0;0;30;0;0;0;0;0;0}. Slutligen adderar SUM-funktionen matrisens element och ger ett resultat på 40.

Excel-formel med OR-operatorn

Följande formel med OR-operatorn (+) summerar all försäljning där säljaren är Mike OR produkten är Äpplen:

=SUM(IF(((A2:A9="Mike") + (B2:B9="Äpplen")), (C2:C9)))

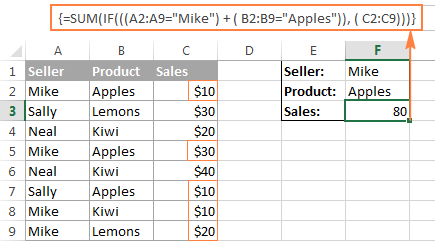
I den här formeln adderar du elementen i de två första matriserna (som är de villkor som du vill testa) och får TRUE (>0) om minst ett villkor är TRUE och FALSE (0) om alla villkor är FALSE. Sedan kontrollerar IF om resultatet av additionen är större än 0 och om det är så, adderar SUM ett motsvarande element i den tredje matrisen (C2:C9).

Tips: I moderna versioner av Excel finns det inget behov av att använda en matrisformel för den här typen av uppgifter - en enkel SUMIFS-formel hanterar dem perfekt. Men AND- och OR-operatörerna i matrisformler kan visa sig vara till hjälp i mer komplexa scenarier, för att inte tala om en mycket bra sinnesgymnastik : )

Dubbel unär operatör i Excel-formler för matriser

Om du någonsin har arbetat med matrisformler i Excel är det troligt att du har stött på några formler som innehåller ett dubbelstreck (--) och du kanske har undrat vad det används till.

Ett dubbelt streck, som tekniskt sett kallas för dubbel unär operatör, används för att konvertera icke-numeriska boolska värden (TRUE/FALSE) som returneras av vissa uttryck till 1 och 0 som en arrayfunktion kan förstå.

Följande exempel kommer förhoppningsvis att göra det lättare att förstå: Anta att du har en lista med datum i kolumn A och vill veta hur många datum som inträffar i januari, oavsett år.

Följande formel fungerar utmärkt:

=SUM(--(MONTH(A2:A10)=1))

Eftersom det här är en Excel-formel för matriser, kom ihåg att trycka på Ctrl + Shift + Enter för att slutföra formeln.

Om du är intresserad av någon annan månad ersätter du 1 med ett motsvarande nummer. 2 står till exempel för februari, 3 för mars och så vidare. För att göra formeln mer flexibel kan du ange månadens nummer i en cell, som i skärmbilden:

Nu ska vi analysera hur formeln för matrisen fungerar. Funktionen MONTH returnerar månaden för varje datum i cellerna A2 till A10 som representeras av ett löpnummer, vilket ger matrisen {2;1;4;2;12;1;2;12;1}.

Därefter jämförs varje element i matrisen med värdet i cell D1, som i det här exemplet är nummer 1. Resultatet av jämförelsen är en matris med booleska värden TRUE och FALSE. Som du minns kan du välja en viss del av en matrisformel och trycka på F9 för att se vad den delen motsvarar:

Slutligen måste du omvandla dessa booleska värden till 1 och 0 som SUMM-funktionen kan förstå. Och det är detta som den dubbla unära operatorn behövs för. Den första unära operatorn omvandlar TRUE/FALSE till -1/0. Den andra unära operatorn negerar värdena, dvs. vänder på tecknet, och omvandlar dem till +1 och 0, som de flesta Excel-funktioner kan förstå och arbeta med. Om du tar bort den dubbla unära operatornfrån formeln ovan, kommer det inte att fungera.

Jag hoppas att denna korta handledning har varit till hjälp på din väg till att behärska Excel-arrayformler. Nästa vecka fortsätter vi med Excel-arrayer genom att fokusera på avancerade formelexempel. Håll dig uppdaterad och tack för att du läste!